1. Putting the Two Ways to Thermodynamics in Context
- Top of page
- Abstract
- 1. Putting the Two Ways to Thermodynamics in Context
- 2. On the Third Way: the Unification between Mechanics and Thermodynamics
- Acknowledgements
- References
In the 1820s, the French engineer Sadi Carnot found a precise law ruling the transformations of caloric transfer into mechanical work based on his inquiries into the relationship between mechanical and thermal processes in thermal engines. In the 1850s, the Scottish natural philosopher William Thomson tried to integrate a principle of conservation of energy with Carnot's theory of thermal engines. Moreover, he tried a cosmological extrapolation, and imagined a Universe running towards its death because of the dissipation of energy, both in spontaneous transformations and in thermal engines. Later, Rudolf Clausius abandoned Carnot's idea that heat had to be conserved, and put forward different versions of a fundamental law which was soon known as the second law of thermodynamics. He associated the law with a new physical concept, ‘the content of transformation,’ which had to be conserved in ideal thermal engines. Subsequently he introduced the concept of entropy, a state function whose value could not decrease.4.
In the 1860s, James Clerk Maxwell made use of statistical concepts in order to obtain the distribution of molecular velocities in a gas. In the 1870s, Ludwig Boltzmann attempted to develop a statistical theory of entropy. In these instances the novelty was the introduction of probability into physics: probability became an intrinsic feature of physical systems with a huge number of elementary components. Boltzmann tried to go far beyond Maxwell: he was not satisfied with the description of the state of equilibrium. He looked for a law which could also describe the evolution towards the equilibrium. He was strongly influenced by Darwin's researches on biological evolution. He imagined a law of evolution which did not involve the single molecule, or its individual path, but the whole system of molecules.5.
Boltzmann introduced probability into physics in a new fundamental way: not in order to attain some useful approximation but as an intrinsic property of the system. Probability gained a new epistemic role, not so different from the role of the recently stated principle of energy conservation. In Boltzmann's representation, the motion of molecules involved both continuous paths and discrete collisions. In some way, two different traditions were at stake: Newtonian laws of motion, on the one hand, and Cartesian (and Leibnitzian) laws of conservation, on the other hand. The behaviour and the evolution of the whole system required a complex interplay between these traditions. Beside the conceptual tension between continuous and discrete representations of physical events, other tensions or dichotomies were involved: macroscopic versus microscopic representations, reversible versus irreversible behaviour of physical systems, and determinism versus probability.6.
Both Maxwell and Boltzmann pointed out the statistical meaning of the second law: that law could be violated locally, even though it preserved its validity on a large scale of space and time. The new, complex interplay between Mechanics and Thermodynamics raised a widespread debate, well known to historians of physics. Boltzmann's specific theoretical approach did not prevent him from exploring new conceptual horizons. In 1886, he imagined a body moving in a definite direction with a given velocity as an ‘infinitely improbable configuration of energy.’ According to that view, ‘visible motion behaves like heat of infinitely high temperature,’ which ‘can be completely transformed into work.’ Although he had tried to derive Thermodynamics from a new alliance between Mechanics and probability, he acknowledged that, in this case, Mechanics could be interpreted as an extreme instance of Thermodynamics.7.
A different theoretical way was undertaken by the Scottish engineer William J. M. Rankine, and by the French engineer Robert Massieu: they tried a highly abstract, mathematical interpretation of Thermodynamics. If the role of the former in the history of Thermodynamics has been acknowledged by contemporary physicists and by present-day historians, the latter is definitely less known. Rankine put forward an abstract re-interpretation of Thermodynamics, and tried to extend the new formal framework to all fields of physics giving rise to a wide design of unification he labelled ‘Energetics.’ Massieu was a mining engineer and professor at Rennes university: he was able to demonstrate that some mechanical and thermal properties of physical and chemical systems could be derived from two ‘characteristic functions.’8.
Josiah W. Gibbs and Hermann von Helmholtz developed that abstract re-interpretation of Thermodynamics, and exploited the structural analogy between Mechanics and Thermodynamics. Between 1875 and 1879, in the series of papers under the common title ‘On the Equilibrium of the Heterogeneous Substances,’ Gibbs showed that Massieu's functions played the role of potentials. In particular, the two functions were no more than the thermodynamic potential at constant temperature and volume, and the thermodynamic potential at constant temperature and pressure. In 1883 Helmholtz put forward the concept of ‘free energy’: it was the variation in free energy, rather than the whole delivery of heat, which allowed scientists to predict the actual direction of chemical transformations (Gibbs, 1875–1878, pp. 55–56, 62–69, 87–93, 115–116, 138, 184–185, 209–214, 354–355, Helmholtz, 1882, p. 960).
Maxwell, Boltzmann, Rankine, Gibbs, Helmholtz, … may all be described as natural philosophers and physicists. The field of knowledge we call physics developed from a historical process that culminated in the last decades of the 19th century and spawned the scholarly professional appointment of physicists. If the emergence of physics as a definite academic discipline was a heritage of the late 19th century, the emergence of theoretical physics was the most original outcome of that process. The fruitful alliance between the tradition of mathematical physics and the most speculative side of the tradition of natural philosophy was perhaps the most distinctive feature of late 19th century theoretical physics.9.
To describe what theoretical physics really was in that time-period is a very demanding task, because it involved both intellectual and institutional elements. I confine myself only to singling out some distinctive features, in order to better understand the context wherein Duhem undertook his scientific practice. The hallmark of late 19th-century theoretical physics was the awareness that the alliance between the mathematical language and the experimental practice celebrated by Galileo must be updated. Besides ‘definite demonstrations' and ‘sound experiments' there was a third component, which we could label conceptual or theoretical: it dealt with principles, models and patterns of explanation. That conceptual component, neither formal nor empirical, was looked upon as a fundamental component of scientific practice. Different theories could share the same mathematical framework and refer to the same kind of experiments: the difference among them could be found just at the conceptual level. Conversely, a given set of phenomena could be consistently described by different theories making reference to different conceptual models.10.
Moreover, the emergence of theoretical physics corresponded to a new sensitivity to meta-theoretical issues: we find explicit designs of unification, and explicit methodological remarks, as well as explicit questioning of the foundations of physics. At this time, all these cogitations were looked upon as intrinsic aspects of scientific practice. Scientists did not entrust philosophers with reflections on aims and methods of science: meta-theoretical remarks began to emerge from inside science, rather than being addressed to science from the outside.11.
Even though the academic recognition of theoretical physics was first achieved in German speaking countries, theoretical physics as an actual new practice in physics also appeared in France, the UK and then in Italy. We can mention Duhem and Henri Poincaré in France, Heinrich Hertz, Max Planck and Boltzmann in German speaking countries, Joseph John Thomson and Joseph Larmor in the UK, and Vito Volterra in Italy. Some of them had been trained as mathematicians; others were engineers. From the academic point of view, Poincaré was a mathematician. Duhem considered himself a physicist and mathematician: after the rejection of his first doctoral dissertation, the new one was accepted in the section of mathematics, and his physics was appreciated by mathematicians rather than by physicists. J. J. Thomson and Larmor had passed the highly selective Cambridge Mathematical Tripos, even though J. J. Thomson had gained his first degree as an engineer. Volterra was a mathematician. We cannot forget that, among the first physicists who built up theoretical thermodynamics, Rankine and Massieu had been trained as engineers, and held chairs of engineering in Scotland and France respectively. Gibbs had also been trained as an engineer in the USA, before undertaking his scientific specialization in Europe.
There are many instances of how physics' horizons began to widen in the mid to late 19th century. An early instance was offered by Rankine's abstract generalization of Thermodynamics. In the last decades of the century, we find Larmor and the theoretical and meta-theoretical role played by invisible entities like aether. Poincaré put forward the legitimate use of a plurality of theories in the interpretation of a given set of phenomena. We also find Duhem and the subtle interplay between mathematical, empirical, conceptual, historical and methodological aspects. What all these physicists had in common was a sort of two-fold attitude towards their scientific practice: there was an original combination of confidence and disenchantment with regard to science (Poincaré, 1889, pp. II, III, and 2; Boltzmann, 1890, in Boltzmann, 1974, pp. 33 and 35–36; Poincaré, 1890, pp. VIII, and XIV–XV; Poincaré, 1892, p. XIV; Larmor, 1897, pp. 207 and 215).
With regard to meta-theoretical debates, two different models of scientific knowledge were at stake. On the one hand, we find the attempt to go beyond the shield of visible phenomena, in order to catch their true microscopic nature. On the other hand, we find only mathematical representations, without any attempt to pursue subtler explanations. Those with an interest in the first approach include the Britons Larmor, J. J. Thomson, George F. FitzGerald and Oliver Lodge, but also Hendrik A. Lorentz and Boltzmann favoured this model. Those scholars who focused on mathematical representation include Gustav Kirchhoff, Ernst Mach, and the energetists Georg Helm and Wilhelm Ostwald. Then there were some who swung between the two approaches such as Hertz and then Planck who were following in the footsteps of Rankine, Maxwell, Clausius and Helmholtz.12. Poincaré looked on the two complementary attitudes with Olympic detachment. Boltzmann, Poincaré and Duhem managed to clearly describe the two meta-theoretical attitudes: explanations by means of specific mechanical models, and descriptions in terms of a formal language. Although Duhem spoke out against the mechanical models used by British physicists, the role of theory and meta-theory was so important in his actual scientific practise that we cannot put him beside Mach, Helm or Ostwald without some specifications on Mechanism and Energetism.
Duhem gave the label energetism the meaning of generalized Thermodynamics, rather than the meaning of a world-view or general meta-theoretical commitment in favour of the concept of energy. We find a remarkable conceptual distance between Duhem and some upholders of energetics like Helm and Ostwald. If Duhem developed a sophisticated mathematical theory of thermodynamics, the latter insisted on the principle of the conservation of energy as the sole foundation of physics. In particular, Ostwald developed a physical world-view wherein ‘the concept of matter, which has become indefinite and contradictory, has to be replaced by the concept of energy.’ In no way can the name of Duhem be associated with that kind of energetism.13.
With regard to the label mechanism, Duhem did not appreciate the mechanical models, and relied only on the expressive power of Analytic Mechanics. He tried to build up a sophisticated abstract Mechanics, quite different from the mechanical models of British physicists. His mechanism was a sort of structural mechanism, which he labelled Energetics. It was a very general theory similar to Rankine's Energetics: it was a generalized Mechanics as well as a generalized Thermodynamics.
In Duhem's conception of science we find meaningful analogies with Boltmann's historical and evolutionary conceptions, which is surprising considering that Boltzmann's route to Thermodynamics was through discontinuous and microscopic mechanical models. Duhem, in contrast, aimed at an abstract generalization, wherein Mechanics of continuous media merged with Thermodynamics.14. The connection becomes easier to understand, however, if we distinguish the specific physical theories from the more general meta-theoretical commitments.
As recently pointed out by Anastasious Brenner, Duhem bound together what subsequently scholars separated, namely history and philosophy of science, or in Brenner's words, ‘analytical philosophy of science and historical epistemology.’ I find that this fact probably explains another ‘intriguing’ fact: ‘after having inspired logical empiricists,’ Duhem's ‘ideas were taken up by their critics.’15. Even though this paper does not deal with Duhem's philosophical, theological, and political commitments in a strict sense, I probably should not exempt myself from reminding the reader that these issues have been widely debated, and, frequently, contradictory appraisals have emerged. In 1941 Armand Lowinger qualified Duhem's epistemology as ‘methodological positivism,’ while in (2002), Jean-Francois Stoffel qualified Duhem as a phenomenalist, after having carefully explained the difference between ‘phenomenism’ and ‘phenomenalism,’ and concluded that ‘he was realist in his heart, but phenomenalist in his mind.’ In 2011, Paul Needham credited Duhem with ‘moderate realism.’16. In 1922, the neo-Thomist François Mentré published a long paper in the neo-Thomist Revue de philosophie, in order ‘to pay homage to Pierre Duhem,’ but qualified Duhem's philosophy as ‘disappointing’ and ‘ambiguous’: although quite sophisticated and essentially correct, ‘his religious philosophy’ was essentially ‘defensive.’ It is not strange that, in 1979, Harry W. Paul remarked that, ‘[a]lthough Duhem is usually classified as a Thomist, his views were savagely contested by the hard-line Thomists,’ who could not find in Duhem ‘the aggressive philosophy needed for modern Catholicism.’ If in 1985, Roberto Maiocchi found that Duhem was isolated because of his ‘intermediate position between neo-Thomism and modernism,’ in 1987, the physicist and historian of physics Stanley Jaki labelled Duhem a naive neo-Thomist: in his words, ‘Duhem’s Thomism was that of a passionately independent amateur.’17.
2. On the Third Way: the Unification between Mechanics and Thermodynamics
- Top of page
- Abstract
- 1. Putting the Two Ways to Thermodynamics in Context
- 2. On the Third Way: the Unification between Mechanics and Thermodynamics
- Acknowledgements
- References
It was in 1886 that Duhem published Le potentiel thermodynamique et ses applications à la mécanique chimique et à la théorie des phénomènes électriques. The content of the book corresponded to the doctoral dissertation he had submitted to the faculty late in 1884, before achieving aggregation in physics. This was an unusual procedure, but the faculty let the talented student present his dissertation, which was however rejected because of his unprecedented approach to theoretical thermodynamics, and its criticism of Marcelin Berthelot's chemical theories.18.
In the ‘Introduction,’ Duhem remarked that ordinary mechanics could not solve problems concerning chemical equilibrium, even though the latter exhibited ‘several analogies with equilibrium problems in statics.’ He trusted in the mathematical structures of Analytic Mechanics: ‘les physiciens’ should have made use of procedures similar to those used by ‘les mécaniciens’ in the context of statics. Duhem was committed to bridging the gap between physics and chemistry: he was looking for a generalization of the principles already developed in the context of rational mechanics, in particular ‘the principle of virtual velocities and Lagrange's theorem.’ With this in mind he used his knowledge of history and historical reconstructions of physics to draw on the theoretical contributions to thermodynamics and thermo-chemistry put forward by Berthelot, August F. Horstmann, and John W. Strutt (Lord Rayleigh) in the 1870s. He mentioned, in particular, Massieu, who had put forward two ‘characteristic functions' H and H′ endowed with a remarkable property: quantities representing ‘physical and mechanical properties of bodies (specific heat, rate of expansion, bulk modulus, ..)’ could be deduced from them. Massieu's characteristic functions involved both energy and entropy, the most meaningful entities in thermodynamics. The first function depended on temperature and volume, and the second on temperature and pressure.19.
Then he briefly referred to the main steps of Gibbs' logical way, after having listed the two laws of equilibrium, and the two functions ψ = E(U−TS), ζ = E(U−TS) + pv, similar to Massieu's functions, which played the role of potentials. He then remarked that, in 1882, in the context of thermo-chemistry, Helmholtz had put forward ‘the distinction between two kinds of energy, the free energy … and the bound energy.’ The former could be transformed into mechanical work, but the latter could only be transformed into heat. Helmholtz's free energy F, Duhem noticed, was nothing other than Gibbs' function ψ, proportional to Messieu's ‘fonction caractéristique’H: F = E(U−TS) = ψ = −EH. Although Helmholtz's function F and Gibbs function were the same entity, Duhem noted that their applications were quite different: Helmholtz's was interested in the complex interplay among chemical, thermal, and electric effects in Volta's cells, in particular the relationship between the so-called ‘Voltaic heat' and ‘chemical heat.’20.
The first chapter of Duhem's 1886 book deals with the relationship between the mechanical and thermal properties of a physical-chemical system. His starting point was just the two principles of thermodynamics: the basic concepts were energy and entropy, the two concepts which ‘take part in the expression of thermodynamic potential.’ Then he defined a more general potential Ω = E(U−TS) + W, in which W was the mechanical work. In two specific instances, either constant volume or constant pressure, Duhem's thermodynamic potential had important consequences from the theoretical point of view as well as from the point of view of ‘applications.’ When W = 0 the potential Ω became F = E(U−TS), which was ‘Helmholtz’s free energy’ or Gibbs' ψ function. In the second case, dW = pdv = d(pv), and the potential Ω becomes Φ = E(U−TS) + pv, which is ‘just Gibbs' ζ function’ (Duhem, 1886, pp. 7–10).
The following section is definitely the most interesting from the point of view of the relationship between Mechanics and Thermodynamics. In the wake of Massieu, Duhem expressed ‘all the parameters specifying the physical and mechanical properties of a system’ in terms of the partial derivatives of Massieu's H and H′ functions, corresponding to Gibbs' ψ and ζ functions, and to Duhem's F and Φ. The function F had to be considered as a function of volume and temperature, whereas the function Φ had to be considered as a function of pressure and temperature. Entropy and volume could be expressed as derivatives of the potential Φ, as well as other mechanical and thermal properties of the system, like ‘the coefficient α of dilatation under constant pressure’ and ‘the coefficient ɛ of compressibility’ (Duhem, 1886, pp. 10–13).
In 1888 Duhem, at that time Maitre de Conférences in the Science Faculty of Lille University, was allowed to defend his new dissertation, L’aimantation par influence, at the Paris faculty of Science. He was awarded ‘Docteur ès Sciences Mathématiques’ by an academic board whose president was the mathematician Gaston Darboux, and the examiners H. Poincaré, then professor of probability calculus and mathematical physics, and Edmond Bouty, professor of physics. It is worth mentioning that Duhem's second dissertation, its title and content notwithstanding, was presented in the class of mathematics rather than in the class of physics. In the meanwhile, Duhem had published many papers on various subjects involving electromagnetism, thermo-electricity, thermo-chemistry, capillarity, osmosis, and the behaviour of vapours and chemical solutions.21.
According to a theoretical approach which borrowed names, concepts and procedures from Analytic Mechanics, Duhem followed Gibbs in stating that ‘the formal expression of the thermodynamic potential’ was the first step towards the ‘determination of the equilibrium for every system.’ Analytic Mechanics became a specific instance of a more general mechanics, wherein temperature and ‘chemical state’ were as important as pure mechanical quantities. The usual physical quantities, like shape, position and velocities, could account for the displacement of a physical system, but could not account for its transformations or ‘change of state.’ In general, for transformations involving both displacements and changes of state, the ‘internal potential’F was the suitable physical quantity for representing the conditions of equilibrium of a system. The internal potential did not have to be identified with the ‘internal energy’U, apart from the very specific case of ‘displacement without change of state’ (Duhem, 1888, pp. 5 and 10–11).
In subsequent years, Duhem developed the structural analogy between Mechanics and Thermodynamics. At the same time, he further widened the scope of the mathematical structures stemming from the tradition of Analytic Mechanics, in order to match concepts and laws stemming from Thermodynamics.
After 3 years, while he was lecturing at Lille University, he published a paper in the official revue of the Ecole Normale Supérieure, wherein he displayed what he called the ‘general equations of Thermodynamics.’ Apart from Clausius, who ‘had already devoted a paper to a systematic review on the equations of Thermodynamic,’ four scientists were credited by Duhem with having done ‘the most important researches on that subject': Massieu, Gibbs, Helmholtz, and Arthur J. von Oettingen. If Massieu had managed to derive Thermodynamics from a ‘characteristic function and its partial derivatives,’ Gibbs had managed to show that Massieu's functions ‘could play the role of potentials in the determination of the states of equilibrium’ in a given system. If Helmholtz had put forward ‘similar ideas,’ Oettingen had given ‘an exposition of Thermodynamics of remarkable generality.’ Duhem did not claim he could have done ‘better’ than the scientists quoted above, but he thought that there was real ‘interest’ in putting forward ‘the analytic development of the mechanical Theory of heat,’ making recourse to ‘very different methods.’22.
In the first section, ‘Etude thermique d’un système dont on se donne les équations d’équilibre,’ he took into account a system whose elements had the same temperature: the state of the system could be completely specified by giving its temperature ϑ and n independent parameters α, β, …, λ. The new alliance between Mechanics and Thermodynamics led to a re-interpretation of the heat exchanged dQ: heat became some kind of generalized work, or the sum of all kinds of work, mechanical as well thermal. In Duhem's hands, the new alliance led to a sort of symmetry between thermal and mechanical quantities. To the Lagrangian parameters α, β, …, λ, and ϑ he associated n + 1 functions R, R, …, R, R which played the role of generalized thermal capacities: dQ = R·dα + R·dβ + …… + R·dλ + R·dϑ (Duhem, 1891, pp. 233–234).
We find a two-fold interpretation of the functions R, R, …, R, and R. According to the mechanical interpretation, they are generalized forces; according to the thermal interpretation, they are generalized thermal capacities. The double interpretation allows us to consider the two terms in the right-hand side of the equation dU = −dQ + (1/E)dτe expressing the first principle as quantities of the same nature. From the mechanical point of view, they are both generalized works; from the thermal point of view, they are both different kinds of heat. It must be stressed that the mechanical interpretation of the term dU is a macroscopic interpretation, far from the mechanical interpretation in terms of microscopic molecular motions, which makes sense in the context of the kinetic theory of heat. The internal potential was just a generalization of the potential Duhem had introduced in 1886, namely ℱ = E[U−F(ϑ)S], where F(ϑ) was a function of temperature. Once again he reminded the reader that this generalized ‘potentiel thermodynamique interne’ corresponded to Massieu's ‘fonction caractéristique,’ Gibbs' ‘fonction de force à température constante,’ and Maxwell and Helmholtz's ‘énergie libre’ (Duhem, 1891, pp. 234–235 and 245–247; see also Duhem, 1886, pp. 9–10).
According to Duhem, ‘the mechanical determination of the system’ required firstly the specification of the function ℱ, and then the deduction of the generalized forces A, B, …, L, and Θ, and the ‘thermal coefficients' R, R, …, and R. In Duhem's representation, physical events took place in a sort of abstract hyper-space at n + 1 components: n mechanical components α, β, …, and λ, and one thermal component ϑ. The n + 1 functions A, B, …, L, and Θ, and the n + 1 functions R, R, …, R, and R depended on the whole set of parameters α, β, …, λ and ϑ. The traditional Lagrangian representation required n generalized parameters α, β, …, and λ, and a time component t. In the mechanical tradition, the parameter t played a double role: as an independent parameter, placed alongside the spatial parameters, and as basic parameter, which spatial parameters depended upon. At that stage, Duhem did not explicitly take into account time: it merely played the role of a basic implicit parameter. The role of independent parameter, on equal terms with regard to mechanical parameters, was played by the thermal parameter ϑ (Duhem, 1891, pp. 250–251).
The methods of Analytic Mechanics, or rational mechanics, were fully exploited by Duhem from the perspective of a rational thermodynamics. Had something like a crisis of mechanics ever troubled physicists at the end of the 19th century, Duhem would not have given house room to such a crisis. Since the 1880s, Duhem had pursued a new alliance between Lagrangian mechanics and the science of heat. In this he was not alone, around the same time FitzGerald, J. J. Thomson and Larmor from the UK were looking for a new alliance between Lagrangian mechanics and the science of electromagnetic phenomena. Meanwhile on main land Europe, a new alliance between Analytic Mechanics and a field theory purified by the concept of force led Hertz to a wide-ranging, although very formal, design of geometrization of physics in 1894.23.
The fact is that in the history of mechanics we must distinguish two different traditions: the tradition of mechanical models and machinery, on the one hand, and Lagrange and Hamilton's abstract mechanics, on the other. In its turn, the former could be split into different sub-traditions: the kinetic model of matter and motion, the theoretical model of forces between microscopic particles, and the theoretical model of fields of force having their place in space or the aether. As Hertz remarked in 1892, even intermediate models were at stake in the context of electromagnetic theories.24. If something like a crisis of Mechanics can be found in the late 19th century, it consisted only of a competition between the two traditions, and a debate from inside the first tradition.
Duhem's design had a double target: the unification of physics under the principles of thermodynamics, and the translation of that unified physics into a sophisticated mathematical language. The specific features of Duhem's design were quite different from the specific features of Boltzmann's: if the latter had tried to give a microscopic mechanical explanation of the macroscopic laws of Thermodynamics, Duhem assumed those macroscopic laws as a starting point. It is worth remarking that, independently from their specific theoretical models, both Boltzmann and Duhem's general attitudes towards Mechanics can be interpreted as a widening of the scope of Mechanics rather than a mere crisis of mechanics.
In 1892 Duhem submitted a long paper with the very general title ‘Commentaires aux principes de la Thermodynamique’ to the Journal de mathématiques pures et appliquées. It was the first part of a trilogy, whose second and third parts were published by the journal in 1893 and 1894 respectively. The set of three papers, when considered as a whole, was nothing less than a treatise on thermodynamics. The first paper let a wide historical and philosophical perspective emerge. The first passages clearly point out this new wide perspective, wherein the history of science appeared as a periodical series of complementary trends of innovations and applications.
Every science progresses by a series of oscillations. At times, the principles of science are discussed: the hypotheses by them presupposed, and the restrictions which they are subjected to, are analysed. Then, for a while, those principles seem well established. The efforts of theoreticians are directed towards the deduction of the consequences; the number of applications multiplies, and experimental checks increase, and become accurate.
However, this development, at first easy and fast, later becomes slower and more difficult. When the soil is unduly exploited, it becomes poorer: then some hindrances emerge, which cannot be removed by the established principles. Some contradictions cannot be solved, and some problems cannot be faced. At that moment, we must go back to the foundations of science: we must newly analyse their soundness, and precisely estimate what they can bear without giving way. After having accomplished this task, we can build up the new consequences of the theory.25.
According to Duhem, in the last ‘30 years,’ many ‘applications’ had stemmed from research into Thermodynamics: at the end of the 19th century, a deep ‘reconsideration of the principles was needed,’ even though some remarks could be looked upon as ‘more philosophical than mathematical.’ The ‘logical order’ of a physical theory could only rest upon ‘a certain number of definitions and hypotheses, which are, to some extent, arbitrary.’ In keeping with the typical open-mindedness of late-19th-century theoretical physics, Duhem acknowledged that different theoretical approaches to Thermodynamics could be ‘equally satisfactory, even more satisfactory’ than his own. There was a plurality of theories able to describe a given set of phenomena in a consistent way.26.
In the first chapter, ‘Définitions préliminaires,’ dealing with the geometrical and kinematical foundations of physics, we find the equivalence between different theoretical representations of a given set of phenomena once again. Duhem claimed that every hypothesis on the ultimate representation of matter was arbitrary, as well as the choice between the opposite theoretical models of continuity and discontinuity, even though he preferred the former.
In physics, it is impossible and at the same time useless to know the actual structure of matter. We simply try to conceive an abstract system, which can give us a representation of the properties of bodies. In order to devise this system, we are free to represent an apparently continuous body by a continuous distribution of matter in a given space, or by a discontinuous set of very small atoms. Since the first representation leads to simpler, clearer, and more sophisticated theories in every field of physics, we prefer the former to the latter. (Duhem, 1892, p. 272)
He remarked that, sometimes, some theoretical representations were unjustified from the empirical point of view. The concept of ‘an isolated body placed in an unlimited and empty space’ was one of them. Nevertheless, those representations could be useful simplifications: physics could not part with those kinds of abstraction (Duhem, 1892, p. 274).
He stressed the difference between the physical quantities that preserved their values over time and those that did not: mass and electric charge belonged to the first set, kinematical parameters to the second. If the former specified ‘the nature of the system,’ the latter specified ‘the state.’ Among state quantities Duhem distinguished those that explicitly appear in position and velocity from those that do not appear. He reserved the labels α, β, …, and λ for the former, and introduced new labels a, b, …, l for the latter: in this way he separated geometrical quantities from other quantities. In the latter subset Duhem placed temperature, a quantity, which would have played ‘a remarkable role in the present work.’ According to Duhem, temperature was not a ‘quantitative feature’ of a physical system in a strict sense: a given value of temperature could be ‘reproduced, increased and decreased,’ but temperature was not an additive quantity. Moreover, temperature could not be univocally defined: if we call it ϑ, every continuous and increasing function Θ = f(ϑ) can play the role of temperature.27.
In the second chapter, Duhem tried to clarify some basic physical concepts: closed cycles, work, kinetic and potential energies, internal energy, the additive property of work, and the principle of the conservation of energy. He stressed the status of a ‘physical hypothesis' of that principle: it was submitted to experience, and it could not be demonstrated, but only put forward by means of some physical considerations. In the third chapter he started from a complex system Σ, which was isolated in space, and could be looked upon as the composition of two ‘independent systems' S and S′. If the kinetic energy of Σ was simply the sum of the kinetic energies of S and S′, potential energy could not consist only of the sum of the potential energies of S and S′, but had to contain a term Ψ for interaction. He defined two sets of quantities derived from the potential of interaction, ‘forces’ and ‘influences,’ and called ‘actions’ the ensemble of forces and influences. The separation of actions into forces and influences followed necessarily from the separations of Lagrangian parameters into geometrical parameters and other state parameters. In the following pages, Duhem applied his definitions and remarks to the general case of a complex system Σ composed of ‘n independent systems S1, S2, …, Sn.’ Conversely, those definitions and remarks allowed Duhem to begin to draft, at least in part, the features of a ‘complex system.’28.
Heat had a relational nature: in a ‘complex isolated system, consisting of two independent systems S and S′, … one of them sends out as much heat as the other receives.’ The concept of an isolated body placed in an empty space, and sending out or receiving heat, seemed to Duhem ‘not consistent with the definition given above.’ According to Duhem, heat means exchange of heat: heat requires some sort of interaction between different bodies, or at least between a body and the surrounding aether. According to Duhem's design, his generalized Mechanics was an Analytic Thermodynamics, and ordinary mechanics should have been just one of its specific applications. In order to derive ordinary mechanics from that wide-scope Mechanics/Thermodynamics, he assumed that dQ = 0 and all ‘thermal coefficients' vanish. Since the reduced equations corresponded to Lagrange's equations of rational mechanics, the mathematical derivation seemed successfully achieved. Nevertheless, a question arose: could the physical derivation be reversed? In other words, are we sure that, when ordinary mechanics is at stake, all thermal coefficients vanish? At that stage, Duhem could not satisfactorily answer the question, and he acknowledged that further theoretical investigations were required.29.
Indeed, it is questionable whether the vanishing of the ‘thermal coefficients' and the condition dQ = 0 are equivalent statements. At the end of Duhem's 1892 paper, the nature of the relationship between Mechanics and Thermodynamics was waiting for a complete clarification.
In 1892, we find a sort of intellectual dialogue between Duhem and Poincaré in the treatise the latter devoted to Thermodynamics. Poincaré agreed with Duhem on the increasing importance of the two Principles of Thermodynamics ‘in all fields of natural philosophy,’ and on the rejection of ‘the ambitious theories full of molecular hypotheses.’ Microscopic mechanical models could not account for the second Principle: in his words, ‘mechanics collide with Clausius' theorem.’ He claimed that he would have built up ‘the whole structure of mathematical Physics only on Thermodynamics.’ The complexity of physical systems was not outside the intellectual horizon of Poincaré, for he had studied the stability of the three-body problem in celestial mechanics. He noticed that ‘the exact computation of the internal energy of a body depended on the state of external bodies': the conservation of energy in a given body called into play ‘the whole universe.’ A similar remark had to be extended to the second Principle, although it was expressed ‘by an inequality’ rather than an equality. He found that only following ‘the historical pathway,’ a scholar could understand why ‘all physicists adopted the two principles.’ Poincaré shared with Duhem the sensitivity to the historical nature of the scientific enterprise, and the ability to perform both logical and historical analyses. Moreover, he was aware of the role of ‘metaphysical’ or meta-theoretical issues besides purely ‘theoretical’ ones.30.
The following year Duhem published the second part of his Commentaire. As in the 1892 first part, the first chapter was devoted to some preliminary definitions and remarks. He faced the apparently inconsistent concept of ‘transformations which consist of a series of states of equilibrium.’ He tried to give it ‘a logic meaning,’ by resorting to the difference between geometrical parameters and state parameters. A physical system can experience a transformation without any change in its shape and position: under this condition, the transformation could be looked upon as a series of states of equilibrium. The last issue concerned ‘the concept of reversible transformation,’ one of ‘the most important and, at the same time, most problematic to be defined in Thermodynamics,’ as Duhem himself remarked. In reality, the whole 1893 Commentaire consists of a net of preliminary specifications and detailed remarks on heat, entropy, and the second Principle of Thermodynamics. There are ‘infinite reversible transformations’ leading a physical system from one state to another. For every reversible transformation, the integral 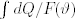 has the same value: in case of reversible cycles, the integral vanishes. It is nothing else but the entropy of the system. Once again, if we assume R = R = … = R = 0, automatically dQ = 0. This was the case of ‘classical rational Mechanics,’ wherein no reference to heat or temperature is made (Duhem, 1893, pp. 302–307, 337, 345, 355, and 357–358). The fact is that, in this case, the concept of entropy and the second Principle lost their meaning: although the mathematical derivation of Mechanics from Thermodynamics was successfully performed, the conceptual relationship between Mechanics and Thermodynamics remained a sensitive issue waiting for a satisfactory solution.
has the same value: in case of reversible cycles, the integral vanishes. It is nothing else but the entropy of the system. Once again, if we assume R = R = … = R = 0, automatically dQ = 0. This was the case of ‘classical rational Mechanics,’ wherein no reference to heat or temperature is made (Duhem, 1893, pp. 302–307, 337, 345, 355, and 357–358). The fact is that, in this case, the concept of entropy and the second Principle lost their meaning: although the mathematical derivation of Mechanics from Thermodynamics was successfully performed, the conceptual relationship between Mechanics and Thermodynamics remained a sensitive issue waiting for a satisfactory solution.
It is worth mentioning that, in the same year, Poincaré published some notes just on that conceptual relationship. In a short paper sent to a philosophical journal which had just started to be published, Revue de Métaphysique et de Morale, he compared the foundations of Mechanics and Thermodynamics. He said he would confine himself to the comparison between the ‘hindrances faced by the mechanists' and ‘experimental data.’31.
According to Poincaré, Mechanics required that ‘all phenomena are reversible’ with regard to time: in a sharper way, ‘reversibility is a necessary consequence of every mechanical hypothesis.’ The fact is that every common experience conflicted with that requirement: thermal conduction was a well-known instance of irreversibility: that ‘a cold body gives back the heat it received,’ had never been observed. In this specific case, neither ‘direct reversibility’ nor ‘indirect reversibility’ could take place after a physical system had passed ‘from a state A to a state B through a given path.’ In other words, the system cannot pass from B to A, ‘neither through the same path, nor through a different path.’ The attempts to escape this contradiction appeared ‘not sufficient' to Poincaré, Helmholtz's hypothesis of ‘hidden motions' notwithstanding (Poincaré, 1893, pp. 534–535).
The recent developments in Mechanics, inspired by the work of Poincaré himself, had shown that ‘a closed system submitted to the laws of mechanics' could repeatedly be found ‘near its initial state’ over time. On the contrary, some cosmological interpretations of the second Principle of Thermodynamics proposed that the whole universe could drift towards ‘a given final state, where it will never come back from.’ If a radical thermodynamic world-view envisioned a sort of thermal death, wherein ‘all bodies will be found at rest at the same temperature,’ according to a radical mechanical world-view, we will be able to see ‘a flow of heat from a cold body to a warm one,’ provided that we have ‘a little patience.’ The expectation that thermal irreversibility could stem from the laws of Mechanics seemed to Poincaré a non-sense: no logical procedure would have allowed us to build up a deduction wherein ‘we find reversibility at the outset, and irreversibility at the end’ (Poincaré, 1893, pp. 536–537).
In 1894, in the third part of the Commentaire, Duhem returned to the 1891 ‘general equations of Thermodynamics.’ In the first chapter, he started from a physical system defined by the set of parameters α, β, …, λ and ϑ, which seemed a step backwards when compared to the two sub-sets he had introduced in 1892. Nevertheless, soon afterwards, he tried another kind of generalization: he took into account a ‘complex system’ consisting of two ‘different and independent components' (Duhem, 1894, pp. 208–211). In the second chapter, he returned to the two sets α, β, …, λ, and a, b, …, l he had introduced in the first part of the Commentaire. The first passage of the chapter strikes the reader because of the reference to an Aristotelian conception of the word ‘motion’: not only was motion looked upon as a kinematic process, but as transformation in general. It is worth quoting Duhem's passage:
In this chapter, not only do we make use of the word motion to make reference to a change of position in space, but also to any change of state, even when it is not accompanied by a spatial displacement. Thus we have motion when the parameters a, b, …, l alone change, whereas the parameters α,β,…,λ retain constant values. In this way, the word motion is not opposed to the word rest but to the word equilibrium. (Duhem, 1894, p. 222)
Then he opened another pathway: instead of starting from general equations, and then imposing the conditions for equilibrium, he started from the equations in the case of equilibrium, and tried to generalize them to the case of non-equilibrium. From the mathematic point of view, he introduced new functions f, f, …, f, which generalized the ‘passive resistances to be overcome by the system.’ Those resistances depended on the basic parameters α, β, …, λ, ϑ, their time derivatives α′,β′,…,λ′ and the time t: from the mathematical point of view, they were ‘resistances’ in the usual mechanical sense. From this perspective, equilibrium was disturbed by some kind of generalized friction: a corresponding work f·dα + f·dβ + … + f·dλ could be associated to that kind of dissipative forces (Duhem, 1894, pp. 223–224).
According to the conceptual framework of a generalized Mechanics, he put forward a ‘fundamental hypotheses' on the passive resistances f, f, …, f: the work done by those resistances could be only null or negative. That hypothesis allowed Duhem to attain a meaningful result concerning the second Principle of Thermodynamics. He first identified the work f·dα + f·dβ + … + f·dλ with Clausius' ‘uncompensated work,’ and then he showed that no transformation involving an isolated system could therefore ‘make the entropy of the system decrease’ (Duhem, 1894, pp. 228–229).
The generalization of the concept of passive resistance, or viscosity, or friction, paved the way leading from a generalized Mechanics to the core of Thermodynamics, namely the second Principle. The second principle of Thermodynamics had therefore received a mechanical interpretation, but the interpretation was mechanical in a sense to be carefully specified. As I have already stressed, we are not dealing here with a microscopic mechanical explanation of macroscopic thermodynamic effects. We find a macroscopic mechanical re-interpretation, linked to a re-interpretation of the word ‘motion’ in the context of a renewed Aristotelian tradition.
At the end of the third Part of his Commentaire, Duhem drafted some general ‘Conclusions,’ wherein he put his approach to Mechanics and Thermodynamics into a historical perspective. In the recent history of physics, he found two different attitudes towards the relationship between Mechanics and Thermodynamics. On the one hand, most of the founding fathers of Thermodynamics had tried to transform Thermodynamics into ‘an application of Dynamics.’ They had interpreted heat as ‘the microscopic and very fast motion of particles which form ordinary bodies,’ and temperature as the ‘average living force’ corresponding to those motions. On the other hand, other physicists had tried to found Thermodynamics ‘on its own principles.’ They had not put forward any ‘hypotheses on the nature of heat'; neither had they borrowed theorems from rational Mechanics.’ What had the former attained? They had managed to successfully interpret the first Principle, namely the Principle of conservation of energy, but had failed to explain the second Principle, ‘Carnot’s Principle.’ In spite of Clausius, Boltzmann and Helmholtz's ‘daring efforts,’ the former ‘had not managed to make Carnot's principle stem from the laws of Dynamics in a satisfactory way.’ According to Duhem, the latter had had more success: Kirchhoff had shown that Clausius' preference for ‘Thermodynamics as an independent science’ could be successfully pursued (Duhem, 1894, pp. 284–285).
Duhem saw himself walking on along the third way: Thermodynamics as a generalized Mechanics, as a broad theory of transformations in a general sense.
In the present work, we have attempted to point out a third kind of relationship between Dynamics and Thermodynamics. We have transformed Dynamics into a specific instance of Thermodynamics, or better, under the name of Thermodynamics we have built up a science which encompasses within common principles every transformation of a body: both changes of place, and changes of physical qualities. (Duhem, 1894, p. 285)
His design can be looked upon as a reduction of physics to the language of Analytic Mechanics, but at the same time, as an anti-reductionist design, wherein the widening of the scope of that language was at stake. In Duhem's ‘more general science’ we can appreciate the coexistence of a mechanical approach, in the sense of Lagrange's mathematical physics, and the rejection of ‘a mechanical explication of the Universe.’32.
[This article will be continued in the next issue of Centaurus]




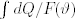 has the same value: in case of reversible cycles, the integral vanishes. It is nothing else but the entropy of the system. Once again, if we assume R = R = … = R = 0, automatically dQ = 0. This was the case of ‘classical rational Mechanics,’ wherein no reference to heat or temperature is made (
has the same value: in case of reversible cycles, the integral vanishes. It is nothing else but the entropy of the system. Once again, if we assume R = R = … = R = 0, automatically dQ = 0. This was the case of ‘classical rational Mechanics,’ wherein no reference to heat or temperature is made (