CONTENTS

Preface

Chapter I. Definitions and elementary applications

§1.1. One-parameter transformation groups

§1.2. Prolongation formulae

§1.3. Groups admissible by differential equations

§1.4. Integration and reduction of order using one-parameter groups

1.4.1. Integrating factor

1.4.2. Method of canonical variables

1.4.3. Invariant differentiation

§1.5. Defining equations

§1.6. Lie algebras

§1.7. Contact transformations

Chapter II. Integration of second-order equations admitting a two-dimensional algebra

§2.1. Consecutive reduction of order

2.1.1. An instructive example

2.1.2. Solvable Lie algebras

§2.2. The method of canonical variables

2.2.1. Changes of variables and basis in an algebra

2.2.2. Canonical form of two-dimensional algebras

2.2.3. An integration algorithm

2.2.4. An example of implementation of the algorithm

Chapter III. Group-theoretical classification of second-order equations

§3.1. Equations admitting a three-dimensional algebra

3.1.1. Classification in the complex domain

3.1.2. Classification over the reals. Isomorphism and similarity

§3.2. The general classification result

§3.3. Two remarkable classes of equations

3.3.1. The equation

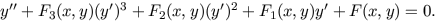
$ y'' + F_3(x, y)(y')^3 + F_2(x, y)(y')^2 + F_1(x, y)y' + F(x, y) = 0.$

Linearizability criteria

3.3.2. Equations 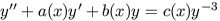$ y'' + a(x)y' +b(x)y = c(x)y^{- 3}$

Chapter IV. Ordinary differential equations with a fundamental system of solutions (following Vessiot-Guldberg-Lie)

§4.1. The main theorem

§4.2. Examples

§4.3. Projective interpretation of the Riccati equation

§4.4. Linearizable Riccati equations

Chapter V. The invariance principle in problems of mathematical physics

§5.1. Spherical functions

§5.2. A group-theoretical touch to Riemann's method

§5.3. Symmetry of fundamental solutions, or the first steps in group analysis in the space of distributions

5.3.1. Something about distributions

5.3.2. Laplace's equation

5.3.3. The heat equation

5.3.4. The wave equation

Chapter VI. Summary of results

References