A Survey of the Hysteretic Duhem Model
- Cite this article as:
- Ikhouane, F. Arch Computat Methods Eng (2017). doi:10.1007/s11831-017-9218-3
- 6 Downloads
Abstract
The Duhem model is a simulacrum of a complex and hazy reality: hysteresis. Introduced by Pierre Duhem to provide a mathematical representation of thermodynamical irreversibility, it is used to describe hysteresis in other areas of science and engineering. Our aim is to survey the relationship between the Duhem model as a mathematical representation, and hysteresis as the object of that representation.
1 Prolegomenon
Citing a reference allows the author of a scientific article to attribute work and ideas to the correct source. Nonetheless, the process of describing that work and these ideas assumes some interpretation, at least of their relative importance. In order to ensure that the interpretation is reliable, we use, whenever adequate, a quotation from the reference so that the reader has a direct access to the cited source. This direct access is even more important when the source is not easily available like Ref. [67]1 or is not written in English like Refs. [16, 17, 18, 19, 20, 21, 22] among others, in which case we provide a translation. This is our approach to the literature review of Sect. 2.
In Sects. 4–9 we proceed differently since our aim in these sections is to provide an accurate description of the results presented in the references under study. Because of the diversity of notations and nomenclature in these references, quotations may not be the best way to transmit that accurate description. Instead, we summarize the references using a unifying framework provided in Ref. [35]. The references we have chosen in Sects. 4–9 are, in our opinion, those that are relevant to the subject of this study.
Our aim in this work is also to shed light on the relationships between the concepts introduced in this paper. To this end, we use a special form of the Duhem model, the scalar semilinear one, as a case study.
2 Introduction and Literature Review
A brief history of the Duhem model The term hysteresis was coined by J. A. Ewing in 1881 to describe a specific relationship between the torsion of a magnetized wire and its polarization (although the phenomenon of hysteresis has been known and described by several authors before that date as shown in the literature review provided in Ref. [65]).
Quoting from Ewing’s paper [28]: “These curves exhibit, in a striking manner, a persistence of previous state, such as might be caused by molecular friction. The curves for the back and forth twists are irreversible, and include a wide area between them. The change of polarization lags behind the change of torsion. To this action …
However, the first in-depth study of hysteresis is due to Pierre Duhem2 in the period 1896–1902. A detailed review of Duhem’s work on hysteresis may be found in [67, Chapter IV] so that we provide here only those elements of that extensive work that are directly related to the present paper.
To understand the motivation for Duhem’s work we quote from [67, p. 306]: “take a metallic wire under strain by means of a load. We can take the length of the wire and its temperature as variables that define its state. The gravity weight P will represent the external action. At temperature T and under the load P the wire may be at equilibrium with length l. Give P infinitely small variations, the length l and temperature T will also experience infinitely small variations, and a new equilibrium may be achieved. In this last state, give the gravity weight and temperature variations equal in absolute value, but of opposite signs to the previous ones. The length l should experience a variation equal to the previous one with opposite sign. However, experimentation shows that this is not the case. In general, to the expansion of the wire corresponds a smaller contraction, and the difference lasts with time.”
This permanent deformation is the subject of a seven-memoirs research by Duhem, see Refs. [16]–[22]. In his first memoir submitted to the section of sciences of the Académie de Belgique on October 13, 1894, and reviewed by the mathematician Charles Lagrange in Ref. [44],3 Duhem writes: “The attempts to make the different kinds of permanent deformations compatible with the principles of thermodynamics have been few up till now. Only one of these attempts, due to M. Marcel Brillouin, appears to us worthy of interest.” [16, p. 3]. Duhem analyzes the work of Brillouin and concludes that it is not compatible with the principles of thermodynamics [16, p. 6] (see also [19, pp. 5–7]).
To the best of our knowledge, the first reference that called the form (5) “Duhem model” is Ref. [48] in 1993.4 Indeed, the authors of Ref. [43] attributed erroneously Duhem’s model to Madelung [63, p. 797].5
Between 1916 when P. Duhem dies and 1993 when his model of hysteresis is finally attributed to him, Duhem’s work on hysteresis does not have a relevant impact. Major references on hysteresis like Refs. [8, 12] or [56] do not cite his memoirs. Several authors propose different forms of the Duhem model without a direct reference to Duhem’s memoirs. This is the case of the Coleman and Hodgdon model of magnetic hysteresis [12], the Dahl model of friction [13], the model (5) in Ref. [3], and a generalized form of the model (5) in Ref. [43, p. 95]. In 1952, Everett cites briefly Duhem’s work as follows [24, p. 751]: “From a thermodynamic standpoint the introduction of an additional variable whose value depends on the history of the system is sufficient for a formal discussion (cf. Duhem [ref]
A general theory of physics based on a molecular interpretation was precisely what Duhem rejected. In a review of his work presented in 1913 for his application to the Académie des Sciences, Duhem writes that his “doctrine should note imitate the numerous mechanical theories proposed by physicists hitherto; to the observable properties that apparatus measure, it will not substitute hidden movements of hypothetical bodies” [67, p. 74].
In recent times, Duhem’s phenomenological approach is becoming more accepted [5, 9, 46, 52, 57]. Indeed, “hysteretic phenomena arising in structural and mechanical systems are so complicated that there has been no well-accepted mathematical model which can describe all observed hysteretic characteristics.” [52, p. 1408]. Moreover, the Preisach model which was believed to describe the constitutive behavior of magnetic hysteresis, has shown to be a phenomenological model [49, p. 2].
Several reasons are invoked for the use of Duhem’s model to describe hysteresis. On the one hand, “differential equation-based models lead to a particularly simple phenomenological description” [46, p. C8–545]. On the other hand, the “Duhem models [sic] …
There are several generalizations of the original Duhem model (5). The following generalization is proposed in [43, p. 95]: ˙x(t)=f(t,x(t),u(t),˙u(t))
Why are there different generalized forms of the Duhem model ? To answer this question we have to recall the concept of rate independence.6
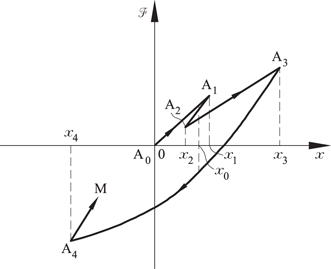
Graph “Force–displacement” with hysteresis
…
Rate independence is used by Visintin to define hysteresis :“Definition. Hysteresis = Rate Independent Memory Effect.”[64, p. 13]. However, “this definition excludes any viscous-type memory” [64, p. 13] because it leads to rate-dependent effects that increase with velocity. A definition based on rate independence assumes that “the presence of hysteresis loops is not … an essential feature of hysteresis.” [64, p. 14].
This point of view is challenged by Oh and Bernstein who consider hysteresis as a “nontrivial quasi-dc input-output closed curve” [54, p. 631] and propose a modified version of the Duhem model which can represent rate-dependent or rate-independent effects. A characterization of hysteresis systems using hysteresis loops is also addressed by Ikhouane in Ref. [35] through the concepts of consistency and strong consistency.
In light of what has been said it becomes clear that, in Ref. [64], the generalizations of Duhem’s model are done in such a way that rate independence is preserved, whilst a definition of hysteresis based on hysteresis loops in Ref. [54] is compatible with a generalized form of the Duhem model that may be rate dependent or rate independent.
Why are there different models of hysteresis? In Ref. [16] Duhem proposes his model to account for the irreversibility in the modifications of equilibria observed experimentally in magnetic hysteresis [16, Chap. IV], sulfur [17], red phosphorus [19, Chap. III], and in different processes of metallurgy [19].
Preisach [56] uses “plausible hypotheses concerning the physical mechanisms of magnetization” [49, p. 1] to elaborate a model of magnetic hysteresis. This model is also proposed and studied by Everett and co-workers [24, 25, 26, 27] who postulate “that hysteresis is to be attributed in general to the existence in a system of a very large number of independent domains, at least some of which can exhibit metastability.” [24, p. 753].
Krasnosel’skiǐ and Pokrovskiǐ point out to the issue of admissible inputs, as “it is by no means clear a priori for any concrete transducer with hysteresis, how to choose the relevant classes of admissible inputs” [43, p. 5]. This is why they introduce the concept of vibro-correctness which allows the determination of the output of a hysteresis transducer that corresponds to any continuous input, once we know the outputs that correspond to piecewise monotone continuous inputs [43, p. 6]. The models that Krasnosel’skiǐ and Pokrovskiǐ propose (ordinary play, generalized play, hysteron) are vibro-correct, although the authors acknowledge the existence of hysteresis models that may not be vibro-correct like the Duhem model.7
Hysteresis models based on a feedback interconnection between a linear system and a static nonlinearity are proposed in Ref. [55]. The authors study “hysteresis arising from a continuum of equilibria … and hysteresis arising from isolated equilibria” [55, p 101].
A review of hysteresis models is provided in Ref. [48] and a detailed study of these (and other) models may be found in Refs. [7, 10, 14, 37], [49, 64].
In light of what has been said, the diversity of hysteresis models is due to the wide range of areas to which hysteresis is concomitant, and the diversity of methods and assumptions underlying the elaboration of these models.
Note that all mathematical models of hysteresis share a common property: they model hysteresis. This fact leads us to our next question.
What is hysteresis? A description found in many papers is that hysteresis “refers to the systems that have memory, where the effects of input to the system are experienced with a certain delay in time.” [33, p. 210]. This description is misleading as it applies also to dynamic linear systems. Indeed, when the output y is related to the input u by ˙x=Ax+Bu
Mayergoyz considers hysteresis as a rate-independent phenomenon which is “consistent with existing experimental facts.” [49, p. 16]. However, “for very fast input variations, time effects become important and the given definition of rate-independent hysteresis fails.” [49, p. 16]. Also, “in the existing literature, hysteresis phenomenon is by and large linked with the formation of hysteresis loops (looping). This may be misleading and create the impression that looping is the essence of hysteresis. In this respect, the given definition of hysteresis emphasizes the fact that history dependent branching constitutes the essence of hysteresis, while looping is a particular case of branching.” [49, pp. 16–18].
Following Mayergoyz, “All rate-independent hysteresis nonlinearities fall into two general classifications: (a) hysteresis nonlinearities with local memories, and (b) hysteresis nonlinearities with nonlocal memories.” [49, pp. 17]. In a hysteresis with a local memory, the state or output at time t≥t0
In Ref. [54], Oh and Bernstein consider the generalized Duhem model ˙x=f(x,u)g(˙u)
In a PhD thesis advised by Bernstein [15], Drinčić considers systems of the form ˙x=f(x,u)
In Ref. [6] Bernstein states that “a hysteretic system must be multistable; conversely, a multistable system is hysteretic if increasing and decreasing input signals cause the state to be attracted to different equilibria that give rise to different outputs.” Multistability means that “the system must have multiple attracting equilibria for a constant input value” [6].
In Ref. [50], Morris presents six examples of hysteresis systems taken from the areas of electronics, biology, mechanics, and magnetics; hysteresis being understood as a “characteristic looping behavior of the input-output graph” [50, p. 1]. The author explains the qualitative behavior of these systems from the point of view of multistability. For “the differential equations used to model the Schmitt trigger, cellular signaling and a beam in a magnetic field” it is observed that “these systems, all possess, for a range of constant inputs, several stable equilibrium points.” [50, p. 13]. The author observes that the systems are rate dependent for high input rates.
For the play operator, the Preisach model and the Bouc-Wen model which are rate independent, “these models present a continuum of equilibrium points.” [50, p. 13]. These observations lead the author to conclude that “hysteresis is a phenomenon displayed by forced dynamical systems that have several equilibrium points; along with a time scale for the dynamics that is considerably faster than the time scale on which inputs vary.” [50, p. 13]. Morris proposes the following definition.
“A hysteretic system is one which has (1) multiple stable equilibrium points and (2) dynamics that are considerably faster than the time scale at which inputs are varied.” [50, p. 13].
In Ref. [35], Ikhouane considers a hysteresis operator “H
The author introduces two changes in time scale: (1) a linear one which is applied to a given input, and (2) a -possibly- nonlinear one which is the total variation of the original input. When the input is composed with the linear time-scale change, both the input and the output are re-scaled with respect to the total variation of the input, which provides a normalized input independent of the linear time-scale change, and a normalized output. Consistency is defined as being the convergence of the normalized outputs in the space L∞
Strong consistency is defined as the property that the limit of the normalized outputs, seen a parametrized curve, converges to a periodic orbit which characterizes the hysteresis loop.
The author does not propose a definition of hysteresis, but considers that consistency and strong consistency are properties of a class of hysteresis systems.
Aim of the paper The aim of the paper is to survey the research carried out on the Duhem model from the perspective of its hysteretic properties.
Organization of the paper Section 4 presents some results obtained in Ref. [43], namely the concept of vibro-correctness, sufficient conditions to ensure global solutions of the scalar rate independent Duhem model, and a study of the continuity of the model seen as an operator. Section 5 presents a definition of hysteresis proposed in Ref. [54] that uses a generalized form of Duhem’s model as a tool to get that formal definition. Section 6 presents the concepts of consistency and strong consistency introduced in Ref. [35]. The tools and notations of Ref. [35] are also used as a unifying framework to present the results of the present paper. Section 7 presents a characterization of the generalized Duhem model obtained in Ref. [51]. Section 8 summarizes the results obtained in Ref. [40] in relation with the study of the dissipativity of the Duhem model. Section 9 summarizes some results obtained in Ref. [64] in relation with the existence of a Duhem operator, its smoothness, and some generalizations of the model. Section 10 is a note that explores the minor loops of hysteresis systems with particular emphasis on the Duhem model. For ease of reference, some results on the existence and uniqueness of the solutions of differential equations are presented in Appendix 15.
To illustrate the results obtained in Sects. 4–10, and to analyze the relationships between these results, we use the scalar semilinear Duhem model as a case study. The corresponding mathematical analysis is stated in various lemmas and theorems provided in Section 11, whose proofs are given in 16–20. The relationships between the results obtained in Sects. 4–9 are commented upon in Section 12. These comments lead to the formulation of several open problems in Sect. 13 and a conjecture in Sect. 11.9.
3 Terminology and Notations
A real number x is said to be strictly positive when x>0
An ordered pair a, b is denoted (a, b) whilst the open interval {t∈R∣a<t<b}
The Lebesgue measure on R
W1,∞(R+,Rl)
L∞(R+,Rl)
C0(R+,Rl)
∀γ∈]0,∞[
limx↑a
Let U be a set and let T∈]0,∞[
4 A Summary of the Results Obtained in Ref. [43]
This section presents those results obtained in Ref. [43] that are relevant to the present paper. This is in particular the case of the concept of vibro-correctness which allows to extend the set of admissible inputs from continuously differentiable to continuous.
4.1 The Concept of Vibro-Correctness
Definition 1
In the following we analyze the consequences of vibro-correctness. Consider a sequence of inputs uk∈E(δ0,u∗)
Thus, the concept of vibro-correctness allows to extend the definition of the operator W
Another consequence of Property (ii) is the uniqueness of the solutions of (6)–(7). This means that it is not necessary to state explicitly in Property (i) that the differential equation (6)–(7) has a unique solution (this is what is done in Ref. [43]; see also [43, p. 104]).
Definition 2
[43, p. 98] If we consider only constant inputs u∗
4.2 Global Solutions of the Scalar Rate-Independent Duhem Model
4.3 Continuity of the Rate-Independent Duhem Model Seen as an Operator
For any given initial condition x0∈R
Theorem 2
[43, Theorem 29.1] The operatorZx0
sup{u∈S(t0,t2)∣‖u‖S≤a}‖Zx0(u)‖S<∞
5 A Summary of the Results Obtained in Ref. [54]
This section presents those results obtained in Ref. [54] that are relevant to the present paper. In particular, the authors of Ref. [54] propose a definition that decides whether a given generalized Duhem model is a hysteresis or not.
5.1 The Generalized Duhem Model
Assumption 1
For every (u,x0)∈W1,∞(R+,R)×Rn
From Assumption 1 we get y∈C0(R+,R)∩L∞(R+,R)
Define the operator Ho:W1,∞(R+,R)×Rn→C0(R+,R)∩L∞(R+,R)
5.2 Definition of Hysteresis According to Ref. [54]
We stress that Ref. [54] does not propose a definition of hysteresis in general. Instead, the authors of Ref. [54] propose a definition that decides whether a given generalized Duhem model is a hysteresis or not (this is Definition 4). We now present the different steps that are followed in Ref. [54] to come to Definition 4.
Definition 3
The nonempty set C⊂R2
- (i)
the function u is continuous on R+
R+ , - (ii)
the function u is continuously differentiable on ]0,α1[
]0,α1[ and on ]α1,T[]α1,T[ with ‖˙u‖<∞∥u˙∥<∞ , - (iii)
the function u is strictly increasing on ]0,α1[
]0,α1[ and is strictly decreasing on ]α1,T[]α1,T[ , - (iv)
we have u(0)=u(T)=umin
u(0)=u(T)=umin and u(α1)=umaxu(α1)=umax .
Assumption 2
Under Assumption 1, for every u∈Λ
Definition 4
- (i)
There exists a closed curve Cu⊂R2
Cu⊂R2 such that limγ→∞d2(Cu,Cu,γ)=0limγ→∞d2(Cu,Cu,γ)=0 . - (ii)
There exist a,b1,b2∈R
a,b1,b2∈R with b1≠b2b1≠b2 such that (a,b1)∈Cu(a,b1)∈Cu and (a,b2)∈Cu(a,b2)∈Cu .
Remark 1
Condition (i) in Definition 4 states that limγ→∞d2(Cu,Cu,γ)=0
Remark 2
Owing to Theorem 1, the generalized Duhem model (17)–(19) is not vibro-correct when the function g is not linear. This implies that it cannot be extended to continuous inputs by the use of the concept of vibro-correctness [43, p. 279]. If g is linear it is shown in [54, Proposition 3.2] that, for u∈Λ
5.3 Case Study
The semilinear Duhem model is used to illustrate Definition 4 and to analyze the relationship between Definition 4 and the concept of strong consistency presented in Sect. 6. To this end Section 11.5 provides an analytical study of the conditions under which the scalar semilinear Duhem model is a hysteresis according to Definition 4. This study is illustrated by numerical simulations in Sect. 11.6. Finally the relationship between Definition 4 and strong consistency is analyzed in Sect. 12.1.
6 A Summary of the Results Obtained in Ref. [35]
This section presents those results obtained in Ref. [35] that are relevant to the present paper. This is in particuler the case for the concepts of consistency and strong consistency.
6.1 The Normalized Input
Iu=[0,ρu,max]
Iu=[0,ρu,max] if ρu,max=ρu(t)ρu,max=ρu(t) for some t∈R+t∈R+ (in this case the interval IuIu is finite),Iu=[0,ρu,max[
Iu=[0,ρu,max[ if ρu,max>ρu(t)ρu,max>ρu(t) for all t∈R+t∈R+ (in this case the interval IuIu may be finite or infinite).
Lemma 1
[35] Letu∈W1,∞(R+,Rp)
μ({ϱ∈Iu∣˙ψu(ϱ) is not defined or |˙ψu(ϱ)|≠1})=0
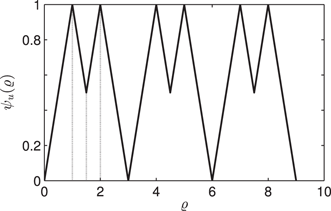
The function ψu
Lemma 1 shows that the input u has been “normalized” so that the resulting function ψu
For every γ∈]0,∞[
Lemma 2
[35] ∀γ∈]0,∞[,Iu∘sγ=Iu
6.2 Class of Operators
Let Ξ,U,Y
Assumption 3
[35] Let Ξ
6.3 The Normalized Output
Lemma 3
[35] LetΞ
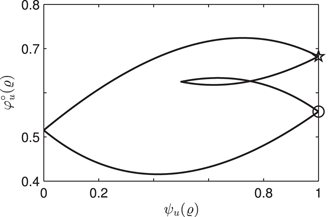
The function φu
Note that the correct notation for function φu
6.4 Definition of Consistency
Definition 5
[35] Let Ξ
Lemma 4
[35] LetΞ
The converse of Lemma 4 is not true in general [35, Example 2].
Definition 6
14 Let Ξ
Assumption 4
Let Ξ
The new element that Assumption 4 introduces is that the output H(u,x0)
Proposition 1
Under Assumption 4, let the operator H⋆:W1,∞(R+,Rp)×Ξ→L∞(R+,Rm)∩C0(R+,Rm)
Proof
Straightforward.
6.5 Definition of Strong Consistency
Observe that, in Definition 5 of consistency, the input u may be periodic or not. However, to characterize the hysteresis loop of the operator H
Lemma 5
[35] LetT∈]0,∞[
Definition 7
[35] Let Ξ
Definition 8
Note that the hysteresis loop Gu
Observe that some operators may be strongly consistent but do not describe a hysteresis, like any static nonlinearity y=f(u)
Definition 9
- (i)
The operator H
H is strongly consistent with respect to (u,x0)(u,x0) . - (ii)
μ({ϱ1∈Iu∣∃ϱ2∈Iu such that ψu(ϱ1)=ψu(ϱ2) and φ∘u(ϱ1)≠φ∘u(ϱ2)})≠0
μ({ϱ1∈Iu∣∃ϱ2∈Iu such that ψu(ϱ1)=ψu(ϱ2) and φ∘u(ϱ1)≠φ∘u(ϱ2)})≠0 .
6.6 Case Study
7 A Summary of the Results Obtained in Ref. [51]
This section presents those results obtained in Ref. [51] that are relevant to the present paper. In particular, Ref. [51] characterizes the function g that appears in Eq. (17).
Consider the generalized Duhem model (17)–(18) under Assumption 1. Let λ∈]0,∞[
Assumption 5
The limits limw↓0g(w)wλ
Assumption 5 implies that λ
Assumption 6
There exists a continuous function Q:R+×R+×R+→R+
Under Assumptions 1, 5, and 6 we have the following.
Lemma 6
- (i)
If λ∈]0,1[
λ∈]0,1[ then f(⋅,⋅)g(⋅)f(⋅,⋅)g(⋅) is identically zero. - (ii)
If λ∈]1,∞[
λ∈]1,∞[ then φ⋆uφ⋆u (see Sect. 6.4) is identically x0x0 . - (iii)If λ=1
λ=1 , let qu=φ⋆u∘ρuqu=φ⋆u∘ρu (see Sect. 6.1) thenqu(t)=x0+∫t0f(qu(τ),u(τ))ˆg(˙u(τ))dτ,∀t∈[0,∞[qu(t)=x0+∫t0f(qu(τ),u(τ))g^(u˙(τ))dτ,∀t∈[0,∞[ (32)ˆg(ϑ)={ϑlimw↓0g(w)wϑ≥0,|ϑ|limw↑0g(w)|w|ϑ<0.g^(ϑ)=⎧⎩⎨⎪⎪⎪⎪⎪⎪ϑlimw↓0g(w)w|ϑ|limw↑0g(w)|w|ϑ≥0,ϑ<0. (33)
Proof
(i) follows from Lemma 12 and Remark 14 in Ref. [51], whereas (ii) and (iii) are given in [51, Lemma 12].
Lemma 6 says that if λ≠1
8 A Summary of the Results Obtained in Ref. [40]
This section presents those results obtained in Ref. [40] that are relevant to the present paper. This is the case for the dissipativity of a special form of the Duhem model. The concept of dissipativity/passivity is treated in [42, chapter 6] as an abstracted form of energy dissipation which makes this concept relevant to the study of hysteresis.
8.1 The Scalar Rate-Independent Duhem Model
8.2 Definition of Dissipativity
Define the operator Φ:AC(R+,R)×R→AC(R+,R)
Definition 10
8.3 Sufficient Conditions for the Dissipativity of the Scalar Rate-Independent Duhem Model
Assumption 7
[40] The implicit function v↦{x1∈R∣F1(x1,v)=0}
Such a function fan
For every (x0,u0)∈R2
- (i)
ωΦ(Ω(x0,u0),x0,u0)=fan(Ω(x0,u0)),∀(x0,u0)∈R2
ωΦ(Ω(x0,u0),x0,u0)=fan(Ω(x0,u0)),∀(x0,u0)∈R2 , - (ii)
Ω(x0,u0)≥u0
Ω(x0,u0)≥u0 whenever x0≥fan(u0)x0≥fan(u0) , - (iii)
Ω(x0,u0)<u0
Ω(x0,u0)<u0 whenever x0<fan(u0)x0<fan(u0) , - (iv)
dΩ(x(t),u(t))dt
dΩ(x(t),u(t))dt exists for almost all t∈R+t∈R+ , and for all u∈AC(R+,R)u∈AC(R+,R) where x=Φ(u,x0)x=Φ(u,x0) .
Theorem 3
- (i)
There exists an intersecting functionΩ
Ω that corresponds to ωΦωΦ andfanfan , - (ii)
F1(x1,v)≥0
F1(x1,v)≥0 wheneverx1≤fan(v)x1≤fan(v) , andF1(x1,v)<0F1(x1,v)<0 otherwise.
A sufficient condition for the existence of an intersecting function is provided in the following lemma.
Lemma 7
- (i)
f1(x1,v)<dfan(v)dv−ϵ
f1(x1,v)<dfan(v)dv−ϵ whenever x1>fan(v)x1>fan(v) , and - (ii)
f2(x1,v)<dfan(v)dv−ϵ
f2(x1,v)<dfan(v)dv−ϵ whenever x1<fan(v)x1<fan(v) .
8.4 Extension of the Results Obtained in Ref. [40]
Similar results are given in Ref. [40] when the equation F1(x1,v)=0
8.5 Case Study
The scalar rate-independent semilinear Duhem model is used in Sect. 11.7 to illustrate the concept of dissipativity. To this end, the results of Ref. [40] are used to derive explicit conditions on the model parameters to ensure dissipativity. These conditions are illustrated by numerical simulations in Sect. 11.8. The relationship between dissipativity and orientation of the hysteresis loop is commented upon in Sect. 12.3.
9 A Summary of the Results Obtained in Ref. [64]
This section presents those results obtained in Ref. [64] that are relevant to the present paper. In particular, a local Lipschitz property of the Duhem model is provided.
Theorem 4
- (i)
For any u∈W1,1([0,T],R)
u∈W1,1([0,T],R) and any x0∈Rx0∈R there exists a unique x∈W1,1([0,T],R)x∈W1,1([0,T],R) such that Eqs. (43)–(45) hold. That is, we can define an operator M:W1,1([0,T],R)×R→W1,1([0,T],R)M:W1,1([0,T],R)×R→W1,1([0,T],R) by the relation M(u,x0)=xM(u,x0)=x . - (ii)
For any u∈C1([0,T],R)
u∈C1([0,T],R) we have x∈C1([0,T],R)x∈C1([0,T],R) . Moreover, for any x0∈Rx0∈R , the mapping M(⋅,x0)M(⋅,x0) is continuous in W1,1([0,T],R)W1,1([0,T],R) with respect to either the strong and the weak topology.
Proposition 2
[64, Proposition 1.3] Assume that ∀R>0,∃L(R)>0∣∀(xi,vi)∈R2(i=1,2)
Then, ∀x0∈R
It is shown in [64, Theorem 1.5] that the operator M
Section 12.2 provides comments on the relationship between Proposition 2 and the effect of noise on the hysteresis loop of the Duhem model.
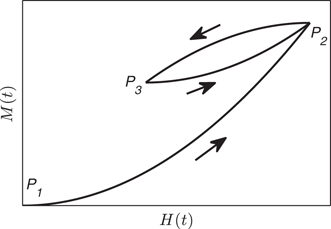
10 A Note on Minor Loops
The minor loops of the Duhem model have not been studied formally in the available literature. However, their behavior is important as evidenced by the large number of published works dedicated to their study both from an experimental point of view, and from a mathematical point a view for the Preisach model (see for example Ref. [49] and the references therein).
For this reason, we provide in this section the formal definition of a minor loop and analyze the behavior of the minor loops of the scalar semilinear Duhem model in Sect. 11.9. The material provided in this section may be used as a platform to attract mathematicians to the formal analysis of the minor loops of the Duhem model.
The path P1→P2
The loop formed by the path P2→P3→P2
In what follows we formalize mathematically the behavior observed in Fig. 2.
- (i)
the function u is continuous on R+
R+ , - (ii)
the function u is continuously differentiable on ]0,α1[
]0,α1[ , ]α1,α2[]α1,α2[ , ]α2,α3[]α2,α3[ , and ]α3,T[]α3,T[ with ‖˙u‖<∞∥u˙∥<∞ , - (iii)
the function u is strictly increasing on ]0,α1[
]0,α1[ , strictly decreasing on ]α1,α2[]α1,α2[ , strictly increasing on ]α2,α3[]α2,α3[ , and strictly decreasing on ]α3,T[]α3,T[ , - (iv)
we have u(0)=u(T)=umin,1
u(0)=u(T)=umin,1 , u(α1)=umax,1u(α1)=umax,1 , u(α2)=umin,2u(α2)=umin,2 , u(α3)=umax,2u(α3)=umax,2 .
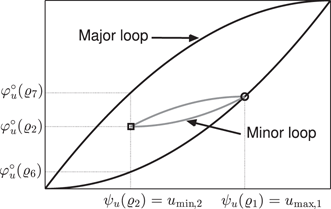
ψu(ϱ)
Assumption 8
∀(u,x0)∈Mumin,1,umin,2,umax,1,umax,2,α1,α2,α3,T×Ξ
Definition 11
- (i)
Vu∩Nu={(ψu(ϱ1),φ∘u(ϱ1))=(ψu(ϱ5),φ∘u(ϱ5))}.
Vu∩Nu={(ψu(ϱ1),φ∘u(ϱ1))=(ψu(ϱ5),φ∘u(ϱ5))}. - (ii)
φ∘u(ϱ6)<φ∘u(ϱ2)<φ∘u(ϱ7)
φ∘u(ϱ6)<φ∘u(ϱ2)<φ∘u(ϱ7) or φ∘u(ϱ7)<φ∘u(ϱ2)<φ∘u(ϱ6)φ∘u(ϱ7)<φ∘u(ϱ2)<φ∘u(ϱ6) .
Hysteresis loop φ∘u(ϱ)
The concepts introduced in this section are applied to the scalar semilinear Duhem model in Sect. 11.9.
11 Case Study: The Semilinear Duhem Model
In this section we use the semilinear Duhem model to illustrate the concepts presented in this paper, and to analyze the relationships between these concepts. Section 11.1 presents the model. In Sect. 11.2 we provide sufficient conditions for the consistency of the model. Section 11.3 focuses on the study of the strong consistency of the semilinear Duhem model. The results of Sects. 11.2 and 11.3 are illustrated by numerical simulations in Sect. 11.4. In Sect. 11.5 we specialize into the scalar version of the semilinear Duhem model. Section 11.5 provides the conditions under which the scalar semilinear Duhem model is a hysteresis according to Definition 4. The results of Sect. 11.5 are illustrated by numerical simuations in Sect. 11.6. The relationship between Definition 4 and strong consistency is commented upon in Sect. 12.1. Section 11.7 analyzes the dissipativity of the scalar rate-independent semilinear Duhem model. The results of Sect. 11.7 are illustrated by numerical simulations in Sect. 11.8. The relationship between dissipativity and orientation of the hysteresis loop is commented upon in Sect. 12.3. The minor loops of the scalar semilinear Duhem model are studied and commented upon in Sect. 11.9.
11.1 The Semilinear Duhem Model: Definition and Global Existence of Solutions
As noted in Ref. [54], the semilinear Duhem model is rate independent when g1(w)=max(0,w)
11.2 Consistency of the Semilinear Duhem Model
This section presents the results obtained in Ref. [35] in relation with the consistency of the semilinear Duhem model.
Theorem 5
[35] Consider the semilinear Duhem model (63)–(65). Assume that both matricesA1
In Eqs. (63)–(65) consider the operators H′s:L∞(R+,R)×W1,∞(R+,R)×Rn→W1,∞(R+,R)
Observe that the operators H′s
Consider the left-derivative operator Δ−
Theorem 6
11.3 Strong Consistency of the Semilinear Duhem Model
This section presents the results obtained in Ref. [35] in relation with the strong consistency of the semilinear Duhem model.
Theorem 7
Special cases22
Special case 2. We consider that u∈Λumin,umax,α1,T
Lemma 8
Proof
See Appendix 19.
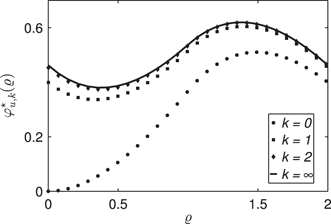
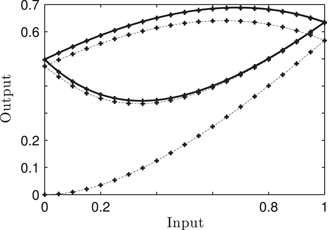
11.4 Illustration of the Consistency and Strong Consistency of the Scalar Semilinear Duhem Model
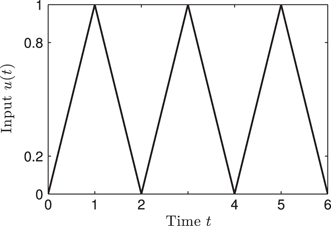
We consider the semilinear Duhem model with the following parameters: n=1,
u(t) versus t.
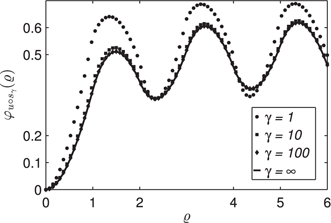
Dotted: φu∘sγ(ϱ)
Dotted: φ⋆u,k(ϱ)
φ∘u(ϱ)
11.5 Hysteresis Property -According to Definition 4- of the Scalar Semilinear Duhem Model
In this section we focus on the scalar version of the semilinear Duhem model (63)–(65), that is we consider that n=1
Our aim is to check whether the scalar semilinear Duhem model is a hysteresis according to Definition 4. To this end, we need to check whether Assumptions 1 and 2 hold as a prerequisite for Definition 4. Owing to Theorem 5 we can see that x∈W1,∞(R+,R)
Now, we have to check whether Assumption 2 is satisfied. To this end, let γ∈]0,∞[
When the semilinear Duhem model is rate independent, x0,γ
However, Ref. [54] provides no proof that Assumption 2 is satisfied for the rate-dependent semilinear Duhem model. Instead, another argument is used in the proof of [54, Proposition 5.1] to check whether the rate-dependent semilinear Duhem model is a hysteresis according to Definition 4 (or equivalently [54, Definition 2.2]). As shown in Section 12.1.3, that argument does not imply necessarily that Assumption 2 is satisfied.
In what follows we prove that Assumption 2 is satisfied for both the rate-independent and the rate-dependent scalar semilinear Duhem model.
Theorem 8
Consider the semilinear Duhem model (63)–(65) withn=1
Proof
See Appendix 17.
Theorem 8 shows that Assumption 2 is satisfied (see Remark 1). Our objective now is to prove that Conditions (i) and (ii) of Definition 4 are met. We start with Condition (i).
Theorem 9
limγ→∞d2(Cu,γ,Cu)=0
Proof
See Appendix 18.
Recall that the operator Ho
Lemma 9
Lemma 9 has not been derived in Ref. [54].
As a conclusion for the present section, when n=1
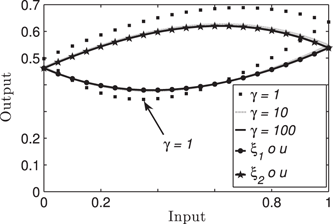
11.6 Illustration of the Hysteresis Property-According to Definition 4- of the Semilinear Duhem Model
Dotted: [Ho(u∘sγ,x0)](t)
The value x0,γ
In Fig. 10 observe that the point (u∘sγ(t),[Ho(u∘sγ,x0)](t))
Now we plot the closed curve Cu,γ
Cu,γ
11.7 Dissipativity of the Scalar Rate-Independent Semilinear Duhem Model
Lemma 10
Proof
See Appendix 20.
From Inequality (39) it follows that ς(x(t),u(t))−ς(x(0),u(0))≤∫t0˙x(τ)u(τ)dτ
Theorem 3 provides sufficient conditions for the function ς
Remark 3
All upward lines go up from left to right;
All downward lines go down from right to left.”
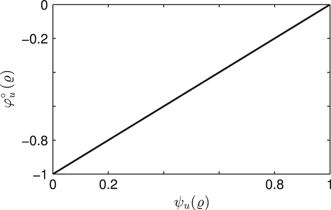
In Duhem’s notations, x is the input and X the output so that Condition (117), which is the same as dXdx>0
Remark 4
In Ref. [58] sufficient conditions are provided for the rate-independent semilinear Duhem model to have counterclockwise dynamics. However, unlike Ref. [40], these conditions depend on the explicit solution of the model, which may not be easy to translate into conditions on the model’s parameters.
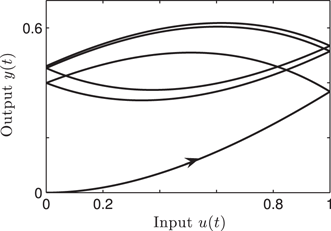
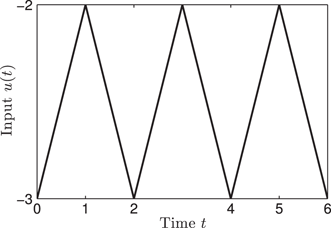
11.8 Illustration of the Dissipativity of the Scalar Rate-Independent Semilinear Duhem Model
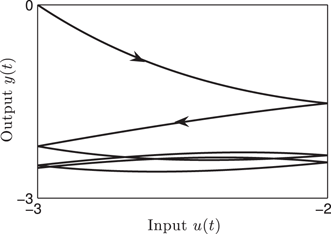
y(t) (=x(t)
Input u(t) versus time t.
y(t) versus u(t)
11.9 Minor Loops of the Scalar Semilinear Duhem Model
In this section we apply the concepts introduced in Sect. 10 to the scalar semilinear Duhem model.
Lemma 11
Consider the semilinear Duhem model (63)–(65) withn=1
Proof
See Appendix 21.
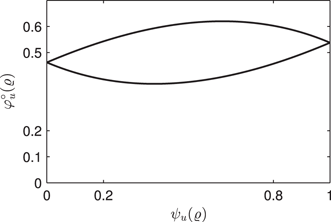
ψu(ϱ)
φ∘u(ϱ)
We now use the value E2=2
Lemma 11 says that the scalar semilinear Duhem model cannot represent the hysteresis behavior observed in magnetic hysteresis. Indeed, to produce minor loops that satisfy Assumption 8, the hysteresis loop of the model should be trivial.
This observation leads to the following conjecture.
Conjecture 1
Consider the generalized Duhem model (17)–(19). Assume that the corresponding operators Ho
If true, the conjecture would mean that the Duhem model -in its generalized form- is not able to describe the minor loops in magnetic hysteresis.
However, in several engineering problems, the Duhem model is not used to reproduce the behavior of minor loops in magnetic hysteresis. For example, in control problems, it is not necessary to have an accurate model that describes the controlled process with precision. Instead, an approximate model may be appropriate if it captures some essential features of the controlled plant, and at the same time, is simple enough to allow the design of a relatively simple controller (see for example Ref. [36]).
12 Relationships Between Concepts
In this section we explore the connections that exist between the concepts presented in this paper. We use the case study of the semilinear Duhem model to illustrate these connections and motivate the open problems proposed in Sect. 13.
12.1 Relationship Between Definition 4 and Strong Consistency
In this section we compare the definitions of hysteresis loop implied by Definition 4 and the concept of strong consistency.
12.1.1 Comments on Definition 4
Similarly it is not necessary to get the explicit expression of the closed curve Cu
Knowing the explicit expression of Cu,γ
Let us illustrate that statement. To prove that Condition (i) of Definition 4 holds for the scalar semilinear Duhem model we have demonstrated Equality (174). This equality is obtained thanks to the explicit expression (103) of the initial condition x0,γ
To sum up, the linearity with respect to the state in the differential equation that describes the scalar semilinear Duhem model, is crucial to prove that Condition (i) of Definition 4 holds. For a generalized Duhem model (17) that does not enjoy this linearity property it may not be easy to check analytically whether Condition (i) of Definition 4 holds.
12.1.2 Comments on Strong Consistency
To check whether a given generalized Duhem model is strongly consistent we have first to check whether it is consistent. The analysis of the consistency of the semilinear Duhem model is provided in Sect. 11.2, and it uses both the linearity with respect to the state, and the fact that the initial condition in Eq. (70) does not change with γ
Also checking the strong consistency of the semilinear Duhem model in Sect. 11.3 is made possible because it is not necessary to find the explicit expression of the initial state x∘u(0)
12.1.3 Relationship Between the Hysteresis Loop Derived from Definition 4 and the One Derived from Strong Consistency
The hysteresis loop derived from Definition 4 is the set Cu
Do we have Cu=Gu
For the scalar semilinear Duhem model the answer is positive. Indeed, the set Cu
However, for the generalized Duhem model, at the time of the submission of the present paper we do not know whether the sets Cu
Note that the authors of Ref. [54] assume tacitly that, for the semilinear Duhem model, we have Cu=Gu
For the Preisach model, defining the concept of a hysteresis loop is simple because the model does not have a transient response under the usual conditions. This means that the hysteresis loop is simply the graph output versus input. For the -possibly- rate-dependent generalized Duhem model, the output contains typically a transient term and a steady-state term. This is why there are two possibilities for defining a hysteresis loop: as the set Cu
The following comment sheds more light on the question.
Consider an operator H
- (i)
An operator H⋆
H⋆ that is rate independent with respect to linear time-scale changes, - (ii)
and an operator H†
H† such that the output H†(u∘sγ,x0)H†(u∘sγ,x0) vanishes when γ→∞γ→∞ (loosely speaking, the output vanishes when the frequency of the input goes to zero).
For all these reasons, we call Eqs. (28)–(29) the canonical decomposition of the operator H
This canonical decomposition was possible owing to the use of the concept of consistency.
12.2 Relationship Between the Lipschitz Property and the Effect of Perturbations
In this section we analyze the effect of a perturbation of the input and the initial condition on the hysteresis loop.
Consider a causal operator H:W1,∞(R+,Rp)×Ξ→L∞(R+,Rm)
Let the T–periodic input u∈W1,∞(R+,Rp)
Let ε∈W1,∞(R+,Rp)
Assumption 9
Iv=R+
Assumption 10
For any (w,y0)∈W1,∞(R+,Rp)×Ξ
This observation leads to formulating Open Problem 2 in Sect. 13.2.
We now consider the effect of perturbations on the hysteresis loop of the generalized Duhem model (17). Observe that, from Eq. (122) it comes that the quantity q(u,x0,ε,ϵ)
12.3 Relationship Between Dissipativity and Orientation of the Hysteresis Loop
For the scalar rate-independent Duhem model (34)–(36), dissipativity is the property of Definition 10. Dissipativity is studied in Ref. [40] mainly because of its interest in control. In this section, we focus on the relationship between dissipativity and the orientation of the hysteresis loop, as this orientation is easy to obtain experimentally.
At the time of the submission of this paper, we do not know whether a dissipative model (34)–(36) is strongly consistent. This observation leads to the formulation of Open Problem 3 in Sect. 13.3.
If the model (34)–(36) is dissipative and strongly consistent, then the hysteresis loop is oriented counterclockwise [1].
Theorem 3 provides sufficient conditions to ensure dissipativity. One of these conditions is f1≥0
The question of how to generalize Lemma 10 to encompass the model (34)–(36) leads to formulating Open Problem 4 in Sect. 13.4.
Note that there is no need to generalize Lemma 10 to encompass the generalized Duhem model (17) since the hysteresis loop is characterized by the rate-independent Duhem model (124)–(125).
13 Open Problems
13.1 Open Problem 1
The motivation for Open Problem 1 is provided in Sect. 12.1.3.
Consider that the generalized Duhem model (17)–(19) satisfies Assumption 1 so that we can define the operators Ho
- (i)
Find sufficient conditions that ensure Cu=Gu
Cu=Gu for all (u,x0)∈Λ×Rn(u,x0)∈Λ×Rn . - (ii)
Find a generalized Duhem model such that there exist an input u∈Λ
u∈Λ and an initial condition x0∈Rnx0∈Rn that satisfy Cu≠GuCu≠Gu .
13.2 Open Problem 2
The motivation for Open Problem 2 is provided in Sect. 12.2.
- (i)
Find sufficient conditions that provide an upper bound on ‖Hs(u,x0)−Hs(v,x′0)‖W1,∞([0,T],R)
∥Hs(u,x0)−Hs(v,x′0)∥W1,∞([0,T],R) for some finite real number T>0T>0 . Can we obtain an upper bound that is a continuous function of (‖u−v‖W1,∞([0,T],R),|x0−x′0|)(∥u−v∥W1,∞([0,T],R),|x0−x′0|) and that becomes the bound obtained in Proposition 2 when x0=x′0x0=x′0 ? - (ii)
Let T∈]0,∞[
T∈]0,∞[ and assume that u is T–periodic. Find an upper bound on q(u,x0,ε,ϵ)q(u,x0,ε,ϵ) as tight as possible. - (iii)
Find sufficient conditions so that if |x0−x′0|+‖u−v‖W1,∞([0,T],R)
|x0−x′0|+∥u−v∥W1,∞([0,T],R) is small then q(u,x0,ε,ϵ)q(u,x0,ε,ϵ) is small. - (iv)
13.3 Open Problem 3
The motivation for Open Problem 3 is provided in Sect. 12.3.
- (i)
Can we conclude that Hs
Hs is strongly consistent with respect to all periodic inputs u∈W1,∞(R+,R)u∈W1,∞(R+,R) and all initial states x0∈Rx0∈R ?
13.4 Open Problem 4
The motivation for Open Problem 4 is provided in Sect. 12.3.
- (i)Find a set S as large as possible of pairs (u,x0)∈W1,∞(R+,R)×R
(u,x0)∈W1,∞(R+,R)×R for which (i)–1 and (i)–2 hold.- (i)–1.
The operator Hs
Hs is strongly consistent with respect to all (u,x0)∈S(u,x0)∈S . - (i)–2.
The curve ϱ↦(ψu(ϱ),φ∘u(ϱ))
ϱ↦(ψu(ϱ),φ∘u(ϱ)) is counterclockwise for all (u,x0)∈S(u,x0)∈S .
- (i)–1.
- (ii)
14 Epilogue
More research is needed to better understand Duhem’s model seen as a class of differential equations, and also as a representation of hysteresis. In particular, it is important to get answers to the open problems -and to the conjecture- proposed in this paper.
There are no specified authors. The one-page preface written by M. V. cites the following people as co–authors or co–authors to be: M. Edouard Jordan, M. J. Hadamard, M. L. Marchis, M. H. Pélabon, M. Ed. Le Roy, and M. Darbon. However, the chapters bear the following names. The biography of P. Duhem is written by E. Jordan. The “Notice sur les titres et travaux scientifiques de Pierre Duhem” is the note Duhem wrote himself when he applied to the Académie des Sciences. The following chapter “La physique de P. Duhem” is written by Octave Manville. The chapter “L’œuvre de Pierre Duhem dans son aspect mathématique” is authored by J. Hadamard. Finally “L’histoire des sciences dans l’œuvre de P. Duhem” is written by A. Darbon.
For a detailed study of the life and work of Pierre-Maurice-Marie Duhem (9 June 1861–14 September 1916) see Refs. [39] or [67].
Ref. [48] cites a translation into German of the original memoir Ref. [16] which is written in French.
Quoting from Ref. [48, p. 96]: “the Madelung paper does not use a differential equation or integral operator. In fact, Madelung allows nonuniqueness of trajectories through a point…
The term “rate independence” is attributed to Truesdell and Noll (Section 99, Encyclopedia of Phyics, volume III/3, 1965) by Visintin [64, p. 13]. We read Section 99 of the 2004 edition [62] of the original treatise by Truesdell and Noll but found no clear evidence of the correctness of the attribution.
In this paper we avoid the words “positive”, “negative”, “increasing”, “decreasing” as they mean different things in different books.
If the functions hℓ
Ref. [54] considers that u is continuous and piecewise C1
The uniqueness of x0,u
In the proof of [54, Proposition 5.1] Oh and Bernstein use as input u∘sγ
To the best of our knowledge, proposing a formal definition of hysteresis based on the existence of a hysteresis loop was first done by Oh and Bernstein in Ref. [54] for the generalized Duhem model, and for inputs belonging to Λ
Indeed, if λ∈]0,1[
The condition that functions λ1,λ2
Since all the results of this section are proved for a finite time interval, Ref. [64] considers that the differential equation (43)–(44) holds almost everywhere on that finite time interval. We consider that the differential equation (43)–(44) holds almost everywhere on R+
If limw↓0ˉg1(w)=a1≠0
Funding
This study was funded by the Spanish Ministry of Economy, Industry and Competitiveness (Grant Number DPI2016-77407-P (AEI/FEDER, UE).
Compliance with Ethical Standards
Conflict of interest
The author declares that they have no conflict of interest.