A generic problem with purely metric formulations of MOND

• M.E Soussa ,
• R.P Woodard

• Department of Physics, University of Florida, Gainesville, FL 32611, USA

Received 27 September 2003, Accepted 24 October 2003, Available online 19 November 2003

Editor: M. Cvetič

http://dx.doi.org/10.1016/j.physletb.2003.10.090

---

PACS

• 04.50.+h;
• 11.10.Lm;
• 98.80.Cq

---

1. Introduction

A large spiral galaxy might contain a mass of M∼10¹¹M_⊙∼10⁴¹ kg in the form of stars and gas. Almost all of this mass lies inside a radius of R∼10 kpc∼10^20–21 m. With numbers on these scales it is easy to see that the gravitational acceleration ought to be Newtonian,

Hence neutral Hydrogen in a circular orbit of radius r>R should be observed to move more slowly as r increases, As is well known, it does not. In the scores of galaxies for which high quality rotation curves can be obtained [1], one actually finds that the asymptotic speed approaches a constant which is proportional to the fourth root of the total luminosity. This is known as the Tully–Fisher relation [2].

Dark matter is the conventional explanation for the observed failure of the Newtonian prediction (2). It was originally invoked to provide the mass necessary for Newtonian gravitation to bind galaxies to their host clusters [3] and [4]. To explain flat rotation curves it is supposed that galaxies are surrounded by halos of weakly-interacting, non-relativistic particles whose contribution to the total mass density falls off much more slowly than the mass density in stars and gas [5] and [6].

Dark matter has been impressively successful in reconciling the observed universe with general relativity and its Newtonian limit [6]. However, it is not without problems. First, there has been no direct detection of the particles which comprise it, except for neutrinos which can provide only a small fraction of the necessary mass and which are too light to cluster on galaxy scales. Second, what accounts for galactic rotation curves is an isothermal halo ρ_iso∼1/r² of dark matter. But numerical simulations of dark matter consistently produce the density profile of Navarro, Frenk and White [7], which falls like ρ_NFW∼1/r³ at large distances. Dark matter does not explain the Tully–Fisher relation. Nor can it elucidate the curious fact that the breakdown of Newtonian gravity, sourced by only the mass in stars and gas, seems to occur at the same characteristic acceleration (1) in cosmic structures of vastly different sizes. (But see [8].)

Milgrom has proposed that, instead of dark matter, galactic rotation curves signal a modification of gravity at very low accelerations [9]. If Newtonian theory predicts a gravitational acceleration , then the gravitational acceleration in Milgrom's theory (MOND) is,

The MOND interpolating function f(x) is assumed to vary smoothly between the stated limits. Many forms are consistent with the data. A typical example is In MOND a₀ has the status of a new universal constant. Its numerical value has been determined by fitting to nine well-measured galaxies [10],

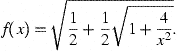
MOND was designed to explain the Tully–Fisher relation. In the MOND regime of a_N/a₀⪡1 one finds,

Making the natural assumption that the total luminosity L is proportional to the total mass one finds, v⁴_∞=a₀GM∝L, which is the Tully–Fisher relation  [2].

MOND not only reproduces the asymptotic rotation velocity v_∞, it also describes the inner portions of rotation curves. MOND fits have been worked up for on the order of 100 galaxies, using only the mass-to-luminosity ratios in stars and in gas as free parameters. The recent review paper by Sanders and McGaugh [1] summarizes the data and lists the primary sources. Except for a handful of galaxies that show evidence of recent disturbance, the fits are excellent. Further, the mass-to-luminosity ratios obtained from the fits are in rough agreement with evolution models [11]. It is especially significant that MOND even fits the rotation curves of low surface brightness galaxies [12] and [13], structures for which the MOND regime of a_N/a₀≲1 applies throughout and for which no detailed measurements had been made when the theory was proposed. Although some dark matter is needed to explain the temperature and density profiles of large galaxy clusters [14], it has been suggested that this might be provided by neutrinos without affecting the galaxy results [15].

The chief problem with MOND is that it does not provide a complete theory of gravitation the way that general relativity does. Bekenstein and Milgrom [16] have given a satisfactory field theory for the nonrelativistic potential whose negative gradient gives the gravitational acceleration, . If ρ_m is the mass density, the Lagrangian for φ is,

where the interpolating function associated with (4) would be . The existence of this Lagrangian is very important because it establishes that MOND conserves energy, momentum and angular momentum. However, this model provides no information about the other gravitational potentials, or about time evolution. One must therefore make essentially ad hoc assumptions to test what MOND says about lensing [17], or about cosmology [18].

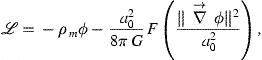
What is needed is a generally covariant formulation of MOND that includes at least the usual metric. A generally coordinate invariant, scalar-metric extension of the Bekenstein–Milgrom theory exists [16] but its prediction for the deflection of star light is identical to that of general relativity. Without dark matter, this gives far too little gravitational lensing from galaxies to be consistent with the data [19]. Scalar-metric models which reproduce MOND and may be consistent with extra-galactic lensing data can be constructed, but only at the price of allowing the scalar to carry negative energy [20] and [21].

Earlier this year we devised a generally covariant, purely metric model of MOND based on a nonlocal effective action [22]. Although we were able to reproduce the MOND force law, our model also failed to give the extra deflection of star light that would be provided in general relativity by dark matter. After studying the problem we have concluded that it is generic: any stable, generally covariant and metric-based theory of gravity that reproduces the MOND force law must suffer the same problem of too little lensing. The purpose of this Letter is to give a careful presentation of the argument. We do this in Section 2. Our model is presented in Section 3 to illustrate the problem. Section 4 identifies the five assumptions that lead to the generic problem. We also discuss the prospects for abandoning one of them.

2. The argument

We assume that the gravitational force is carried by the metric tensor g_μν(x) and that its source is the usual stress–energy tensor T_μν(x). This implies that the metric is determined by a set of ten field equations having the form,

We also assume that the theory of gravitation is generally covariant. This implies conservation, where the semi-colin denotes covariant differentiation. In general relativity would be the Einstein tensor, G_μν, but we make no assumptions about at this stage. In particular, we allow it to involve higher derivatives, and even to be a nonlocal functional of the metric.

Now recall that deviations between MOND and Newtonian gravitation become significant only for very small accelerations. These accelerations arise from derivatives of the metric. General coordinate invariance allows us to choose a coordinate system in which the metric agrees with the Minkowski metric η_μν at a single point. If its gradients are also small—which is the observed fact—then the metric can be made numerically quite close to η_μν over a large region. It therefore suffices to study Eq. (8) using weak field perturbation theory around flat space. That is, we write,

and we assume the numerical magnitude of the graviton field h_μν(x) is small in the MOND regime.

We wish to consider the weak field expansion of . In general relativity this begins at linear order, but that cannot be the case for any theory which reproduces the MOND force law. To see why, consider the gravitational response to a static distribution of total mass M, such as a low surface brightness galaxy, whose density is low enough that Eq. (8) is everywhere in the MOND regime. The MOND explanation (6) for the Tully–Fisher relation implies that at least one component of h_μν must scale like . (For spherical distributions it would be the rr component, but this does not matter.) How can (8) result in such a dependence? Since the right-hand side scales like GM, it follows that at least one tensor component of must go like h².

If we assume gravity is absolutely stable then all ten components of cannot begin at quadratic order in the weak field expansion. This is because the dynamical subset of the field equations follow from varying the gravitational Hamiltonian. If its variation were quadratic then the Hamiltonian would be cubic, and this is not consistent with stability. We therefore conclude that only a subset of the ten components of can go like h².

The desired subset must be distinguished in some generally covariant fashion. A symmetric, second rank tensor field contains two distinguished subsets: its divergence and its trace. The weak field expansion of the divergence does vanish a linearized order, but we see from conservation (9) that it vanishes to all orders. So the divergence cannot be responsible for the required h² term and we are left with the trace as the only remaining possibility,

Eq. (11) can explain the Tully–Fisher relation (6), but it means that MOND corrections to general relativity can be removed, in the weak field limit, by a local conformal rescaling of the metric,

To see why, recall that traceless metric field equations imply invariance under the transformation (12). (This has been known for decades. For a proof, see [23].) The full field equations are not traceless, so neither is the full theory conformally invariant. However, because the linearized field equations are traceless, the linearized theory must be conformally invariant. This means that the linearized field equations only determine the metric up to a conformal factor (and, of course, up to a linearized diffeomorphism). The conformal part of the metric is fixed by the order h² term in the trace of the field equations, and this is how one component of the weak field h_μν contrives to go like . But these MOND corrections to general relativity must be removable by a conformal rescaling (12), and possibly a simultaneous coordinate transformation.

This is a disaster for the phenomenology of gravitational lensing. To see why recall that, for a general metric g_μν, the Lagrangian of electromagnetism is,

where F_μν≡∂_μA_ν−∂_νA_μ. This Lagrangian is invariant under a conformal rescaling (12), which means that electromagnetism is unaware of MOND corrections to general relativity in the weak field limit. Hence the deflection of star light will be only that predicted by general relativity. Without dark matter this gives far too little lensing from galaxies [19]. That is the generic problem mentioned in the title of this Letter.

3. An example

Although the argument we have given is completely general, it is illuminating to see how the problem arises in a specific model. For this purpose we review the model whose failure motivated this study [22]. It is based on two nonlocal functionals of the metric. The first of these is known as the small potential,

We use a spacelike metric with R_μν≡Γ^ρ_νμ,ρ−Γ^ρ_ρμ,ν+Γ^ρ_ρσΓ^σ_νμ−Γ^ρ_νσΓ^σ_ρμ. The covariant d'Alembertian is inverted with retarded boundary conditions so that ϕ[g](x) depends only upon the metric and its derivatives evaluated on or inside the past light-cone of the point x^μ.

The second nonlocal functional in our construction is called, the large potential,

To reproduce the MOND force law it turns out that must obey [22],

For our model the functional is [22],

This form is manifestly covariant. It can be checked that it is also conserved. Although is nonlocal in our model, it is causal in the sense of depending only upon the fields on or inside the past light-cone of the point x^μ.

To prove asymptotic conformal invariance, note first that although the weak field expansion of the Ricci tensor R_μν involves arbitrary powers of the weak fields, it begins at linear order. This implies that the weak field expansion of the small potential (14) also begins at linear order. The same applies to the large potential (15) because it is proportional to the small potential in the MOND limit of ,

In taking the weak field limit of we can therefore neglect any products of R_μν, ϕ or Φ, such as G_μνΦ, ϕ^,ρΦ_,ρ and ϕ_,μϕ_,ν. We can also neglect . Hence the weak field limit of is contained in just four terms, Of course these terms involve many higher powers of h_μν, but they contain all the linear powers. And the terms we have kept are exactly traceless,

Note that tracelessness (and hence conformal invariance) is not a property of the full theory. In general the trace gives,

This goes like h² in the weak field expansion. It can be shown that the MOND terms in the force law derive entirely from the resulting quadratic equation [22], in accord with the general argument of Section 2.

4. Discussion

The point of making a no-go argument is to identify the assumptions which result in the negative conclusion. It can then be considered which, if any, of the assumptions might be discarded. For the argument given above we made the following assumptions:

•

the gravitational force is carried by the metric, and its source is the usual stress–energy tensor;

•

the theory of gravitation is generally covariant;

•

the MOND force law is realized in weak field perturbation theory;

•

the theory of gravitation is absolutely stable;

•

electromagnetism couples conformally to gravity.

It seems to us that the weakest assumption is absolute stability. This is what dictated that only a subset of the ten components of can be quadratic in the weak field expansion. If we abandon absolute stability it becomes possible that all ten components of are quadratic in the weak fields.

This may not be as bad as it sounds. It should be understood that any theory of MOND necessarily possesses two weak field regimes: the ultra-weak limit in which MOND applies, and a less-weak regime in which gravity is weak but MOND corrections to general relativity are negligible. It is the latter regime which describes the solar system and the interior of our galaxy, so gravity would still be stable in these settings.

The instability could only manifest in regions of very low gravitational acceleration. Even there it might be self-limiting because the creation of any significant density of decay products—whatever they are—would likely drive the theory back into the less-weak regime in which it is stable. So one might imagine a universe that very gradually decays, in the empty regions between galaxies, into long wave length particles whose density is diffused as the universe expands. If a₀ is really a constant this decay would only have started recently in cosmological history. And its further progress must be heavily suppressed by the intrinsic weakness of the gravitational interaction. We therefore conclude it is worth searching for a generally covariant, metric-based formulation of MOND in which all ten components of the field equations are quadratic in the weak field limit.

Even if no viable, generally covariant formulation of MOND can be constructed, this would in no way invalidate the impressive observational data that has been accumulated over many years [1]. The absence of an acceptable generalization of MOND would mean that this data is not explained by an alternate theory of gravitation, but we wish to stress that the data must still be explained. Either the low acceleration regime of gravity is ruled by some generalization of MOND or else isolated distributions of dark matter evolve towards some hitherto unrecognized attractor solution. Both alternatives are fascinating, and we feel the community is greatly indebted to those whose patient labors have drawn attention to the problem.

References

1. • [1]
   • R.H. Sanders, S.S. McGaugh

   • Annu. Rev. Astron. Astrophys., 40 (2002), p. 263 astro-ph/0204521

   • [SD-008]
2. • [2]
   • R.B. Tully, J.R. Fisher

   • Astron. Astrophys., 54 (1977), p. 661

   • [SD-008]
3. • [3]
   • F. Zwicky

   • Helv. Phys. Acta, 6 (1933), p. 110

   • [SD-008]
4. • [4]
   • S. Smith

   • Astrophys. J., 83 (1936), p. 23

   • [SD-008]
5. • [5]
   • G.R. Knapp, J. Kormendy

   • Dark Matter in the Universe

   • IAU Symposium No. 117 Reidel, Dordrecht (1987)

   • [SD-008]
6. • [6]
   • M.S. Turner

   • Phys. Rep., 333 (2000), p. 619

   • [SD-008]
7. • [7]
   • J.F. Navarro, C.S. Frenk, S.D.M. White

   • Astrophys. J., 490 (1997), p. 493

   • [SD-008]
8. • [8]
   • M. Kaplinghat, M. Turner

   • Astrophys. J., 569 (2002), p. L19 astro-ph/0107284

   • [SD-008]
9. • [9]
   • M. Milgrom

   • Astrophys. J., 270 (1983), p. 365

   • [SD-008]
10. • [10]
    • K.G. Begeman, A.H. Broeils, R.H. Sanders

    • Mon. Not. R. Astron. Soc., 240 (1991), p. 523

    • [SD-008]
11. • [11]
    • E.F. Bell, R.S. de Jong

    • Astrophys. J., 550 (2001), p. 212 astro-ph/0011493

    • [SD-008]
12. • [12]
    • S.S. McGaugh, W.J.G. de Blok

    • Astrophys. J., 449 (1998), p. 66 astro-ph/9801102

    • [SD-008]
13. • [13]
    • W.J.G. de Blok, S.S. McGaugh

    • Astrophys. J., 508 (1998), p. 132 astro-ph/9805120

    • [SD-008]
14. • [14]
    • A. Aguirre, J. Schaye, E. Quataert

    • Astrophys. J., 561 (2001), p. 550 astro-ph/0105184

    • [SD-008]
15. • [15]
    • R.H. Sanders

    • Mon. Not. R. Astron. Soc., 342 (2003), p. 901 astro-ph/0212293

    • [SD-008]
16. • [16]
    • J.D. Bekenstein, M. Milgrom

    • Astrophys. J., 286 (1984), p. 7

    • [SD-008]
17. • [17]
    • D.J. Mortlock, E.L. Turner

    • Mon. Not. R. Astron. Soc., 372 (2001), p. 557 astro-ph/0106100

    • [SD-008]
18. • [18]
    • R.H. Sanders

    • Astrophys. J., 560 (2001), p. 1 astro-ph/0011439

    • [SD-008]
19. • [19]
    • D.J. Mortlock, E.L. Turner

    • Mon. Not. R. Astron. Soc., 372 (2001), p. 552 astro-ph/0106099

    • [SD-008]
20. • [20]
    • J.D. Bekenstein

    • Phys. Rev. D, 48 (1993), p. 3641 gr-qc/9211017

    • [SD-008]
21. • [21]
    • J.D. Bekenstein, R.H. Sanders

    • Astrophys. J., 429 (1994), p. 480 astro-ph/9311062

    • [SD-008]
22. • [22]
    • M.E. Soussa, R.P. Woodard

    • Class. Quantum Grav., 20 (2003), p. 2737 astro-ph/0302030

    • [SD-008]
23. • [23]
    • N.C. Tsamis, R.P. Woodard

    • Ann. Phys., 168 (1986), p. 457

    • [SD-008]

Copyright © 2003 Elsevier B.V. All rights reserved.