Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics

doi:10.3390/e16084521

Open Access This article is

freely available
re-usable

Entropy 2014, 16(8), 4521-4565; doi:10.3390/e16084521

Article

Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics

Frédéric Barbaresco

Thales Air Systems, Advanced Radar Concepts Business Unit, Voie Pierre-Gilles de Gennes, Limours F-91470, France; E-Mail: frederic.barbaresco@thalesgroup.com; Tel.: +33-(0)630071419

Received: 30 March 2014; in revised form: 11 June 2014 / Accepted: 23 June 2014 /
Published: 12 August 2014

Abstract

: The François Massieu 1869 idea to derive some mechanical and thermal properties of physical systems from “Characteristic Functions”, was developed by Gibbs and Duhem in thermodynamics with the concept of potentials, and introduced by Poincaré in probability. This paper deals with generalization of this Characteristic Function concept by Jean-Louis Koszul in Mathematics and by Jean-Marie Souriau in Statistical Physics. The Koszul-Vinberg Characteristic Function (KVCF) on convex cones will be presented as cornerstone of “Information Geometry” theory, defining Koszul Entropy as Legendre transform of minus the logarithm of KVCF, and Fisher Information Metrics as hessian of these dual functions, invariant by their automorphisms. In parallel, Souriau has extended the Characteristic Function in Statistical Physics looking for other kinds of invariances through co-adjoint action of a group on its momentum space, defining physical observables like energy, heat and momentum as pure geometrical objects. In covariant Souriau model, Gibbs equilibriums states are indexed by a geometric parameter, the Geometric (Planck) Temperature, with values in the Lie algebra of the dynamical Galileo/Poincaré groups, interpreted as a space-time vector, giving to the metric tensor a null Lie derivative. Fisher Information metric appears as the opposite of the derivative of Mean “Moment map” by geometric temperature, equivalent to a Geometric Capacity or Specific Heat. We will synthetize the analogies between both Koszul and Souriau models, and will reduce their definitions to the exclusive Cartan “Inner Product”. Interpreting Legendre transform as Fourier transform in (Min,+) algebra, we conclude with a definition of Entropy given by a relation mixing Fourier/Laplace transforms: Entropy = (minus) Fourier₍_Min_,₊₎ o Log o Laplace₍₊_,_X₎.PACS Codes: 02 (Mathematical methods in physics), 05 (Statistical physics, thermodynamics, and nonlinear dynamical systems)

Keywords:

Koszul-Vinberg characteristic function; Koszul forms; Koszul entropy; temperature vector; covariant thermodynamics; Souriau-Gibbs equilibrium state

1. Introduction

The Koszul-Vinberg Characteristic Function (KVCF) is a dense knot in important mathematical fields such as Hessian Geometry, Kählerian Geometry and Affine Differential Geometry. As essence of Information Geometry, this paper develops KVCF as a transverse concept in Thermodynamics, in Statistical Physics and in Probability. From general KVCF definition, the paper introduces Koszul Entropy as the Legendre transform of minus the logarithm of KVCF, and compares both functions by analogy with the Dual Massieu-Duhem potentials in thermodynamics. This paper will also explore close inter-relations between these domains through geometric tools developed by Jean-Louis Koszul and Jean-Marie Souriau. The cornerstone of “Information Geometry” Theory will appear to be based on the fundamental property that derivatives of the Koszul-Vinberg Characteristic Function Logarithm $(KVCFL) log ψ_{Ω} (x) = log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ$ , defined on convex dual cone of Ω, are invariant by the automorphisms of Ω, and that its hessian defines a non-arbitrary Riemannian metric.

In thermodynamics, François Massieu [1–3] was the first to introduce the concept of characteristic function φ. This characteristic function or thermodynamic potential is able to provide all the body properties from their derivatives. In thermodynamics, Entropy S is one of the Massieu-Duhem potentials [4–8], derived from the Legendre-Moreau transform of the characteristic function logarithm $φ : S = φ - β \cdot \frac{\partial φ}{\partial β}$ with $β = \frac{1}{k T}$ being the thermodynamic temperature. The most popular notion of “characteristic function” was introduced in a second step by Henri Poincaré in his lecture on probability [9,10], using the property that all moments of statistical laws could be deduced from its derivatives. Paul Levy then made systematic use of this concept in his 1925 book. We assume that Poincaré was influenced by his school fellow at Ecole des Mines de Paris, François Massieu, and his work on thermodynamic potentials (generalized by Pierre Duhem in an Energetic Theory). This assertion is corroborated by the observation that Poincaré added in his lecture on thermodynamics in the 2nd edition [9,10] in 1892, a chapter on the “Massieu characteristic function” with many developments and applications, before developing the concept in Probability [9,10], see Figure 1.

In Thermodynamics, Statistical Physics and Probability, we can observe that the “characteristic function” and its derivatives capture all information of system or physical model and random variable. Furthermore, the general notion of Entropy could be naturally defined by the Legendre Transform of minus the Koszul characteristic function logarithm. In the general case, Legendre transform of minus the logarithm of the KVCF will be designated in the following as “Koszul Entropy”.

This general notion of “characteristic function” has been generalized by the French physicist Jean-Marie Souriau. In 1970, Souriau, that had followed the Elie Cartan Lecture at ENS Ulm in 1946 (one year after his aggregation), introduced the concept of co-adjoint action of a group on its momentum space (or “moment map”: mapping induced by symplectic manifold symmetries), based on the orbit method works, that allows to define physical observables like energy, heat and momentum as pure geometrical objects (the moment map takes its values in a space attached to the group of symmetries in the dual space of its Lie algebra). The moment map is a constant of the motion and is associated to symplectic cohomology (assignment of algebraic invariants to a topological space that arises from the algebraic dualization of the homology construction). For Souriau, equilibrium states are indexed by a geometric parameter β with values in the Lie algebra of the dynamical group (Galileo or Poincaré group). The Souriau approach generalizes the Gibbs equilibrium states, β playing the role of temperature. The invariance with respect to the group, and the fact that the entropy S is a convex function of β, imposes very strict conditions, that allow Souriau to interpret β as a space-time vector (the vector-valued temperature of Planck), giving to the metric tensor a null Lie derivative. For Souriau, all the details of classical mechanics appear as geometric necessities (e.g., mass is the measure of the symplectic cohomology of the action of a Galileo group). We will synthetize the analogies between the Koszul and Souriau models in tables (the Information Geometry case being a particular case of Koszul Hessian geometry).

The Koszul-Vinberg characteristic function is a dense knot in mathematics and could be introduced in the framework of different geometries: Hessian Geometry (Jean-Louis Koszul’s work), Homogeneous convex cones geometry (Ernest Vinberg’s work [11]), Homogeneous Symmetric Bounded Domains Geometry [12,13] (Elie Cartan [14] and Carl Ludwig Siegel’s works [15,16]), Symplectic Geometry [17,18] (Thomas von Friedrich [19] & Jean-Marie Souriau’s work), Affine Geometry (Takeshi Sasaki and Eugenio Calabi’s works) and Information Geometry (Calyampudi Rao and Nikolai Chentsov’ works). Through Legendre duality, Contact Geometry (Vladimir Arnold’s work) is considered as the odd-dimensional twin of symplectic geometry and could be used to understand Legendre mapping in Information Geometry. Fisher metrics of Information Geometry could be introduced as hessian metrics from minus Koszul-Vinberg characteristic function logarithm or from Koszul Entropy (Legendre transform of minus Koszul-Vinberg characteristic function logarithm). In a more general context, we can consider Information Geometry in the framework of “Geometric Science of Information”, a new “corpus” that also covers probability in metric space (Maurice Fréchet’s work), probability/geometry on structures (Yann Ollivier and Misha Gromov’s works [20–23]) and probability on Riemannian manifold (Michel Emery and Marc Arnaudon’s works). This link between “Information Theory” and “Geometry” is also deeply developed and influenced by fundamental works of Yann Ollivier [24,25] (initially described in his HDR report “Randomness and Curvature” in 2009 and more recent papers on IGO flow).

2. Legendre Duality and Projective Duality

In following chapters, we will see that the minus Logarithm of the Characteristic Function and Entropy will be related by the Legendre transform, that can be considered in the context of projective duality. Duality is an old and very fruitful idea in mathematics that has been constantly generalized [26–38]. A duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation and sometimes with fixed points.

The simplest duality is linear duality in the plane with points and lines (two different points can be joined by a unique line. Two different lines meet in one point unless they are parallel). By adding some points at infinity (to avoid particular case of parallel lines) then we obtain the projective plane in which the duality is given symmetrical relationship between points and lines, and led to the classical principle of projective duality, where the dual theorem is also a theorem.

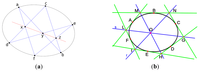
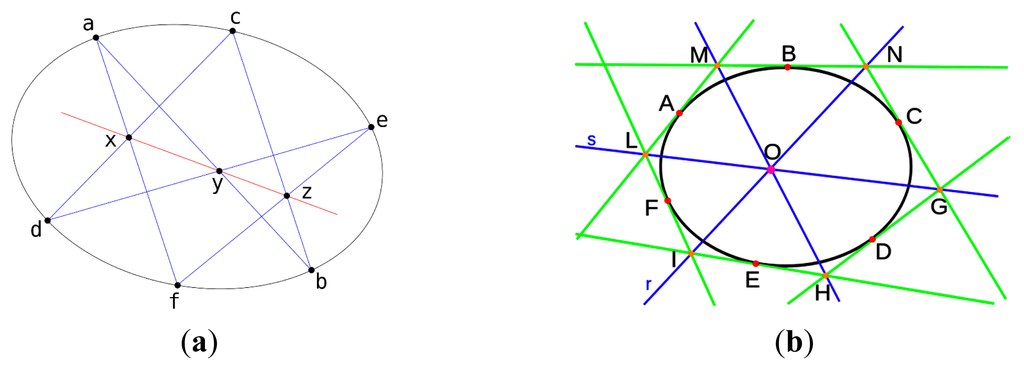
Most Famous example is given by Pascal’s theorem (the Hexagrammum Mysticum Theorem) stating that:

If the vertices of a simple hexagon are points of a point conic, then its diagonal points are collinear: If an arbitrary six points are chosen on a conic (i.e., ellipse, parabola or hyperbola) and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon (extended if necessary) meet in three points which lie on a straight line, called the Pascal line of the hexagon.

The dual of Pascal’s Theorem is known as Brianchon’s Theorem, as illustrated in Figure 2:

If the sides of a simple hexagon are lines of a line conic, then the diagonal lines are concurrent.

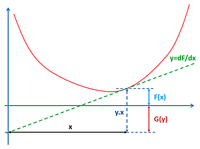
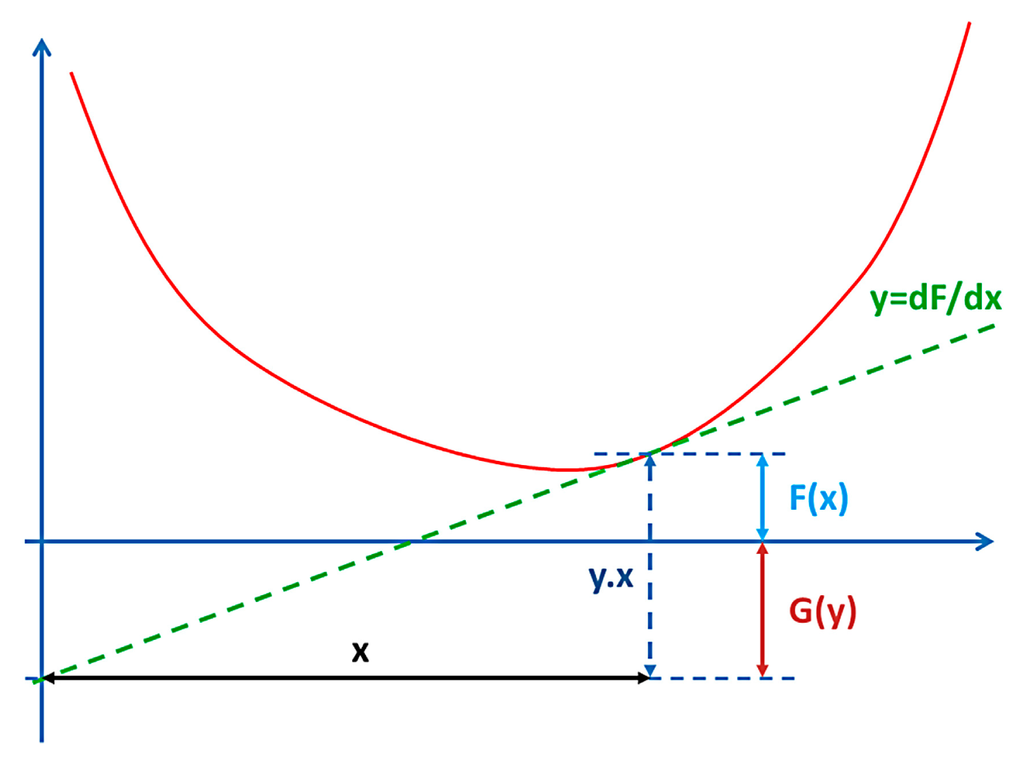
The Legendre(-Moreau) transform [39,40] is an operation from convex functions on a vector space to functions on the dual space. The Legendre transform is related to projective duality and tangential coordinates in algebraic geometry, and to the construction of dual Banach spaces in analysis. Classical Legendre transform in Euclidean space is given by fixing a scalar product 〈.,.〉 on Rⁿ. For a function F:Rⁿ → R∪{±∞}, let:

(1)

G (y) = L F (y) = \underset{x}{S u p} {〈 y, x 〉 - F (x)}

The Legendre transform is illustrated in Figure 3.

This is an involution on the class of convex lower semi-continuous functions on Rⁿ. There are two dual possibilities to describe a function. We can either use a function, or we may regard the curve as the envelope of its tangent planes. We give in Appendix A1 the historical context of Legendre Transform introduction on a Minimal Surface problem considered initially by Gaspard Monge.

The Legendre Transform is very important in Information Geometry [39], which uses mutually dual (conjugate) affine connections, dual potentials in dual coordinates systems and dual metrics that are studied in the framework of Hessian or affine differential geometry.

To illustrate the role of Legendre transform in Information Geometry, we provide a canonical example, with the relations for the Multivariate Normal Gaussian Law N(m,R):

- Dual Coordinates systems:
(2) ${\begin{array}{l} \tilde{Θ} = (θ, Θ) = (R^{- 1} m, {(2 R)}^{- 1}) \\ \tilde{H} = (η, H) = (m, - R + m m^{T}) \end{array}$
- Dual potential functions:
(3) ${\begin{array}{l} \tilde{Ψ} (\tilde{Θ}) = 2^{- 1} T r (Θ^{- 1} θ θ^{T}) - 2^{- 1} log (det Θ) + 2^{- 1} n log (2 π e) \\ \tilde{Φ} (\tilde{H}) = - 2^{- 1} log (1 + η^{T} H^{- 1} η) - 2^{- 1} log (det (- H)) - 2^{- 1} n log (2 π e) \end{array}$

related by Legendre transform:

(4)

\tilde{Φ} (\tilde{H}) = 〈 \tilde{Θ}, \tilde{H} 〉 - \tilde{Ψ} (\tilde{Θ}) with 〈 \tilde{Θ}, \tilde{H} 〉 = T r (θ η^{T} + Θ H^{T})

where dual coordinate systems are given by derivatives of dual potential functions:

(5)

{\begin{array}{l} \frac{\partial \tilde{Ψ}}{\partial θ} = η \\ \frac{\partial \tilde{Ψ}}{\partial Θ} = H \end{array} a n d {\begin{array}{l} \frac{\partial \tilde{Φ}}{\partial η} = θ \\ \frac{\partial \tilde{Φ}}{\partial H} = Θ \end{array}

with Φ̃(H̃) = E[log p] being the Entropy.

In the theory of Information Geometry introduced by Rao and Chentsov, a Riemannian manifold is then defined by a metric tensor given by hessian of these dual potential functions:

(6)

g_{i j} = \frac{\partial^{2} \tilde{Ψ}}{\partial {\tilde{Θ}}_{i} \partial {\tilde{Θ}}_{j}} and g_{i j}^{*} = \frac{\partial^{2} \tilde{Φ}}{\partial {\tilde{H}}_{i} \partial {\tilde{H}}_{j}}

In this paper, we will develop the concept of “Hessian Manifolds” theory that was initially studied by Koszul in a more general framework. In the next section, we will expose the theory of the Koszul-Vinberg characteristic function on convex sharp cones that will be presented as a general framework of Information Geometry.

3. Koszul Characteristic Function/Entropy by Legendre Duality

We define the Koszul-Vinberg Hessian metric on a convex sharp cone, and observe that the Fisher information metric of Information Geometry coincides with the canonical Koszul Hessian metric (given by Koszul forms) [41–47]. We also observe, by Legendre duality (Legendre transform of minus Koszul characteristic function logarithm), that we are able to introduce a Koszul Entropy, that plays the role of the generalized Shannon Entropy.

3.1. Koszul-Vinberg Characteristic Function and Metric for Convex Sharp Cone

Jean-Louis Koszul [41,42,47] and Ernest B. Vinberg [48,49] have introduced an affinely invariant hessian metric on a sharp convex cone Ω^* through its characteristic function ψ. In the following, Ω^* is a sharp open convex cone in a vector space E of finite dimension on R (a convex cone is sharp if it does not contain any full straight line). In dual space E^* of E, Ω^* is the set of linear strictly positive forms on Ω̄−{0}. Ω^* is the dual cone of Ω and is a sharp open convex cone. If ξ ∈ Ω^*, then the intersection Ω∩{x∈E/〈x,ξ〉 = 1} is bounded. G = Aut(Ω) is the group of linear transform of E that preserves Ω. G = Aut(Ω) operates on Ω^* by ∀g ∈ G = Aut(Ω), ∀ξ ∈ E^* then g̃.ξ = ξ ○ g⁻¹.

Koszul-Vinberg Characteristic Function Definition

Let dξ be the Lebesgue measure on E^*, the following integral:

(7)

ψ_{Ω} (x) = \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \forall x \in Ω

with Ω^* the dual cone is an analytic function on Ω, with ψ_Ω(x) ∈ ]0, +∞[, called the Koszul-Vinberg characteristic function of cone Ω.

The Koszul-Vinberg Characteristic Function has the following properties:

The Bergman kernel of Ω + iRⁿ⁺¹ is written as K_Ω(Re(z)) up to a constant where K_Ω is defined by the integral:
(8) $K_{Ω} (x) = \int_{Ω^{*}} e^{- 〈 ξ, x 〉} ψ_{Ω^{*}} {(ξ)}^{- 1} d ξ$
ψ_Ω is analytic function defined on the interior of Ω and ψ_Ω(x) → + ∞ as x → ∂Ω

If g ∈ Aut(Ω) then ψ_Ω (gx) = |det g|⁻¹ ψ_Ω (x) and since tI ∈ G = Aut(Ω) for any t > 0, we have

(9)

ψ_{Ω} (t x) = ψ_{Ω} (x) / t^{n}

ψ_Ω is logarithmically strictly convex, and φ_Ω (x) = log(ψ_Ω (x)) is strictly convex.

From the KVCF, could be introduced two forms defined by Koszul:

Koszul 1-form α

The differential 1-form

(10)

α = d φ_{Ω} = d log ψ_{Ω} = d ψ_{Ω} / ψ_{Ω}

is invariant by all automorphisms G = Aut(Ω) of Ω. If and u∈E then

(11)

〈 α_{x}, u 〉 = - \int_{Ω^{*}} 〈 ξ, u 〉 . e^{- 〈 ξ, x 〉} d ξ a n d α_{x} \in - Ω^{*}

and:

Koszul 2-form β

The symmetric differential 2-form:

(12)

β = D α = d^{2} log ψ_{Ω}

is a positive definite symmetric bilinear form on invariant under G = Aut(Ω). Dα > 0

This positivity is given by Schwarz inequality and:

(13)

d^{2} log ψ_{Ω} (u, v) = \int_{Ω^{*}} 〈 ξ, u 〉 〈 ξ, v 〉 e^{- 〈 ξ, u 〉} d ξ

We can then introduce the Koszul metric based on previous definitions:

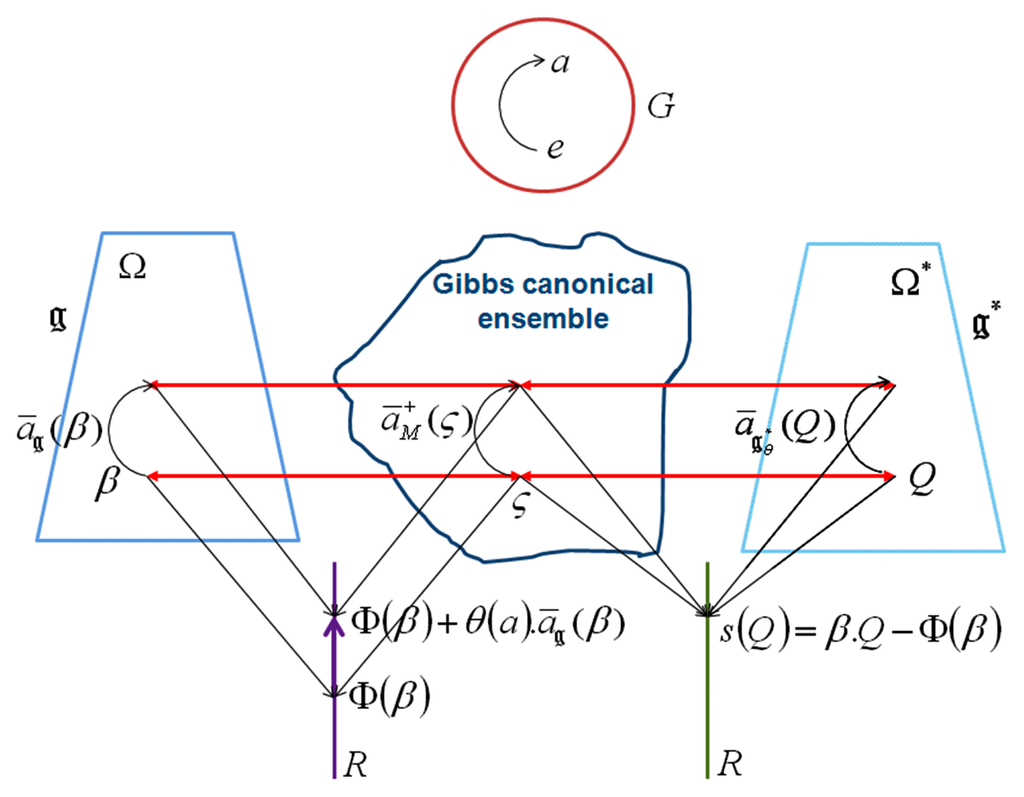
Koszul Metric

Dα defines a Riemanian structure invariant by Aut(Ω), and then the Riemanian metric is given by g = d² logψ_Ω

(14)

\begin{array}{l} (d^{2} log ψ (x)) (u) = \frac{1}{ψ {(u)}^{2}} [\int_{Ω^{*}} F {(ξ)}^{2} d ξ . \int_{Ω^{*}} G {(ξ)}^{2} d ξ - {(\int_{Ω^{*}} F (ξ) . G (ξ) d ξ)}^{2}] > 0 \\ with F (ξ) = e^{- \frac{1}{2} 〈 x, ξ 〉} and G (ξ) = e^{- \frac{1}{2} 〈 x, ξ 〉} 〈 u, ξ 〉 \end{array}

This result is obtained using Schwarz inequality, $d log ψ = \frac{d ψ}{ψ}$ and $d^{2} log ψ = \frac{d^{2} ψ}{ψ} - {(\frac{d ψ}{ψ})}^{2}$ where $(d ψ (x)) (u) = - \int_{Ω^{*}} e^{- 〈 x, ξ 〉} 〈 u, ξ 〉 d ξ$ and $(d^{2} ψ (x)) (u) = - \int_{Ω^{*}} e^{- 〈 x, ξ 〉} {〈 u, ξ 〉}^{2} d ξ$ A diffeomorphism is used to define dual coordinate:

(15)

x^{*} = - α_{x} = - d log ψ_{Ω} (x)

with $〈 d f (x), u 〉 = D_{u} f (x) = {\frac{d}{d t} |}_{t = 0} f (x + t u)$ . When the cone Ω is symmetric, the map x ↦ x^* = −α_x is a bijection and an isometry with one unique fixed point (the manifold is a Riemannian Symmetric Space given by this isometry):

(16)

{(x^{*})}^{*} = x, 〈 x, x^{*} 〉 = n and ψ_{Ω} (x) ψ_{Ω^{*}} (x^{*}) = c s t e

x^* is characterized by x^* = arg min {ψ(y)/y ∈ Ω^*, 〈x, y〉 = n} and x^* is the center of gravity of the cross section {y ∈ Ω^*,〈x, y〉 = n} of Ω^* :

(17)

x^{*} = \int_{Ω^{*}} ξ . e^{- 〈 ξ, x 〉} d ξ / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ and 〈 - x^{*}, h 〉 = d_{h} log ψ_{Ω} (x) = - \int_{Ω^{*}} 〈 ξ, h 〉 e^{- 〈 ξ, x 〉} d ξ / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ

If we set Φ(x) = −logψ_Ω(x), Misha Gromov [20,21] has observed that x^* = dΦ(x) is an injection where the closure of the image equals the convex hull of the support and the volume of this hull is the the n-dimensional volume defined by the integral of the determinant of the hessian of this function Φ(x), where the map $Φ \mapsto M (Φ) = \int_{Ω} det (H e s s (Φ (x))) . d x$ obeys non-trivial convexity relation given by the Brunn-Minkowsky inequality [M(Φ₁ + Φ₂)]^1/ⁿ ≥ [M(Φ₁)]^1/ⁿ + [M(Φ₂)]^1/ⁿ.

3.2. Koszul Entropy and Its Barycenter

From this last equation, we can deduce the “Koszul Entropy” defined as the Legendre Transform of Φ(x) minus logarithm of Koszul-Vinberg characteristic function:

(18)

\begin{matrix} Φ^{*} (x^{*}) = 〈 x, x^{*} 〉 - Φ (x) with x^{*} = D_{x} Φ and x = D_{x^{*}} Φ^{*} \\ where Φ (x) = - log ψ_{Ω} (x) \end{matrix}

(19)

Φ^{*} (x^{*}) = 〈 {(D_{x} Φ)}^{- 1} (x^{*}), x^{*} 〉 - Φ [{(D_{x} Φ)}^{- 1} (x^{*})] \forall x^{*} \in {D_{x} Φ (x) / x \in Ω}

By the definition of the Koszul-Vinberg Characteristic function, and by using −〈ξ,x〉 = log e^−〈^ξ^,^x^〉. we can write:

(20)

- 〈 x^{*}, x 〉 = \int_{Ω^{*}} log e^{- 〈 ξ, x 〉} . e^{- 〈 ξ, x 〉} d ξ / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ

and:

(21)

\begin{array}{l} Φ^{*} (x^{*}) = 〈 x, x^{*} 〉 - Φ (x) = - \int_{Ω^{*}} log e^{- 〈 ξ, x 〉} . e^{- 〈 ξ, x 〉} d ξ / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ + log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \\ Φ^{*} (x^{*}) = [(\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ) .log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ - \int_{Ω^{*}} log e^{- 〈 ξ, x 〉} . e^{- 〈 ξ, x 〉} d ξ] / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \\ Φ^{*} (x^{*}) = [log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ - \int_{Ω^{*}} log e^{- 〈 ξ, x 〉} . \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} d ξ] \\ Φ^{*} (x^{*}) = [log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ . (\int_{Ω^{*}} \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} d ξ) - \int_{Ω^{*}} log e^{- 〈 ξ, x 〉} . \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} d ξ] with \int_{Ω^{*}} \frac{e^{- (ξ, x)}}{\int_{Ω^{*}} e^{- (ξ, x)} d ξ} d ξ = 1 \\ Φ^{*} (x^{*}) = [- \int_{Ω^{*}} \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} . log (\frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ}) d ξ] \end{array}

In this last equation, $p_{x} (ξ) = e^{- 〈 ξ, x 〉} / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ$ appears as a density, and the Legendre transform Φ^* () looks like the classical Shannon Entropy, named in the following Koszul Entropy:

(22)

Φ^{*} = - \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ

with:

(23)

p_{x} (ξ) = e^{- 〈 ξ, x 〉} / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} = e^{- 〈 x, ξ 〉 + Φ (x)} and x^{*} = \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ

We will call $p_{x} (ξ) = \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ}$ the Koszul Density, with the property that:

(24)

log p_{x} (ξ) = - 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = - 〈 x, ξ 〉 + Φ (x)

and:

(25)

E_{ξ} [- log p_{x} (ξ)] = 〈 x, x^{*} 〉 - Φ (x)

We can observe that:

(26)

\begin{array}{l} Φ (x) = - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = - log \int_{Ω^{*}} e^{- [Φ^{*} (ξ) + Φ (x)]} d ξ = Φ (x) - log \int_{Ω^{*}} e^{- Φ^{*} (ξ)} d ξ \\ \Rightarrow \int_{Ω^{*}} e^{- Φ^{*} (ξ)} d ξ = 1 \end{array}

But the development is not achieved and we have to make appear x^* in Φ^* (x^*). For this objective, we have to write:

(27)

\begin{array}{l} log p_{x} (ξ) = log e^{- 〈 x, ξ 〉 + Φ (x)} = log e^{- Φ^{*} (ξ)} = - Φ^{*} (ξ) \\ \Rightarrow Φ^{*} = - \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ = \int_{Ω^{*}} Φ^{*} (ξ) p_{x} (ξ) d ξ = Φ^{*} (x^{*}) \end{array}

The last equality is true if and only if we have the following relation:

(28)

\int_{Ω^{*}} Φ^{*} (ξ) p_{x} (ξ) d ξ = Φ^{*} (\int_{Ω^{*}} ξ . p_{x} (ξ) d ξ) as x^{*} = \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ

This condition could be written more synthetically [50,51]:

(29)

E [Φ^{*} (ξ)] = Φ^{*} (E [ξ]), ξ \in Ω^{*}

The meaning of this relation is that “the Barycenter of Koszul Entropy is the Koszul Entropy of Barycenter”.

This condition is achieved for x^* = D_xΦ taking into account Legendre Transform property:

(30)

\begin{array}{l} Legendre Transform : Φ^{*} (x^{*}) = \underset{x}{S u p} [〈 x, x^{*} 〉 - Φ (x)] \\ \Rightarrow {\begin{array}{l} Φ^{*} (x^{*}) \geq 〈 x, x^{*} 〉 - Φ (x) \\ Φ^{*} (x^{*}) \geq \int_{Ω^{*}} Φ^{*} (ξ) p_{x} (ξ) d ξ \end{array} \Rightarrow {\begin{array}{l} Φ^{*} (x^{*}) \geq E [Φ^{*} (ξ)] \\ equality for x^{*} = \frac{d Φ}{d x} \end{array} \end{array}

3.3. Relation of Koszul Density with the Maximum Entropy Principle

We will observe in this section that Koszul density is a solution of the Maximum Entropy. Classically, the density given by the Maximum Entropy Principle [52–58] is given by:

(31)

\underset{p_{x} (.)}{M a x} [- \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ] such {\begin{array}{l} \int_{Ω^{*}} p_{x} (ξ) d ξ = 1 \\ \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ = x^{*} \end{array}

If we take $q_{x} (ξ) = e^{- 〈 ξ, x 〉} / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ}$ such that:

(32)

{\begin{array}{l} \int_{Ω^{*}} q_{x} (ξ) . d ξ = \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = 1 \\ log q_{x} (ξ) = log e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} = - 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 x, ξ 〉} d ξ \end{array}

Then by using the fact that log x ≥ (1−x⁻¹) with equality if and only if x = 1, we find the following:

(33)

- \int_{Ω^{*}} p_{x} (ξ) log \frac{p_{x} (ξ)}{q_{x} (ξ)} d ξ \leq - \int_{Ω^{*}} p_{x} (ξ) (1 - \frac{q_{x} (ξ)}{p_{x} (ξ)}) d ξ

We can then observe that:

(34)

\int_{Ω^{*}} p_{x} (ξ) (1 - \frac{q_{x} (ξ)}{p_{x} (ξ)}) d ξ = \int_{Ω^{*}} p_{x} (ξ) d ξ - \int_{Ω^{*}} q_{x} (ξ) d ξ = 0

because $\int_{Ω^{*}} p_{x} (ξ) d ξ = \int_{Ω^{*}} q_{x} (ξ) d ξ = 1$

We can then deduce that:

(35)

- \int_{Ω^{*}} p_{x} (ξ) log \frac{p_{x} (ξ)}{q_{x} (ξ)} d ξ \leq 0 \Rightarrow - \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ \leq - \int_{Ω^{*}} p_{x} (ξ) log q_{x} (ξ) d ξ

If we develop the last inequality, using expression of q_x (ξ):

(36)

- \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ \leq - \int_{Ω^{*}} p_{x} (ξ) [- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 x, ξ 〉} d ξ] d ξ

(37)

- \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ \leq 〈 x, \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ 〉 + log \int_{Ω^{*}} e^{- 〈 x, ξ 〉} d ξ

If we take $x^{*} = \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ$ and $Φ (x) = - log \int_{Ω^{*}} e^{- 〈 x, ξ 〉} d ξ$ , then we deduce that the Koszul density $q_{x} (ξ) = e^{- 〈 ξ, x 〉} / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉 d ξ}}$ is the Maximum Entropy solution constrained by $\int_{Ω^{*}} p_{x} (ξ) d ξ = 1$ and $\int_{Ω^{*}} ξ . p_{x} (ξ) d ξ = x^{*}$ :

(38)

- \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ \leq 〈 x, x^{*} 〉 - Φ (x)

(39)

- \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ \leq Φ^{*} (x^{*})

We have then observed that Koszul Entropy provides density of Maximum Entropy:

(40)

p_{\bar{ξ}} (ξ) = \frac{e^{- 〈 ξ, Φ^{- 1} (\bar{ξ}) 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, Θ^{- 1} (\bar{ξ}) 〉} d ξ} with x = Θ^{- 1} (\bar{ξ}) and \bar{ξ} = Θ (x) = \frac{d Φ (x)}{d x}

where:

(41)

\bar{ξ} = \int_{Ω^{*}} ξ . p_{\bar{ξ}} (ξ) d ξ and Φ (x) = - log \int_{Ω^{*}} e^{- 〈 x, ξ 〉} d ξ

We can then deduce the Maximum Entropy solution without solving the classical variational problem with Lagrangian hyperparameters, but only by inversing function $\bar{ξ} = Θ (x) = \frac{d Φ (x)}{d x}$ . This remark was made by Jean-Souriau in the paper [59]. If we take vector with tensor components $ξ = (\begin{matrix} z \\ z \otimes z \end{matrix})$ , components of ξ̄ will provide moments of 1st and 2nd order of the density of probability p_ξ̄(ξ), that is defined by Gaussian law. In this particular case, we can write:

(42)

〈 ξ, x 〉 = a^{T} z + \frac{1}{2} z^{T} H z

with a ∈ Rⁿ and H ∈ Sym (n). By the change of variables given by z′ = H^1/2z + H^−1/2a, we can then compute the logarithm of the Koszul characteristic function:

(43)

Φ (x) = - \frac{1}{2} [a^{T} H^{- 1} a + log det [H^{- 1}] + n log (2 π)]

We can prove that the 1st moment is equal to −H⁻¹a and that components of variance tensor are equal to elements of matrix H⁻¹, that induces the second moment. The Koszul Entropy, defined as the Legendre transform of the Koszul characteristic function, is then given by:

(44)

Φ^{*} (\bar{ξ}) = = \frac{1}{2} [log det [H^{- 1}] + n log (2 π . e)]

3.4. Crouzeix Relation on Hessian of Dual Potentials and Its Consequences

In previous sections, we have used the duality between dual potential functions that is recovered by this relation:

(45)

Φ^{*} (x^{*}) + Φ (x) = 〈 x, x^{*} 〉 with x^{*} = \frac{d Φ}{d x} and x = \frac{d Φ^{*}}{{d x}^{*}} where Φ (x) = - log ψ_{Ω} (x)

If we develop relations, we can deduce that the hessian of one potential function is the inverse of the hessian of the dual potential function, then the Information Geometry metric could be given in two systems of dual coordinates:

(46)

\begin{array}{l} {\begin{array}{l} \frac{d Φ}{d x} = x^{*} \\ \frac{d Φ^{*}}{{d x}^{*}} = x \end{array} \Rightarrow {\begin{array}{l} \frac{d^{2} Φ}{{d x}^{2}} = \frac{{d x}^{*}}{d x} \\ \frac{d^{2} Φ^{*}}{{d x}^{* 2}} = \frac{d x}{{d x}^{*}} \end{array} \Rightarrow \frac{d^{2} Φ}{{d x}^{2}} . \frac{d^{2} Φ^{*}}{{d x}^{* 2}} = 1 \Rightarrow \frac{d^{2} Φ}{{d x}^{2}} = {[\frac{d^{2} Φ^{*}}{{d x}^{* 2}}]}^{- 1} \\ \Rightarrow d s^{2} = - \frac{d^{2} Φ}{{d x}^{2}} {d x}^{2} = - {[\frac{d^{2} Φ^{*}}{{d x}^{* 2}}]}^{- 1} . {[\frac{d^{2} Φ^{*}}{{d x}^{* 2}} . {d x}^{*}]}^{2} = - \frac{d^{2} Φ^{*}}{{d x}^{* 2}} . {d x}^{* 2} \end{array}

Gromov [22] observed that the hessian of the entropy Φ^* on the space of probability measure is positive definite by the Shannon inequality and defines a (non-complete) Riemannian metric, and that this metric is called the Fisher-Rao-Kramer, Antonelli-Strobeck, Svirezhev-Shahshahani, Karquist metric.

The relation $\frac{d^{2} Φ}{{d x}^{2}} = {[\frac{d^{2} Φ^{*}}{{d x}^{* 2}}]}^{- 1}$ has been established first by Crouzeix in 1977 in a short communication [60] for convex smooth functions and their Legendre transforms. This result has been extended for non-smooth function by Seeger [61] and Hiriart-Urruty [62], using a polarity relationship between the second-order sub-differentials. This relation was mentioned in texts of calculus of variations and theory of elastic materials (with work potentials) [62].

This last relation has also been used in the framework of the Monge-Ampere measure associated to a convex function, to prove equality with Lebesgue measure λ:

(47)

\begin{array}{l} m_{Φ} (Λ) = \int_{Λ} ϕ (x) d x = λ ({\nabla φ (x) / x \in Λ}) \\ \forall Λ \in B_{Ω} (Borel set in Ω) and ϕ (x) = det [\nabla^{2} Φ (x)] \end{array}

That is proved using the Crouzeix relation ∇²Φ(x) = ∇²Φ(∇Φ^*(y)) = [∇²Φ^*(y)]⁻¹:

(48)

\begin{array}{l} m_{Φ} (Λ) = \int_{Λ} ϕ (x) d x = \int_{Λ} det [\nabla^{2} Φ (x)] . d x \\ m_{Φ} (Λ) = \int_{{(\nabla Φ^{*})}^{- 1} (A)} det [\nabla^{2} Φ (\nabla Φ^{*} (y))] . det [\nabla^{2} Φ^{*} (y)] d y = \int_{\nabla Φ (Λ)} 1. d y = λ ({\nabla φ (x) / x \in Λ}) \end{array}

3.5. Fisher Information Geometry Metric as a Particular Case of Koszul Metric

To make the link with the classical Fisher metric given by Fisher Information matrix I (x) in Information Geometry, we can observe that the second derivative of log p_x (ξ) is given by:

(49)

\begin{array}{l} p_{x} (ξ) = e^{- 〈 ξ, x 〉} / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} \Rightarrow log p_{x} (ξ) = - 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \\ with Φ (x) = - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = - log ψ_{Ω} (x) \end{array}

(50)

\frac{\partial^{2} log p_{x} (ξ)}{\partial x^{2}} = \frac{\partial^{2} Φ (x)}{\partial x^{2}}

(51)

\Rightarrow I (x) = - E_{ξ} [\frac{\partial^{2} log p_{x} (ξ)}{\partial x^{2}}] = - \frac{\partial^{2} Φ (x)}{\partial x^{2}} = \frac{\partial^{2} log ψ_{Ω} (x)}{\partial x^{2}}

We could then deduce the close interrelation between Fisher metric and hessian of minus Koszul-Vinberg characteristic logarithm, that are totally equivalent. Information Geometry then appears as a particular case of Koszul Hessian Geometry.

We can also observed that the Fisher metric or hessian of KVCF logarithm is related to the variance of ξ:

(52)

log Ψ_{Ω} (x) = log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \Rightarrow \frac{\partial log Ψ_{Ω} (x)}{\partial x} = - \frac{1}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} \int_{Ω^{*}} ξ . e^{- 〈 ξ, x 〉} d ξ

(53)

\frac{\partial^{2} log Ψ_{Ω} (x)}{\partial x^{2}} = - \frac{1}{{(\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ)}^{2}} [- \int_{Ω^{*}} ξ^{2} . e^{- 〈 ξ, x 〉} d ξ . \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ + {(\int_{Ω^{*}} ξ . e^{- 〈 ξ, x 〉} d ξ)}^{2}]

(54)

\frac{\partial^{2} log Ψ_{Ω} (x)}{\partial x^{2}} = \int_{Ω^{*}} ξ^{2} . \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} d ξ - {(\int_{Ω^{*}} ξ . \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} d ξ)}^{2} = \int_{Ω^{*}} ξ^{2} . p_{x} (ξ) d ξ - {(\int_{Ω^{*}} ξ . p_{x} (ξ) d ξ)}^{2}

(55)

I (x) = - E_{ξ} [\frac{\partial^{2} log p_{x} (ξ)}{\partial x^{2}}] = \frac{\partial^{2} log ψ_{Ω} (x)}{\partial x^{2}} = E_{ξ} [ξ^{2}] - E_{ξ} {[ξ]}^{2} = V a r (ξ)

The Inverse of the Fisher/Information Matrix I(x) defines the lower bound of statistical estimators. Classically, this Lower bound is called Cramer-Rao Bound because it was described in the Rao’s paper of 1945 [63]. Historically, this bound has been published first by Maurice Fréchet in 1939 in his winter “Mathematical Statistics” Lecture at the Institut Henri Poincaré during winter 1939–1940. Maurice Fréchet has published these elements in a paper as early as 1943 [64]. We can read at the bottom of the first page of his paper [64]:

“Le contenu de ce mémoire a formé une partie de notre cours de statistique mathématique a l’Institut Henri Poincaré pendant l’hiver 1939–1940. Il constitue l’un des chapitres du deuxième cahier (en préparation) de nos «Leçons de Statistique Mathématique», dont le premier cahier, «Introduction: Exposé préliminaire de Calcul des Probabilités” (119 pages in-quarto, dactylographiées) vient de paraitre au «Centre de Documentation Universitaire, Tournois et Constans. Paris».”
[The contents of this report formed a part of our lecture of mathematical statistics at the Henri Poincaré institute during winter 1939–1940. It constitutes one of the chapters of the second exercise book (in preparation) of our “Lessons of Mathematical Statistics”, the first exercise book of which, “Introduction: preliminary Presentation of Probability theory” (119 pages quarto, typed) has just been published in the “Centre de Documentation Universitaire, Tournois et Constans. Paris”.]

3.6. Extended Results by Koszul, Vey and Sasaki

Koszul [41,65] and Vey [66,67] have developed extended results with the following theorem for connected hessian manifolds:

Koszul-Vey Theorem: Let M be a connected hessian manifold with hessian metric g. Suppose that M admits a closed 1-form α such that Dα = g and there exists a group G of affine automorphisms of M preserving α:

If M/G is quasi-compact, then the universal covering manifold of M is affinely isomorphic to a convex domain Ω of an affine space not containing any full straight line.
If M/G is compact, then Ω is a sharp convex cone.

On this basis, Koszul has given a Lie Group construction of a homogeneous cone that has been developed and applied in Information Geometry by Shima [68,69] and Boyom [70] in the framework of Hessian Geometry.

After the pioneering work of Koszul, Sasaki has developed the study of hessian manifolds in Affine Geometry [71,72]. He has denoted by S_c the level surface of ψ_Ω : S_c = {ψ_Ω(x) = c} which is a non-compact sub-manifold in Ω, and by ω_c the induced metric of d ² logψ_Ω on S_c, then assuming that the cone Ω is homogeneous under G(Ω), he proved that S_c is a homogeneous hyperbolic affine hypersphere and every such hyperspheres can be obtained in this way. Sasaki also remarks that ω_c is identified with the affine metric and S_c is a global Riemannian symmetric space when Ω is a self-dual cone. He concludes that, let Ω be a regular convex cone and let g = d² logψ_Ω be the canonical Hessian metric, then each level surface of the characteristic function ψ_Ω is a minimal surface of the Riemannian manifold (Ω,g).

3.7. Geodesics Equation for the Koszul Hessian Metric

The last contribution has been given by Rothaus [73] who studied the construction of geodesics for this hessian metric geometry, using the following property:

(56)

Γ_{j k}^{i} = \frac{1}{2} g^{i l} (\frac{\partial g_{l j}}{\partial x_{k}} + \frac{\partial g_{l k}}{\partial x_{j}} - \frac{\partial g_{j k}}{\partial x_{l}}) = \frac{1}{2} g^{i l} \frac{\partial^{3} log ψ_{Ω} (x)}{\partial x_{j} \partial x_{k} \partial x_{l}} with g_{i j} = \frac{\partial^{2} log ψ_{Ω} (x)}{\partial x_{i} \partial x_{j}}

or expressed also according the Christoffel symbol of the first kind:

(57)

Γ_{i j k} = \frac{1}{2} (\frac{\partial g_{j k}}{\partial x_{i}} + \frac{\partial g_{k i}}{\partial x_{j}} - \frac{\partial g_{i j}}{\partial x_{k}}) = \frac{1}{2} \frac{\partial^{3} log ψ_{Ω} (x)}{\partial x_{j} \partial x_{k} \partial x_{l}}

Then geodesic is given by:

(58)

\frac{d^{2} x_{k}}{d s^{2}} + Γ_{i j}^{k} \frac{d x_{i}}{d s} \frac{d x_{j}}{d s} = g_{k l} \frac{d^{2} x_{k}}{d s^{2}} + Γ_{i j k} \frac{d x_{i}}{d s} \frac{d x_{j}}{d s} = 0

that could be developed with previous relation:

(59)

\frac{d^{2} x_{k}}{{d s}^{2}} \frac{\partial^{2} log ψ_{Ω}}{\partial x_{k} \partial x_{l}} + \frac{1}{2} \frac{d x_{i}}{d s} \frac{d x_{j}}{d s} \frac{\partial^{3} log ψ_{Ω}}{\partial x_{l} \partial x_{i} \partial x_{j}} = 0

We can then observe that:

(60)

\frac{d^{2}}{{d s}^{2}} [\frac{\partial log ψ_{Ω}}{\partial x_{l}}] = \frac{d x_{i}}{d s} \frac{d x_{j}}{d s} \frac{\partial^{3} log ψ_{Ω}}{\partial x_{i} \partial x_{j} \partial x_{l}} + \frac{d^{2} x_{k}}{{d s}^{2}} \frac{\partial^{2} log ψ_{Ω}}{\partial x_{k} \partial x_{l}}

The geodesic equation can then be rewritten:

(61)

\frac{d^{2} x_{k}}{{d s}^{2}} \frac{\partial^{2} log ψ_{Ω}}{\partial x_{k} \partial x_{l}} + \frac{d^{2}}{{d s}^{2}} [\frac{\partial log ψ_{Ω}}{\partial x_{l}}] = 0

That we can put in vector form using notations x^* = −d logψ_Ω and Fisher matrix I(x) = d² logψ_Ω:

(62)

I (x) \frac{d^{2} x}{{d s}^{2}} - \frac{d^{2} x^{*}}{{d s}^{2}} = 0 or I (x) = {[\frac{d^{2} x}{{d s}^{2}}]}^{- 1} \frac{d^{2} x^{*}}{{d s}^{2}}

3.8. Koszul Metric for Siegel Homogeneous Domains

Koszul [42] has developed his previously described theory for Homogenous Siegel Domains SD. He has proved that there is a subgroup G in the group of the complex affine automorphisms of these domains (Iwasawa subgroup), such that G acts on SD simply transitively. The Lie algebra g of G has a structure that is an algebraic translation of the Kähler structure of SD. There is an integrable almost complex structure J on, g and there exists η ∈ g^* such that 〈X, Y〉_η = 〈[JX,Y],η〉, defines a J-invariant positive definite inner product on g. Koszul has proposed as admissible form η ∈ g^*, the form ξ:

(63)

Ψ (X) = 〈 X, ξ 〉 = T r [a d (J X) - J . a d (X)] \forall X \in g

Koszul has proved that 〈X,Y〉_ξ coincides, up to a positive number multiple with the real part of the Hermitian inner product obtained by the Bergman metric of SD by identifying g with the tangent space of SD. The First Koszul form is then given by:

(64)

α = - \frac{1}{4} d Ψ (X)

We can illustrate this new Koszul expression for Poincaré’s Upper Half Plane V = {z = x + iy/y>0} (most simple symmetric homogeneous bounded domain).

Define vector fields $X = y \frac{d}{d x}$ and $Y = y \frac{d}{d y}$ , and J an almost complex structure on V defined by JX = Y

As:

(65)

[X, Y] = - Y and a d (Y) . Z = [Y, Z] then {\begin{array}{l} T r [a d (J X) - J a d (X)] = 2 \\ T r [a d (J Y) - J a d (Y)] = 0 \end{array}

The Koszul 1-form and then the Koszul/Poincaré metric is given by:

(66)

Ψ (X) = 2 \frac{d x}{y} \Rightarrow α = - \frac{1}{4} d Ψ = - \frac{1}{2} \frac{d x \land d y}{y^{2}} \Rightarrow {d s}^{2} = \frac{{d x}^{2} + {d y}^{2}}{2 y^{2}}

This could be also applied for Siegel’s Upper Half Space V = {Z = X + iY/X,Y ∈ Sym(p), Y > 0} (more natural extension of Poincaré Upper-half plane, and general notion of symmetric bounded homogeneous domains studied by Elie Cartan and Carl-Ludwig Siegel):

(67)

{\begin{array}{l} S Z = (A Z + B) D^{- 1} \\ A^{T} D = I, B^{T} D = D^{T} B \end{array} with S = (\begin{matrix} A & B \\ 0 & D \end{matrix}) and J = (\begin{matrix} 0 & I \\ - I & 0 \end{matrix})

(68)

Ψ (d X + i d Y) = \frac{3 p + 1}{2} T r (Y^{- 1} d X) \Rightarrow {\begin{array}{l} α = - \frac{1}{4} d Ψ = \frac{3 p + 1}{8} T r (Y^{- 1} d Z \land Y^{- 1} d \bar{Z}) \\ {d s}^{2} = \frac{(3 p + 1)}{8} T r (Y^{- 1} d Z Y^{- 1} d \bar{Z}) \end{array}

To recover the metric of the space of Symmetric Positive Definite (HPD) matrices, we take Z = iR (with X = 0), and obtain the metric ds² = Tr[(R⁻¹dR)]². In the context of Information Geometry, this metric is the metric for multivariate Gaussian law of covariance matrix R and zero mean. For more development and application for Radar signal processing, we give reference to author papers [74–77].

4. Souriau Geometric Temperature and Covariant Definition of Thermodynamic Equilibriums

Souriau, a student of Elie Cartan [78] at ENS Ulm in 1946, has given in [59,79–87] a covariant definition of thermodynamic equilibriums and has formulated statistical mechanics [88–90] and thermodynamics in the framework of Symplectic Geometry [59] by use of symplectic moments and distribution-tensor concepts, giving a geometric status for temperature, heat and entropy. This work has been extended by Vallée and de Saxcé [91–94], Iglésias [95,96] and Dubois [97]. Other recent works address equilibrium states on manifolds of negative curvature and could be analyzed in the framework of Information Geometry [98–103].

Other directions related to polarized surface have been developed by Donaldson, Guillemin and Abreu, in which invariant Kähler metrics correspond to convex functions on the moment polytope of a toric variety [104–108] based on precursor work of Atiyah and Bott [109] on moment map and its convexity by Bruguières [110], Condevaux [111], Delzant [112], Guillemin and Sternberg [113] and Kirwan [114]. More recently, Mikhail Kapranov has also given a thermodynamical interpretation of the moment map for toric varieties [115]. Readers may consult the tutorial paper of Biquard [116].

The first general definition of the “moment map” (constant of the motion for dynamical systems) was introduced by Souriau during 1970s, with geometric generalization of such earlier notions as the Hamiltonian and the invariant theorem of Noether describing the connection between symmetries and invariants (it is the moment map for a one-dimensional Lie group of symmetries). In symplectic geometry the analog of Noether’s theorem is the statement that the moment map of a Hamiltonian action which preserves a given time evolution is itself conserved by this time evolution. The conservation of the moment of a Hamilotnian action was called by Souriau the “Symplectic or Geometric Noether theorem” (considering phases space as symplectic manifold, cotangent fiber of configuration space with canonical symplectic form, if Hamiltonian has Lie algebra, moment map is constant along system integral curves. Noether theorem is obtained by considering independently each component of moment map).

In previous approach based on Koszul’s work, we have defined two convex functions Φ(x) and Φ^*(x^*) with dual system of coordinates x and x^* on dual cones Ω and Ω^*:

(69)

Φ (x) = - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \forall x \in Ω and Φ^{*} (x^{*}) = 〈 x, x^{*} 〉 - Φ (x) = - \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ

where:

(70)

x^{*} = \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ and p_{x} (ξ) = e^{- 〈 ξ, x 〉} / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ = e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} = e^{- 〈 x, ξ 〉 + Φ (x)}

with

(71)

x^{*} = \frac{\partial Φ (x)}{\partial x} and x = \frac{\partial Φ^{*} (x^{*})}{\partial x^{*}}

Souriau introduced these relations in the framework of variational problems to extend them with a covariant definition. Let M be a differentiable manifold with a continuous positive density dω and let E a finite vector space and U(ξ) a continuous function defined on M with values in E. A continuous positive function p(ξ) solution of this problem with respect to calculus of variations:

(72)

\underset{p (ξ)}{A r g M i n} [s = - \int_{M} p (ξ) log p (ξ) d ω] such that {\begin{array}{l} \int_{M} p (ξ) d ω = 1 \\ \int_{M} U (ξ) p (ξ) d ω = Q \end{array}

is given by:

(73)

p (ξ) = e^{Φ (β) - β . U (ξ)} with Φ (β) = - log \int_{M} e^{- β . U (ξ)} d ω and Q = \frac{\int_{M} U (ξ) e^{- β . U (ξ)} d ω}{\int_{M} e^{- β . U (ξ)} d ω}

Entropy $s = - \int_{M} p (ξ) log p (ξ) d ω$ can be stationary only if there exist a scalar Φ and an element β belonging to the dual of E, where Φ and β are Lagrange parameters associated to the previous constraints. Entropy appears naturally as Legendre transform of Φ:

(74)

s (Q) = β . Q - Φ (β)

This value is a strict minimum of s, and the equation $Q = \frac{\int_{M} U (ξ) e^{- β . U (ξ)} d ω}{\int_{M} e^{- β . U (ξ)} d ω}$ has a maximum of one solution for each value of Q. The function Φ(β) is differentiable and we can write dΦ = dβ.Q and identifying E with its dual:

(75)

Q = \frac{\partial Φ}{\partial β}

Uniform convergence of $\int_{M} U (ξ) \otimes U (ξ) e^{- β . U (ξ)} d ω$ proves that $- \frac{\partial^{2} Φ}{\partial β^{2}} > 0$ and that −Φ(β) is convex. Then, Q(β) and β(Q) are mutually inverse and differentiable, where ds = β.dQ.

Identifying E with its bidual:

(76)

β = \frac{\partial s}{\partial Q}

Classically, if we take $U (ξ) = (\begin{matrix} ξ \\ ξ \otimes ξ \end{matrix})$ , components of Q will provide moments of first and second order of the density of probability p(ξ), that is defined by Gaussian law.

Souriau has applied this approach for classical statistical mechanic systems. Considering a mechanical system with n parameters q₁, ···, q_n, its movement could be defined by its phase at arbitrary time t on a manifold of dimension 2n: q₁, ···, q_n, p₁, ···, p_n.

The Liouville theorem shows that coordinate changes have a Jacobian equal to unity, and a Liouville density could be defined on manifold M: dω = dq₁ ···dq_ndp₁ ···dp_n that will not depend on choice to t.

A system state is one point on 2n-Manifold M and a statistical state is a law of probability defined on M such that $\int_{M} p (ξ) d ω (ξ) = 1$ , and its time evolution is driven by:

(77)

\frac{\partial p}{\partial t} = \sum \frac{\partial p}{\partial p_{j}} \frac{\partial H}{\partial q_{j}} - \frac{\partial p}{\partial q_{j}} \frac{\partial H}{\partial p_{j}}

where H is the Hamiltonian.

A thermodynamic equilibrium is a statistical state that maximizes the entropy:

(78)

s = - \int_{M} p (ξ) log p (ξ) d ω

among all states giving the mean value of energy Q:

(79)

\int_{M} H (ξ) . p (ξ) d ω = Q

Applying this for free particles, for an ideal gas, equilibrium is given for $β = \frac{1}{k T}$ (with k being the Boltzmann constant) and if we set S = k.s, the previous relation $d S = \frac{d Q}{T}$ provides: $S = \int \frac{d Q}{T}$ and $S = \int \frac{d Q}{T}$ and Φ (β) is identified with the Massieu-Duhem Potential. We recover also the Maxwell Speed law:

(80)

p (ξ) = c s t e . e^{- \frac{H}{k T}}

The main discovery of Jean-Marie Souriau is that previous thermodynamic equilibrium is not covariant on a relativity point of view. Then, he has proposed a covariant definition of thermodynamic equilibrium where the previous definition is a particular case. In previous formalization, manifold M was solution of the calculus of variations problem:

(81)

d \int_{t_{0}}^{t_{1}} l (t, q_{j}, \frac{{d q}_{j}}{d t}) d t = 0 with p_{j} = \frac{\partial l}{\partial q_{j}}

We can then consider the time variable t like other variables q_j through an arbitrary parameter τ, and define the new calculus of variations problem by:

(82)

d \int_{t_{0}}^{t_{1}} L (q_{J}, {\dot{q}}_{J}) d τ = 0 with t = q_{n + 1}, {\dot{q}}_{J} = \frac{{d q}_{J}}{d τ} and J = 1, 2, \dots, n + 1

where:

(83)

L (q_{J}, {\dot{q}}_{J}) = l (t, q_{j}, \frac{{\dot{q}}_{j}}{\dot{t}}) \dot{t}

Variables p _j are not changed and we have the relation:

(84)

p_{n + 1} = l - \sum_{j} p_{j} . \frac{{d q}_{j}}{d t}

If we compare with classical mechanic, we have:

(85)

p_{n + 1} = - H with H = \sum_{j} p_{j} . \frac{{d q}_{j}}{d t} - l (H is Legendre transform of l)

H is the energy of the system that is conservative if the Lagrangian doesn’t depend explicitly of time t. It is a particular case of Noether Theorem:

If Lagrangian L is invariant by an infinitesimal transform dQ_J = F_J(Q_K), then $u = \sum_{J} p_{J} {d Q}_{J}$ first integral of variations equations.

As energy is not the conjugate variable of time t, or the value provided by Noether theorem by system invariance to time translation, the thermodynamic equilibrium is not covariant. Then, Souriau proposes a new covariant definition of thermodynamic equilibrium:

Let a mechanical system with a Lagrangian invariant by a Lie Group G. Equilibrium states by Group G are statistical states that maximizes the Entropy, while providing given mean values to all variables associated by Noether theorem to infinitesimal transforms of group G.

Neither theorem allows associating to all system movement ξ, a value U(ξ) belonging to the vector space dual of Lie Algebra ℊ of group G. U(ξ) is called the moment of the group.

For each derivation δ of this Lie algebra [83], we take:

(86)

U (ξ) (δ) = \sum_{J} p_{J} . δ Q_{J}

With previous development, as ℊ^* is dual of ℊ, value β belongs to this Lie algebra ℊ, geometric generalization of thermodynamic temperature. Value Q is a geometric generalization of heat and belongs to ℊ^*, the dual of ℊ.

An Equilibrium state exists having the largest entropy, with a distribution function p(ξ) that is the exponential of an affine function of U [83]:

(87)

p (ξ) = e^{Φ (β) - β . U (ξ)} with Φ (β) = - log \int_{M} e^{- β . U (ξ)} d ω and Q = \frac{\int_{M} U (ξ) e^{- β . U (ξ)} d ω}{\int_{M} e^{- β . U (ξ)} d ω}

with:

(88)

s (Q) = β . Q - Φ (β), d Φ = d β . Q and d s = β . d Q

A statistical state p(ξ) is invariant by δ if δ[p(ξ)] = 0 for all ξ (then p(ξ) is invariant by finite transform of G generated by δ).

Jean-Marie Souriau gave the following theorem:

Souriau Theorem 1

An equilibrium state allowed by a group G is invariant by an element δ of Lie Algebra ℊ, if and only if [δ,β] = 0 (with [.], the Lie Bracket), with β the generalized equilibrium temperature.

For classical thermodynamic, where G is an Abelian group of translation with respect to time t, all equilibrium states are invariant under G. For Group of transformation of Space-Time, elements of Lie Algebra of G could be defined as vector fields in Space-Time. The generalized temperature β previously defined, would be also defined as a vector field. For each point of manifold M, we could then define:

Temperature Vector:
(89) $β_{M} = \frac{V}{k T}$
with:
Unitary Mean Speed:
(90) $Unitary Mean Speed : V = \frac{β_{M}}{‖ β_{M} ‖} with ‖ V ‖ = 1$
Eigen Absolute Temperature:
(91) $T = \frac{1}{k . ‖ β_{M} ‖}$

Classical formula of thermodynamics are thus generalized, but variables are defined with a geometrical status, like the geometrical temperature β_M an element of the Lie algebra of the Galileo or Poincaré groups, interpreted as the field of space-time vectors. Souriau proved that in relativistic version β_M is a time like vector with an orientation that characterizes the arrow of time. The temperature vector and entropy flux are in duality. Souriau said “β, c’est la flèche qui nous indique dans quel sens coule le temps” [β, it is the arrow that informs about the flow of time direction].

5. Souriau-Gibbs Canonical Ensemble of Dynamical Group and Lie Group Thermodynamics

In statistical mechanics, a canonical ensemble [117–121] is the statistical ensemble that is used to represent the possible states of a mechanical system that is being maintained in thermodynamic equilibrium. Souriau has defined this Gibbs canonical ensemble on Symplectic manifold M for a Lie group action on M.

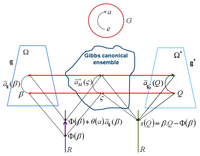
In classical statistical mechanics, a state is given by the solution of Liouville equation on the phase space, the partition function. The seminal idea of Lagrange was to consider that a statistical state is simply a probability measure on the manifold of motions, as in the Souriau approach, where one movement of a dynamical system (classical state) is a point on manifold of movements. For statistical mechanics, the movement variable is replaced by a random variable where a statistical state is probability law on this manifold. As symplectic manifolds have a completely continuous measure, invariant by diffeomorphisms, the Liouville measure λ, all statistical states will be the product of Liouville measure by the scalar function given by the generalized partition function e^Φ−^β^.^U defined by the generalized energy U (the moment that is defined in dual of Lie Algebra of this dynamical group) and the geometric temperature β, where Φ is a normalizing constant such the mass of probability is equal to 1, $Φ = - log \int_{M} e^{- β . U} d ω$ . Souriau then generalizes the Gibbs equilibrium state to all symplectic manifolds that have a dynamical group. To ensure that all integrals, that will be defined, could converge, the canonical Gibbs ensemble is the largest open proper subset (in Lie algebra) where these integrals are convergent. This canonical Gibbs ensemble is convex. The derivative of $Q = \frac{\partial Φ}{\partial β}$ is equal to the mean value of the energy U (heat in thermodynamic). The minus derivative of this generalized heat Q, $- \frac{\partial Φ}{\partial β}$ is symmetric and positive (it is a generalization of heat capacity). Entropy s is then defined by Legendre transform of Φ, s = β.Q−Φ. If this approach is applied for the group of time translation, this is the classical thermodynamic theory. But Souriau has observed that if we apply this theory for non-commutative group (Galileo or Poincaré groups), the symmetry has been broken. Classical Gibbs equilibrium states are no longer invariant by this group. This symmetry breaking provides new equations, discovered by Souriau.

For each temperature β, Souriau has introduced a tensor f_β, equal to the sum of cocycle f and Heat coboundary (with [.,.] Lie bracket):

(92)

f_{β} (Z_{1}, Z_{2}) = f (Z_{1}, Z_{2}) + Q . A d_{Z_{1}} (Z_{2}) with A d_{Z_{1}} (Z_{2}) = [Z_{1}, Z_{2}]

This tensor f_β has the following properties:

f is a symplectic cocycle (we refer to books of Sympectic geometry for cocycle definition)
β ∈ Ker f_β
The following symmetric tensor g_β, defined on all values of Ad_β(.) is positive definite:
(93) $g_{β} ([β, Z_{1}], [β, Z_{2}]) = f_{β} (Z_{1}, [β, Z_{2}])$

These equations are universal, because they are not dependent of the symplectic manifold but only of the dynamical group G, its symplectic cocycle f, the temperature β and the heat Q. Souriau called this model “Lie Groups Thermodynamics”. We can read in his paper this prophetical sentence “Peut-être cette thermodynamique des groups de Lie a-t-elle un intérêt mathématique”[Maybe this thermodynamics of Lie groups has a mathematical interest]. He explains that for dynamic Galileo group (rotation and translation) with only one axe of rotation, this thermodynamic theory is the theory of centrifuge where the temperature vector dimension is equal to 2 (sub-group of invariance of size 2), used to make “butter”, “uranium 235” and “ribonucleic acid”. The physical meaning of these 2 dimensions for vector-valued temperature are “thermic conduction” and “viscosity”. Souriau said that the model unifies “heat conduction” and “viscosity” (Fourier and Navier equations) in the same theory of irreversible process. Souriau has applied this theory in details for relativistic ideal gas with Poincaré group for dynamical group.

We will give in the following the two others main theorems of Souriau on this Lie Group Thermodynamics.

Souriau Theorem 2

Let Ω be the largest open proper subset of ℊ, Lie algebra of G, such that $\int_{M} e^{- β . U (ξ)} d ω$ and $\int_{M} ξ . e^{- β . U (ξ)} d ω$ are convergent integrals, this set Ω is convex and is invariant under every transformation ā_ℊ, where a↦ā_ℊ is the adjoint representation of G. Then, the variables are changed according to:

(94)

β \to {\bar{a}}_{g} (β)

(95)

Φ \to Φ - θ (a^{- 1}) β = Φ + θ (a) . {\bar{a}}_{g} (β)

(96)

s \to s

(97)

Q \to {\bar{a}}_{g^{*}} (Q) + θ (a) = {\bar{a}}_{g_{θ}^{*}} (Q)

(98)

ς \to {\bar{a}}_{M}^{+} (ς)

where θ is the cocycle associated with the group G and the moment, and ${\bar{a}}_{M}^{+} (ς)$ is the image under ā_M of the probability measure ς.

We observe that the entropy s is unchanged, and Φ is changed but with linear dependence to β, with consequence that Fisher Information Geometry metric is unchanged by the dynamical group:

(99)

I ({\bar{a}}_{g} (β)) = - \frac{\partial^{2} [Φ - θ (a^{- 1}) β]}{\partial β} = - \frac{\partial^{2} Φ}{\partial β^{2}} = I (β)

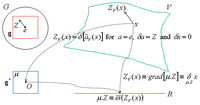
These transformations have been geometrically interpreted by Souriau in Figure 4:

In previous notation, a↦ā_ℊ the adjoint representation of G can be written:

(100)

{\bar{a}}_{g} (Z) = δ [a \times b \times a^{- 1}] with b = e, δ b = Z and δ a = 0

a↦a_ℊ defines an action of G on its Lie algebraℊ, with ā_ℊ is called the adjoint representation, that is a linear representation of G on its Lie algebra ℊ.

Let a be an arbitrary element of G and ā_M action of a on the manifold M. Since ${\bar{a}}_{M}^{- 1}$ symplectomorphism, the image under ${\bar{a}}_{M}^{- 1}$ of the Liouville measure λ is equal to λ. The integral $\int_{M} e^{- β . U (ξ)} . d ω$ is equal with invariance property of Liouville measure to the integral $\int_{M} e^{- β . U ({\bar{a}}_{M}^{- 1} (ξ))} . d ω$ :

(101)

\int_{M} e^{- β . U (ξ)} . d ω = \int_{M} e^{- β . U ({\bar{a}}_{M}^{- 1} (ξ))} . d ω

We can then use the following relation:

(102)

U ({\bar{a}}_{M}^{- 1} (ξ)) = {\bar{a}}_{g^{*}}^{- 1} (U (ξ)) + θ (a^{- 1})

with θ a symplectic cocycle of G. This cocycle is defined for:

(103)

\begin{array}{l} U : M \to g^{*} \\ ξ \mapsto μ \end{array}

there exist then a differential map θ defined by:

(104)

\begin{array}{l} θ : G \to g^{*} \\ a \mapsto U ({\bar{a}}_{M} (ξ)) - {\bar{a}}_{g^{*}} (U (ξ)) \end{array}

This differential map θ satisfy the condition:

(105)

θ (a \times b) = θ (a) + {\bar{a}}_{g^{*}} (θ (b))

and its derivative f = D(θ)(e) where e is the identity element of G, is a 2-form on the Lie algebra ℊ of G which satisfies:

(106)

f (Z_{1}, [Z_{2}, Z_{3}]) + f (Z_{2}, [Z_{3}, Z_{1}]) + f (Z_{3}, [Z_{1}, Z_{2}]) = 0, \forall Z_{1}, Z_{2} Z_{3} \in g

and the following identities:

(107)

D (U) (ξ, Z_{M} (ξ)) = U (ξ) . A d_{Z} (.) + f (Z, Z)

where Z_M(ξ) is the fundamental vector field on the manifold M associated to Z ∈ ℊ :

(108)

Z_{M} (ξ) = δ [{\bar{a}}_{M} (ξ)] for a = e, δ a = Z and δ ξ = 0

(109)

σ (Z_{1, M} (ξ), Z_{2, M} (ξ)) = μ . [Z_{1}, Z_{2}] + f (Z_{1}, Z_{2})

with σ the Lagrange form.

If we use previous relation $U ({\bar{a}}_{M}^{- 1} (ξ)) = {\bar{a}}_{g^{*}}^{- 1} (U (ξ)) + θ (a^{- 1})$ , and the property that ${\bar{a}}_{g^{*}} (U (ξ)) = U (ξ) . {\bar{a}}_{g}^{- 1}$ , by defining:

(110)

β^{'} = {\bar{a}}_{g} (β)

the integral is then defined by:

(111)

\int_{M} e^{- β^{'} . U (ξ)} . d ω = \int_{M} e^{- {\bar{a}}_{g} (β) . U ({\bar{a}}_{M}^{- 1} (ξ))} . d ω = \int_{M} e^{- {\bar{a}}_{g} (β) . [{\bar{a}}_{g^{*}}^{- 1} (U (ξ)) + θ (a^{- 1})]} . d ω = e^{θ (a^{- 1}) . β} \int_{M} e^{- β . U (ξ)} . d ω

We can then deduce the equation of Souriau theorem on Φ:

(112)

Φ^{'} = Φ (β^{'}) = Φ ({\bar{a}}_{g} (β)) = - log \int_{M} e^{- β^{'} . U (ξ)} . d ω = - log (e^{θ (a^{- 1}) . β} \int_{M} e^{- β . U (ξ)} . d ω) = Φ (β) - θ (a^{- 1}) β

The equation of Souriau theorem on Q uses the relation ${\bar{a}}_{g^{*}} (Q) = Q . {\bar{a}}_{g}^{- 1}$ :

(113)

Φ^{'} = Φ (β^{'}) = Φ ({\bar{a}}_{g} (β)) = - log \int_{M} e^{- β^{'} . U (ξ)} . d ω = - log (e^{θ (a^{- 1}) . β} \int_{M} e^{- β . U (ξ)} . d ω) = Φ (β) - θ (a^{- 1}) β

Finally, using ${\bar{a}}_{g^{*}} (Q) = Q . {\bar{a}}_{g}^{- 1}$ , we can prove that the Entropy is invariant:

(114)

s^{'} = β^{'} . Q^{'} - Φ^{'} = {\bar{a}}_{g} (β) . ({\bar{a}}_{g} . (Q) + θ (a)) - (Φ + θ (a) {\bar{a}}_{g} (β)) = {\bar{a}}_{g} (β) . {\bar{a}}_{g} . (Q) - Φ = {\bar{a}}_{g}^{.1} {\bar{a}}_{g} (β) . Q - Φ = β . Q - Φ = s

Considering the density of probability p_β(ξ) = e⁻^β^.^U⁽^ξ^{) + Φ(}^β⁾ with β′ = ā_ℊ (β), then: p_β_′(ξ) = e⁻^ā^_ℊ^β^.^U⁽^ξ^{) + Φ(}^β⁾⁻^θ⁽^a⁻¹)^β.

From which, we can recover ${\bar{a}}_{M}^{+}$ the image under ā_M of the probability measure.

The last Souriau theorem is given by:

Souriau Theorem 3

Let f = D(θ)(e) be the derivative of θ (symplectic cocycle of G) at the identity element and let us define:

(115)

\forall β \in Ω, f_{β} (Z_{1}, Z_{2}) = f (Z_{1}, Z_{2}) + Q . A d_{Z_{1}} (Z_{2}) with A d_{Z_{1}} (Z_{2}) = [Z_{1}, Z_{2}]

Then

f_β is a symplectic cocycle of ℊ, that is independent of the moment of G

(116)

f_{β} (β, β) = 0, \forall β \in Ω (β \in K e r f_{β})

There exists a symmetric tensor g_β defined on the image of Ad_β(.) = [.,β] such that:
(117) $g_{β} ([β, Z_{1}], Z_{2}) = f_{β} (Z_{1}, Z_{2}), \forall Z_{1} \in g, \forall Z_{2} \in Im (A d_{β} (.))$
and:
(118) $g_{β} (Z_{1}, Z_{2}) \geq 0, \forall Z_{1}, Z_{2} \in Im (A d_{β} (.))$
Last equation gives the structure of a positive Euclidean space.

f_β(β, β) = 0 could be deduced by differentiating Φ(ā_ℊ (β)) = Φ + θ(a).ā_ℊ (β) and taking a = e, δa = Z₂ and δZ₁ = 0. As Z_M(ξ) = δ[ā_M (ξ)] and Z_ℊ = −Ad_Z(.), we have Q[Z₁,Z₂] = −f (Z₁,Z₂).

If we differentiate Q(ā_ℊ(β)))ā_ℊ_*(Q) + θ(a), the following relation $\frac{\partial Q}{\partial β} (- [Z_{1}, β]) = f (Z_{1}, Z_{1}) + Q . A d_{Z_{1}} (.) = f_{β} (Z_{1}, Z_{1})$ appears. Then, writing δβ = [β,Z₁] = Z₂, we have δQ.δβ ≥ 0 ⇒ f_β(Z₁, Z₂) ≥ 0.

See more details in appendix A.3.

6. Synthesis of Analogies Between the Koszul Information Geometry Model and Souriau Statistical Physics Model

6.1. Comparison of Koszul and Souriau Models

We will synthetize in Table 1 results of previous chapters with Koszul Hessian Structure of Information Geometry and the Souriau model of Statistical Physics with the general concepts of geometric temperature, heat and capacity. Analogies between models will deal with characteristic function, Entropy, Legendre Transform, density of probability, dual coordinate systems, Hessian Metric and Fisher metric.

As $Q = \frac{\partial Φ}{\partial β}$ , we observe that the Information Geometry metric $I (β) = - \frac{\partial^{2} Φ (β)}{\partial β^{2}} = - \frac{\partial Q}{\partial β}$ could be considered as a generalization of “Heat Capacity”. Souriau called it K the “Geometric Capacity”. When $β = \frac{1}{k T}, K = - \frac{\partial Q}{\partial β} = - \frac{\partial Q}{\partial T} (\frac{\partial \frac{1}{k T}}{\partial T}) = \frac{1}{k T^{2}} \frac{\partial Q}{\partial T}$ , then this geometric capacity is related to calorific capacity. Q is related to the mean, and K is related to the variance of U [122]:

(119)

I (β) = - \frac{\partial Q}{\partial β} = var (U) = \int_{M} U {(ξ)}^{2} . p_{β} (ξ) d ω - {(\int_{M} U (ξ) . p_{β} (ξ) d ω)}^{2}

6.2. Invariances in Koszul and Souriau Models

We have observed in previous chapters the main invariances characterizing the Koszul Model and the Souriau Model. We will synthetize these invariances in Table 2.

In both the Koszul and Souriau models, the Information Geometry Metric and the Entropy are invariant respectively to the automosphisms g of the convex cone Ω and to ā_ℊ adjoint representation of Dynamical group G acting on Ω, the convex cone considered as largest open subset of ℊ, Lie algebra of G, such that $\int_{M} e^{- β . U (ξ)} d ω$ and $\int_{M} ξ . e^{- β . U (ξ)} d ω$ are convergent integrals.

6.3. Souriau Thermometer

Souriau has built a thermometer (θɛρμός) device principle that could measure the Geometric Temperature using “Relative Ideal Gas Thermometer” based on a theory of Dynamical Group Thermometry, and has also recovered the Laplace barometric law p(⇉) ∝ e⁻^mβ^〈^g⃗^,^⇉^〉.

7. From Characteristic Function to Generative Inner Product

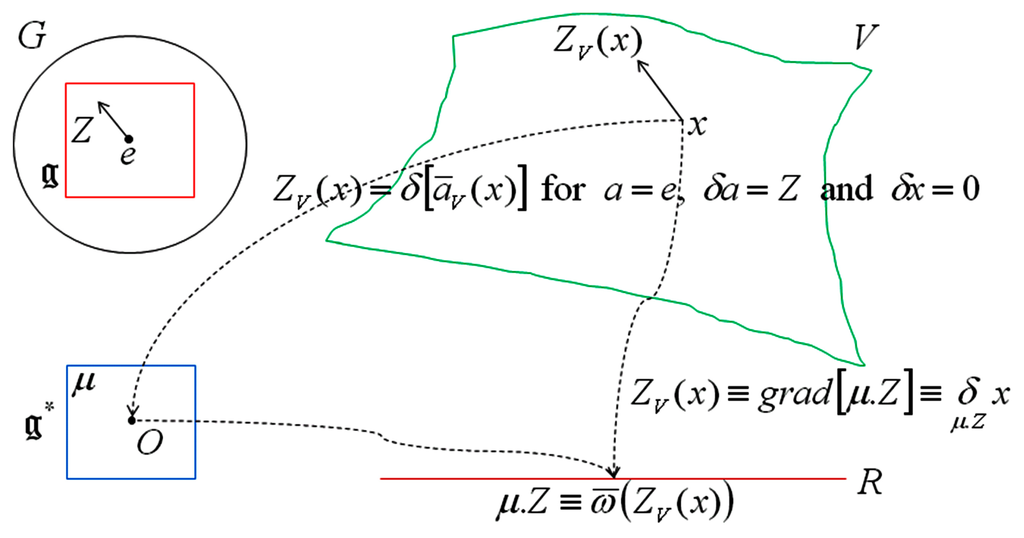
Cartan’s works have greatly influenced Koszul (Koszul’s PhD thesis extended previous work of Cartan) and Souriau (Souriau was a student of Elie Cartan at ENS, the year after his aggregation). We have shown that “Information Geometry” could be considered as a particular application domain of Hessian Geometry through Koszul’s work (Koszul-Vinberg metric deduced from the associated characteristic function having the main property of being invariant to all automorphisms of the convex cone), that could be extended in the framework of Souriau’s theory, as an extension towards “Lie Group Thermodynamics” with vector-valued geometric temperature (providing a geometric extension of Noether’s theorem). Should we deduce that the “essence” of Information Geometry is limited to the “Koszul Characteristic Function”? This notion seems to not be the more general one, and we will explore the notion of Generative Inner Products. We will reduce Koszul’s and Souriau’s definitions to exclusive “Inner Product” selection using symmetric bilinear “Cartan-Killing form” introduced by Cartan in 1894.

In Koszul Geometry, we have two convex dual functions Φ(x) and Φ^*(x^*) with dual system of coordinates x and x^* defined on dual cones Ω and Ω^* : $Φ (x) = - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \forall x \in Ω$ and Φ^* (x^* ) = 〈x, x^*〉 –Φ(x). We can then remark that if we can define an Inner Product 〈.,.〉, we will be able to build a convex function Φ(x) = −log ψ_Ω (x) and its dual by Legendre transform because both are only dependent of the Inner product, and dual coordinate is also defined by $x^{*} = arg min {ψ_{Ω} (y) / y \in Ω^{*}, 〈 x, y 〉 = n} = \int_{Ω^{*}} ξ . e^{- 〈 ξ, x 〉} d ξ / \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ$ where x^* is also the center of gravity of the cross section {y ∈ Ω^*, 〈x, y〉 = n} of Ω^* (with notation: Φ(x) = −logψ_Ω(x)).

It is not possible to define an ad(g)-invariant inner product for any two elements of a Lie Algebra, but a symmetric bilinear form, called “Cartan-Killing form”, could be introduced. This form has been introduced first by Cartan in 1894 in his PhD thesis. This form is defined according to the adjoint endomorphism Ad_x of g that is defined for every element x of g with the help of the Lie bracket:

(120)

A d_{x} (y) = [x, y]

The trace of the composition of two such endomorphisms defines a bilinear form, the Cartan-Killing form:

(121)

B (x, y) = T r (A d_{x} A d_{y})

The Cartan-Killing form is symmetric:

(122)

B (x, y) = B (y, x)

and has the associativity property:

(123)

B ([x, y], z) = B (x, [y, z])

given by:

(124)

B ([x, y], z) = T r (A d_{[x, y]} A d_{z}) = T r ([A d_{x}, A d_{y}] A d_{z}) = T r (A d_{x} [A d_{y}, A d_{z}]) = B (x, [y, z])

Elie Cartan has proved that if g is a simple Lie algebra (the Killing form is non-degenerate) then any invariant symmetric bilinear form on g is a scalar multiple of the Cartan-Killing form. The Cartan-Killing form is invariant under automorphisms σ ∈ Aut(g) of the algebra g:

(125)

B (σ (x), σ (y)) = B (x, y)

To prove this invariance, we have to consider:

(126)

{\begin{array}{l} σ [x, y] = [σ (x), σ (y)] \\ z = σ (y) \end{array} \Rightarrow σ [x, σ^{- 1} (z)] = [σ (x), z] rewritten A d_{σ (x)} = σ \circ A d_{x} \circ σ^{- 1}

Then:

(127)

B (σ (x), σ (y)) = T r (A d_{σ (x)} A d_{σ (y)}) = T r (σ \circ A d_{x} A d_{y} \circ σ^{- 1}) = T r (A d_{x} A d_{y}) = B (x, y)

A natural G-invariant inner product could be then introduced by Cartan-Killing form. Cartan Generative Inner Product: The following Inner product defined by Cartan-Killing form is invariant by automorphisms of the algebra

(128)

〈 x, y 〉 = - B (x, θ (y))

where θ ∈ g is a Cartan involution (an involution on g is a Lie algebra automorphism θ of g whose square is equal to the identity).

From the Cartan Inner Product, we can generate logarithm of the Koszul Characteristic Function, and its Legendre Transform to define Koszul Entropy, Koszul Density and Koszul Metric, as explained in the following Figure 5:

In Appendix A2, we give the definition of another inner product, Gromov Inner product, in CAT(−1) space, that could be also used to generalize Koszul definition of Characteristic Function.

On the concept of generative structure, we could also explore the notion of Generative Function [123–126] and come back to seminal paper of Chentsov about axiomatization of Information Geometry [127].

8. Conclusions on General Definition of Entropy by Legendre Transform

Definition of Entropy has been widely debated [128,129]. Based on the cornerstone concept of the Koszul Vinberg Characteristic Function, we have introduced Koszul Entropy as the Legendre transform of its logarithm. This definition of Entropy could be extended by interpretating Legendre transform as Fourier transform in (Min,+) algebra [130,131].

As we have observed previously, Koszul Entropy has a Shannon Entropy structure:

(129)

\begin{array}{l} Φ^{*} (x^{*}) = Φ^{*} (E [ξ]) = - \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ = \int_{Ω^{*}} Φ^{*} (ξ) p_{x} (ξ) d ξ = E [Φ^{*} (ξ)] \\ with Φ^{*} (ξ) = - log p_{x} (ξ) and x^{*} = \int_{Ω^{*}} ξ . p_{x} (ξ) d ξ = E [ξ] \\ where p_{x} (ξ) = \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} = e^{- 〈 x, ξ 〉 - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ} = e^{- 〈 x, ξ 〉 + Φ (x)} \end{array}

In last equation, variable x could be defined by ξ̄ = E[ξ] = x^* if function $\frac{d Φ (x)}{d x}$ could be inverted:

(130)

p_{\bar{ξ}} (ξ) = \frac{e^{- 〈 ξ, Θ^{- 1} (\bar{ξ}) 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, Θ^{- 1} (\bar{ξ}) 〉} d ξ} with x = Θ^{- 1} (\bar{ξ}) and \bar{ξ} = Θ (x) = \frac{d Φ (x)}{d x}

where:

(131)

\bar{ξ} = \int_{Ω^{*}} ξ . p_{\bar{ξ}} (ξ) d ξ and Φ (x) = - log \int_{Ω^{*}} e^{- 〈 x, ξ 〉} d ξ

In previous chapters, a definition of Koszul Entropy Φ^*(x^*) through Legendre transform of Koszul-Vinberg characteristic function Φ (x) has been given:

(132)

\begin{array}{l} Φ^{*} (x^{*}) = 〈 x, x^{*} 〉 - Φ (x) \\ with Φ (x) = - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \forall x \in Ω \end{array}

where Φ(x) could be interpreted as opposite of logarithm of Laplace transform [132,133]:

(133)

E n t r o p y = L e g e n d r e [- log [L a p l a c e]]

that we will write synthetically as:

(134)

E n t = - L e g \circ L o g \circ L a p l

The function Leg ○ Log ○ Lapl is sometimes called “Cramer transform”.

If we remark that the Legendre transform is closely related to the idempotent analogue of the Fourier transform [130,131,134–136], we could then give a new definition of Entropy.

If we consider the semiring R_min = R ∪ {+∞} with the operations ⊕ = Min and • = +. In R_min = R ∪ {+∞} the idempotent analogues of integration on R^N is given by the formula:

(135)

I (f) = \int_{R^{N}}^{\oplus} f (x) d x = \underset{x \in R^{N}}{I n f} f (x)

Then, the Legendre transform is equivalent to the Fourier transform in (⊕,•) = (Min,+) algebra [130]:

(136)

Φ^{*} (ξ) = \underset{x \in Ω}{S u p} [〈 x, ξ 〉 - Φ (x)] = - \int_{Ω}^{\oplus} (- 〈 x, ξ 〉) • Φ (x) d x = F o u r_{(M i n, +)} [Φ (x)]

The Legendre transform generates an idempotent version of harmonic analysis for the space of convex functions. We can then give a general definition of Entropy:

(137)

E n t = - F o u r_{(M i n, +)} \circ L o g \circ L a p l_{(+, \times)}

We can also observe the following properties deduced from the Laplace and Legendre transforms’ characteristics:

(138)

E n t (μ \otimes γ) = E n t (μ) • E n t (γ)

where * is the convolution operator and ⊗ the inf-convolution operator (see [130] for the definition of inf-convolution) defined by:

(139)

[f • g] (z) = \underset{x}{I n f} [f (x) + g (y - x)]

with f and g, two functions R→R_min.

“La théorie cinétique des gaz laisse encore subsister bien des points embarrassants pour ceux qui sont accoutumés à la rigueur mathématique… L’un des points qui m’embarrassaient le plus était le suivant: il s’agit de démontrer que l’entropie va en diminuant, mais le raisonnement de Gibbs semble supposer qu’après avoir fait varier les conditions extérieures on attend que le régime soit établi avant de les faire varier à nouveau. Cette supposition est-elle essentielle, ou en d’autres termes, pourrait-on arriver à des résultats contraires au principe de Carnot en faisant varier les conditions extérieures trop vite pour que le régime permanent ait le temps de s’établir? ”
Henri Poincaré « Réflexions sur la théorie cinétique des gaz », 1906
[The kinetic theory of gases leaves awkward points for those who are accustomed to mathematical rigor … One of the points which embarrassed me most was the following one: it is a question of demonstrating that the entropy keeps decreasing, but the reasoning of Gibbs seems to suppose that having made vary the outside conditions we wait that the regime is established before making them vary again. Is this supposition essential, or in other words, we could arrive at opposite results to the principle of Carnot by making vary the outside conditions too fast so that the permanent regime has time to become established ?]
Henri Poincaré “Reflection on The kinetic theory of gases”, 1906
“Quel est l'objet de l’art ? Si la réalité venait frapper directement nos sens et notre conscience, si nous pouvions entrer en communication immédiate avec les choses et avec nous-mêmes, je crois bien que l’art serait inutile, ou plutôt que nous serions tous artistes, car notre âme vibrerait alors continuellement à l’unisson de la nature. ”
Henri Bergson, Le rire, p.115, Éd. P.U.F
[What is the object of art? Could reality come into direct contact with sense and consciousness, could we enter into immediate communion with things and with ourselves, probably art would be useless, or rather we should all be artists, for then our soul would continually vibrate in perfect accord with nature.]
Henri Bergson, Laughter

Acknowledgments

Many thanks are due to members of the Leon Brillouin seminar with very fruitful discussions on Geometric Science of Information and Information Geometry, initiated since December 2009. Souriau Models were more clearly understood with the help of Claude Vallée that sent me unpublished chapters of Souriau’s book [86]. Jean-Louis Koszul has participated to the first GSI conference at Ecole des Mines in 2013, where Hirohiko Shima gave a keynote lecture on Koszul Hessian Geometry.

Appendix

A1. Legendre Transform and Minimal Surface

Laplace contribution to probability was around 1774 [137]. At almost the same period, in 1787, Adrien-Marie Legendre has introduced the “Legendre Transform” [138] to solve the Minimal Surface Problem equation introduced by Lagrange and partially solved by Gaspard Monge in 1784 [139]. In 1768, Lagrange considered the variational problem of least area surface stretched across a given closed contour. Based on Euler-Lagrange equation, Lagrange has introduced the equation of Minimal Surface z(x, y):

(140)

(1 + q^{2}) \frac{d^{2} z}{{d x}^{2}} - 2 p q \frac{d^{2} z}{d x d y} + (1 + p^{2}) \frac{d^{2} z}{{d y}^{2}} = 0 with \frac{d z}{d x} = p and \frac{d z}{d y} = q

Lagrange has observed that affine functions z(x,y) = a.x + b.y + c are solutions of this equation and minimal surfaces are planes.

Jean-Baptiste Marie Meusnier de La Place, a student of Monge, has observed that for this surface, two curvature radiuses are everywhere equal but directed in opposite direction, because first equation is equal to two times the mean curvature H_z:

(141)

2 H_{z} = \frac{d}{d x} (\frac{\frac{d z}{d x}}{\sqrt{1 + {(\frac{d z}{d x})}^{2} + {(\frac{d z}{d y})}^{2}}}) + \frac{d}{d y} (\frac{\frac{d z}{d y}}{\sqrt{1 + {(\frac{d z}{d x})}^{2} + {(\frac{d z}{d y})}^{2}}}) = \frac{(1 + q^{2}) \frac{d^{2} z}{{d x}^{2}} - 2 p q \frac{d^{2} z}{d x d y} + (1 + p^{2}) \frac{d^{2} z}{{d y}^{2}}}{{(1 + {(\frac{d z}{d x})}^{2} + {(\frac{d z}{d y})}^{2})}^{3 / 2}}

Gaspard Monge integrated this equation in [139] but with a non-rigorous approach and asked Legendre to find a more classical solution. For this task, Legendre has introduced a change of variable that is the nowadays well-known “Legendre transform”. Adrien-Marie Legendre said “J’y suis parvenu simplement par un changement de variables qui peut être utile dans d’autres occasions”(“I reached there simply by a change of variables which can be useful in other opportunities”).

Legendre reduced the problem to solve to determine p and q as functions of x and y such that:

(142)

p . d x + q . d y and \frac{p . d y - q . d x}{\sqrt{1 + p^{2} + q^{2}}}

are exact differentials. If we set 1 + p² + q² = u², then these other expressions are complete differentials:

(143)

x . d p + y . d q and y . d (\frac{p}{u}) + x . d (\frac{q}{u})

Legendre considered x and y as functions of p and q:

(144)

x . d p + y . d q = d ω with x = \frac{d ω}{d p} and y = \frac{d ω}{d q}

If we then develop $y . d (\frac{p}{u}) + x . d (\frac{q}{u})$ , we have:

(145)

[(1 + q^{2}) y + p q . x] \frac{d p}{u^{3}} - [(1 + p^{2}) x + p q . y] \frac{d q}{u^{3}}

That should be an exact differential. By replacing x and y, we have a new equation:

(146)

(1 + q^{2}) \frac{d^{2} ω}{d q^{2}} + 2 p q . \frac{d^{2} ω}{d p d q} + (1 + p^{2}) \frac{d^{2} ω}{{d p}^{2}} = 0

This new equation is very similar to the previous one, but simpler because it depends on p and q and not their partial differentials of first order. When the function ω will be known, then functions x, y and z will be also defined according to p and q thanks to “Legendre transform”:

(147)

\begin{array}{l} z (x, y) = p . x + q . y - ω (p, q) \\ with x = \frac{d ω}{d p} and y = \frac{d ω}{d q} \end{array}

About this Legendre transform, Darboux [140] gave an interpretation by Chasles “Ce qui revient suivant une remarque de M. Chasles, à substituer à la surface sa polaire réciproque par rapport à un paraboloïde” [What is equivalent according to M. Chasles’s remark, to substitute for the surface its mutual polar with regard to a paraboloid]. This equation could be also written as classical “Legendre transform” with our previous notations:

(148)

\begin{array}{l} s (Q) = β . Q - Φ (β) = 〈 β, Q 〉 - Φ (β) \\ with {\begin{array}{l} Φ (β) = z (x, y) \\ s (Q) = ω (p, q) \end{array}, {\begin{array}{l} Q = [\begin{matrix} Q_{1} \\ Q_{2} \end{matrix}] = [\begin{matrix} p \\ q \end{matrix}] \\ β = [\begin{matrix} β_{1} \\ β_{2} \end{matrix}] = [\begin{matrix} x \\ y \end{matrix}] \end{array} and {\begin{array}{l} Q = [\begin{matrix} \frac{d Φ}{d β_{1}} \\ \frac{d Φ}{d β_{2}} \end{matrix}] = \frac{d Φ}{d β} \\ β = [\begin{matrix} \frac{d s}{{d Q}_{1}} \\ \frac{d s}{{d Q}_{2}} \end{matrix}] = \frac{d s}{d Q} \end{array} \end{array}

In the following relation, we recover the definition of Entropy $d s = β . d Q = \frac{d Q}{T}$ :

(149)

{\begin{array}{l} x . d p + y . d q = d ω \\ x = \frac{d ω}{d p} and y = \frac{d ω}{d q} \end{array} \Rightarrow {\begin{array}{l} β . d Q = d s \\ β = \frac{d s}{d Q} \end{array}

The equation of the surface is characterized by the following equation:

(150)

\frac{d}{d β} (\frac{Q}{\sqrt{1 + ‖ Q | |^{2}}}) = \frac{d}{d β} (\frac{\frac{d Φ}{d β}}{\sqrt{1 + {‖ \frac{d Φ}{d β} ‖}^{2}}}) = 2. H_{Φ} or d i v_{β} (\frac{Q}{\sqrt{1 + ‖ Q | |^{2}}}) = d i v_{β} (\frac{\nabla Φ}{\sqrt{1 + {‖ \nabla Φ ‖}^{2}}}) = 2. H_{Φ}

We can then observed that when ||Q|| << 1, $\frac{d}{d β} (\frac{Q}{\sqrt{1 + {‖ Q ‖}^{2}}}) \approx \frac{d Q}{d β} = - I (β) = 2. H_{Φ}$ .

We can also characterized Entropy with this 2nd equation:

(151)

(1 + Q_{2}^{2}) \frac{d^{2} s (Q)}{d Q_{2}^{2}} + 2 p q . \frac{d^{2} s (Q)}{{d Q}_{1} {d Q}_{2}} + (1 + Q_{1}^{2}) \frac{d^{2} s (Q)}{d Q_{1}^{2}} = 0

We can also find direct equations for x, y and z, based on “Legendre transform” and Equation (146):

(152)

(1 + q^{2}) \frac{d^{2} x}{d q^{2}} + 2 p q . \frac{d^{2} x}{d p d q} + (1 + p^{2}) \frac{d^{2} x}{{d p}^{2}} + 2 q \frac{d x}{d p} + 2 p \frac{d x}{d q} = 0

We have exactly same equations for y and z.

Legendre then solved Equations (145) and (148), by determining two constants a and b given by double integral of the equation:

(153)

(1 + q^{2}) {d p}^{2} - 2 p q . d p . d q + (1 + p^{2}) {d p}^{2} = 0

By selecting p = aq + A with a and A two constants. Previous equation gives 1 + a² + A² = 0. Then a will be let an arbitrary function and $A = \pm \sqrt{- 1 - a^{2}}$ . Two integrals of Equation (129) will be:

(154)

{\begin{array}{l} p = a q + \sqrt{- 1 - a^{2}} = a q + A \\ p = b q - \sqrt{- 1 - b^{2}} = b q + B \end{array}

with a and b two arbitrary constants, roots of the following Equation:

(155)

\begin{array}{l} (1 + q^{2}) v^{2} - 2 p q .. v + (1 + p^{2}) = 0 \\ with {\begin{array}{l} a + b = \frac{2 p q}{1 + q^{2}} \\ a b = \frac{1 + p^{2}}{1 + q^{2}} \end{array} \end{array}

Equations (145) and (148) could be then simplified:

(156)

\begin{array}{l} (a - b) \frac{d^{2} ω}{d a d b} - \frac{A}{B} . \frac{d ω}{d a} + \frac{B}{A} . \frac{d ω}{d b} = 0 \\ \frac{d^{2} x}{d a d b} = 0 \end{array}

Then Legendre deduced that three coordinates could be given by two arbitrary functions:

(157)

{\begin{array}{l} x = \frac{d ϕ}{d a} + \frac{d ψ}{d b} \\ y = ϕ - a \frac{d ϕ}{d a} + ψ - b \frac{d ψ}{d b} \\ z = - \int A \frac{d^{2} ϕ}{d a^{2}} d a + \int B \frac{d^{2} ψ}{d b^{2}} d b \end{array}

This is the integral solution of “Minimal surface” Lagrange equation (Legendre recovered the solution given by Monge in 1784).

A2. Gromov Inner Product

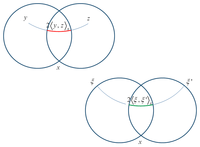
As other generalization of inner product, we can consider for specific case CAT(-1)-space[141,142] (generalization of simply connected Riemannian manifold of negative curvature lower than unity) or for an Homogeneous Symmetric Bounded domains, a “generative” Gromov Inner Product between points y–z (relatively to x) that is defined by the distance [143,144]:

(158)

{〈 y, z 〉}_{x} = \frac{1}{2} (d (x, y) + d (x, z) - d (y, z))

with d(.,.) the distance in CAT(−1). This Gromov Inner Product is illustrated in Figure 6. Intuitively, this inner product measures the distance of x to the geodesics between y to z. This Inner product could be also defined for points on the Shilov Boundary of the domain through Busemann distance:

(159)

{〈 ξ, ξ^{'} 〉}_{x} = \frac{1}{2} (B_{ξ} (x, p) + B_{ξ^{'}} (x, p))

Independent of p, where $B_{ξ} (x, y) = \underset{t \to + \infty}{L i m} [| x - r (t) | - | y - r (t) |]$ is the horospheric distance, from x to y relatively to ξ, with r(t) geodesic ray. We have the property that:

(160)

{〈 ξ, ξ^{'} 〉}_{x} = \underset{\begin{array}{l} y \to ξ \\ y^{'} \to ξ^{'} \end{array}}{L i m} {〈 y, y^{'} 〉}_{x}

We can then define a visual metric on the Shilov boundary by:

(161)

\begin{array}{l} d_{x} (ξ, ξ^{'}) = e^{- {〈 ξ, ξ^{'} 〉}_{x}} if ξ \neq ξ^{'} \\ d_{x} (ξ, ξ^{'}) = 0 otherwise \end{array}

We can then define the characteristic function according to the origin 0:

(162)

Φ (x) = - log \int_{Ω^{*}} e^{- {〈 x, γ 〉}_{0}} d γ or Φ_{Ω} (x) = - log \int_{Ω^{*}} e^{- \frac{1}{2} (d (0, x) + d (0, γ) - d (x, y))} d γ

and:

(163)

Φ^{*} (x^{*}) = {〈 x, x^{*} 〉}_{0} - Φ (x) = \frac{1}{2} (d (0, x) + d (0, x^{*}) - d (x, x^{*})) - Φ (x)

(164)

d (x, x^{*}) = (d (0, x^{*}) - 2 Φ^{*} (x^{*})) + (d (0, x) - 2 Φ (x))

with the center of gravity:

(165)

x^{*} = \int_{Ω^{*}} γ . e^{- {〈 x, γ 〉}_{0}} d γ / \int_{Ω^{*}} e^{- {〈 x, γ 〉}_{0}} d γ

All these relations are also true on the Shilov Boundary:

(166)

Φ (ξ) = - log \int_{\partial Ω^{*}} e^{- {〈 ξ, ξ^{'} 〉}_{0}} d ξ^{'} = - log \int_{\partial Ω^{*}} d_{0} (ξ, ξ^{'}) . d ξ^{'}

where $\int_{\partial Ω^{*}} d_{0} (ξ, ξ^{'}) . d ξ^{'}$ is the functional of Busemann barycenter on the Shilov Boundary ∂Ω^* (existence and unicity of this barycenter have been proved by Cartan [14] for Cartan-Hadamard Spaces).

A3. The Cohomology of a Dynamical Group

In the following, we give some details of Souriau development about the Moment of the G action (see Figure 7) and the Cohomology of a dynamical group (see Figure 8). Other details about Symplectic Geometry could be found in [145] or [146].

If G is a dynamical group of a symplectic manifold V, torsor μ is called a moment of the G-action, if there is a differential map x ↦ μ from V to ℊ^* such that:

(167)

σ (Z_{V} (x)) \equiv - d [μ . Z]

To every torsor μ, there corresponds a field [x ↦ ω̄] of 1-forms (Maurer-Cartan forms) on G which is invariant under right translation and which takes the value μ when x is the identity element:

(168)

σ_{V} = d \bar{ω}

Using the moment of the G action, Souriau has introduced the following theorem on the Cohomology of a dynamical group:

Theorem

Let V be a connected symplectic manifold and let G be a dynamical group of V possessing a moment μ. Finally, let ψ denote the map x ↦ μ from V to the space ℊ^* of torsor of G:

There exists a differential map θ:G → ℊ^*:

(169)

θ (a) \equiv ψ ({\bar{a}}_{V} (x)) - {\bar{a}}_{g^{*}} (ψ (x))

The derivative f = D(θ)(e) is a 2-form on the Lie algebra ℊ of G:

(170)

f (Z) ([Z^{'}, Z^{″}]) + f (Z^{'}) ([Z^{″}, Z]) + f (Z^{″}) ([Z, Z^{'}]) \equiv 0

Then, the following identities hold:

(171)

σ (Z_{V} (x)) (Z_{V}^{'} (x)) \equiv μ . [Z, Z^{'}] + f (Z) (Z^{'})

(172)

D (ψ) (x) (Z_{V} (x)) \equiv ψ (x) . a d (Z) + f (Z)

Conflicts of Interest

The author declares no conflict of interest.

References

Massieu, F. Sur les Fonctions caractéristiques des divers fluides. Comptes Rendus de l’Académie des Sciences 1869, 69, 858–862. (In French).
Massieu, F. Addition au précédent Mémoire sur les Fonctions caractéristiques. Comptes Rendus de l’Académie des Sciences 1869, 69, 1057–1061. (In French).
Massieu, F. Thermodynamique: Mémoire sur les Fonctions Caractéristiques des Divers Fluides et sur la Théorie des Vapeurs; Académie des Sciences: Paris, France, 1876; p. 92. (In French).
Duhem, P. Sur les équations générales de la Thermodynamique. Annales Scientifiques de l’Ecole Normale Supérieure 1891, 8, 231–266. (In French).
Duhem, P. Commentaire aux principes de la Thermodynamique—Première partie. Journal de Mathématiques pures et appliquées 1892, 8, 269–330. (In French).
Duhem, P. Commentaire aux principes de la Thermodynamique—Troisième partie. Journal de Mathématiques pures et appliquées 1894, 10, 207–286. (In French).
Duhem, P. Les théories de la chaleur. Revue des deux Mondes 1895, 130, 851–868.
Gibbs, J.W. Graphical Methods in the Thermodynamics of Fluids. In The Scientific Papers of J. Willard Gibbs; Bumstead, H.A., van Name, R.G., Eds.; Dover: New York, NY, USA, 1961.
Poincaré, H. Calcul des Probabilités; Gauthier-Villars: Paris, France, 1896. (In French).
Poincaré, H. Thermodynamique, Cours de Physique Mathématique, 1892. Available online: http://gallica.bnf.fr/ark:/12148/bpt6k2048983 (accessed on 30 July 2014). In French.
Vinberg, E.B. Structure of the Group of Automorphisms of a Homogeneous Convex Cone. Trudy Moskovskogo Matematicheskogo Obshchestva 1965, 13, 56–83.
Faraut, J.; Koranyi, A. Analysis on Symmetric Cones, Oxford Mathematical Monographs; The Clarendon Press, Oxford University Press: New York, NY, USA, 1994.
Lichnerowicz, A. Espaces homogènes Kähleriens. In Colloque de Géométrie Différentielle; Pub. du CNRSP: Paris, France, 1953; pp. 171–184. (In French).
Cartan, E. Sur les domaines bornés de l’espace de n variables complexes. Abh. Math. Seminar Hamburg 1935, 1, 116–162. (In French).
Siegel, C.L. Über der analytische Theorie der quadratischen Formen. Ann. Math 1935, 36, 527–606. (In German).
Siegel, C.L. Symplectic geometry. Amer. J. Math 1943, 65, 1–86.
Marle, C.M. On mechanical systems with a Lie group as configuration space. Jean Leray’99 Conference, Proceedings of the Karlskrona Conference in the Honor of Jean Leray, Kluwer, Dordrecht, The Netherlands, 2003; de Gosson, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 183–203.
Marle, C.M. On Henri Poincaré’s note “Sur une forme nouvelle des équations de la mécanique”. J. Geom. Symmetry Phys 2013, 29, 1–38.
Friedrich, T. Die Fisher-Information und symplektische Strukturen. Math. Nachr 1991, 153, 273–296. (In German).
Gromov, M. In a Search for a Structure, Part 1: On Entropy, Available online: http://www.ihes.fr/~gromov/PDF/structre-serch-entropy-july5-2012.pdf (accessed on 23 June 2013).
Gromov, M. Convex Sets and Kähler Manifolds. In Advances in Differential Geometry and Topology; Tricerri, F., Ed.; World Scientific: Singapore, Singapore, 1990; pp. 1–38.
Gromov, M. Entropy and Isoperimetry for Linear and non-Linear Group Actions. Groups Geom. Dyn 2008, 2, 499–593.
Gromov, M. Carnot-Carathéodory spaces seen from within. In Progress in Mathematics; Springer: Berlin/Heidelberg, Germany, 1996; Volume 144.
Ollivier, Y.; Akimoto, Y. Objective Improvement in Information-Geometric Optimization. In Foundations of Genetic Algorithms XII; Springer: Berlin/Heidelberg, Germnay, 2013.
Bensadon, J. Black-box optimization using geodesics in statistical manifolds. 2013. arXiv:1309.7168.
Bennequin, D. Dualités de champs et de cordes. Séminaire N. Bourbaki 2003, 899, 117–148. (In French).
Bennequin, D. Dualité Physique-Géométrie et Arithmétique, Avalable online: http://archive.numdam.org/ARCHIVE/SB/SB_2001-2002__44_/SB_2001-2002__44__117_0/SB_2001-2002__44__117_0.pdf (accessed on 16 June 2014).
Chasles, M. Aperçu Historique sur L’origine et le Développement des Méthodes en Géométrie; Gauthier-Villars: Paris. France 1837. (In French).
Gergonne, J.D. Polémique mathématique. Réclamation de M. le capitaine Poncelet (extraite du bulletin universel des annonces et nouvelles scientifiques); avec des notes. Annales de Mathématiques Pures et Appliquées 1827–1828, 18, 125. (In French).
Poncelet, J.V. Traité des propriétés projectives des figures; Gauthier-Villars: Paris, France, 1822. (In French).
André, Y. Dualités, Sixième séance, ENS, Séminaire MaxMux. In Leçons de Mathématiques contemporaines à l'IRCAM; ENS: Paris, France, 2009; Volume Chap. 6. (In French).
Atiyah, M.F. Duality in mathematics and physics, Available online: https://www.fme.upc.edu/arxius/butlleti-digital/riemann/071218_conferencia_atiyah-d_article.pdf (accessed on 20 June 2014).
Von Oettingen, A.J. Das duale System der Harmonie (Part 1). Annalen der Naturphilosophie 1902, 1, 62–75. (In German).
Von Oettingen, A.J. Das duale System der Harmonie (Part 2). Annalen der Naturphilosophie 1903, 2, 375–403. (In German).
Von Oettingen, A.J. Das duale System der Harmonie (Part 3). Annalen der Naturphilosophie 1904, 3, 241–269. (In German).
Von Oettingen, A.J. Das duale System der Harmonie (Part 4). Annalen der Naturphilosophie 1905, 4, 116–152. (In German).
Von Oettingen, A.J. Das duale System der Harmonie (Part 5). Annalen der Naturphilosophie 1906, 5, 449–503. (In German).
Von Oettingen, A.J. Das duale Harmoniesystem; C.F.W. Siegel’s musikalienhandlung; R. Linnemann: Leipzig, Germany, 1913. (In German).
Moreau, J.J. Fonctions convexes duales et points proximaux dans un espace hilbertien. Comptes Rendus de l’Académie des Sciences 1962, 255, 2897–2899. (In French).
Zia, R.K.P.; Redish, E.F.; McKay, S.R. Making Sense of the Legendre Transform. 2009. arXiv:0806.1147.
Koszul, J.L. Variétés localement plates et convexité. Osaka. J. Math 1965, 2, 285–290. (In French).
Koszul, J.L. Exposés sur les Espaces Homogènes Symétriques; Publicação da Sociedade de Matematica de São Paulo: São Paulo, Brazil, 1959. (In French).
Koszul, J.L. Sur la forme hermitienne canonique des espaces homogènes complexes. Can. J. Math 1955, 7, 562–576. (In French).
Koszul, J.L. Lectures on Groups of Transformations; Tata Institute of Fundamental Research: Bombay, India, 1965.
Koszul, J.L. Domaines bornées homogènes et orbites de groupes de transformations affines. Bull. Soc. Math. Fr 1961, 89, 515–533. (In French).
Koszul, J.L. Ouverts convexes homogènes des espaces affines. Math. Z 1962, 79, 254–259. (In French).
Koszul, J.L. Déformations des variétés localement plates. Ann. Inst. Fourier 1968, 18, 103–114. (In French).
Vinberg, E.B. Homogeneous convex cones. Trans. Mosc. Math. Soc 1963, 12, 340–363.
Vinberg, E.B. The Theory of Homogeneous Convex Cones. Trudy Moskovskogo Ma tematicheskogo Obshchestva 1963, 12, 303–358.
Jensen, J.L.W. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math 1906, 30, 175–193. (In French).
Needham, T. A Visual Explanation of Jensen’s Inequality. Am. Math. Mon 1993, 8, 768–777.
Jaynes, E.T. Information Theory Statistical Mechanics. Phys. Rev. Ser. II 1957, 106, 620–630.
Jaynes, E.T. Information Theory and Statistical Mechanics II. Phys. Rev. Ser 1957, 108, 171–190.
Jaynes, E.T. Prior Probabilities. IEEE Trans. Syst. Sci. Cybern 1968, 4, 227–241.
Dacunha-Castelle, D.; Gamboa, F. Maximum d’entropie et problèmes des moments. Ann. Inst. H. Poincaré Prob. Stat 1990, 26, 567–596. (In French).
Gamboa, F.; Gassiat, E. Maximum d’entropie et problème des moments: Cas multidimensionnel. Probab. Math. Stat 1991, 12, 67–83. (In French).
Dacunha-Castelle, D.; Gamboa, F. Maximum de l’entropie sous contraintes non linéaires. Ann. Inst H. Poincaré Prob. Stat 1990, 4, 567–596. (In French).
Krein, M.G.; Nudelman, A.A. The Markov Moment Problem And Extremal Problems; American Mathematical Society: New York, NY, USA, 1977.
Souriau, J.M. Définition covariante des équ ilibres thermodynamiques. Suppl. Nuov. Cimento 1966, 1, 203–216. (In French).
Crouzeix, J.P. A Relationship Between The Second Derivatives of a Convex Function and of Its Conjugate. Math. Program 1977, 3, 364–365.
Seeger, A. Second Derivative of a Convex Function and of Its Legendre-Fenchel Transformate. SIAM J. Optim 1992, 2, 405–424.
Hiriart-Urruty, J.B. A new set-valued second-order derivative for convex functions. In Mathematics for Optimization; Mathematical Studies Series 129; Elsevier: Amsterdam, The Netherlands, 1986.
Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc 1945, 37, 81–89.
Fréchet, M. Sur l’extension de certaines évaluations statistiques au cas de petits échantillons. Revue de l’Institut International de Statistique 1943, 11, 182–205. (In French).
Koszul, J.L. Trajectoires Convexes de Groupes Affines Unimodulaires. In Essays on Topology and Related Topics; Springer: Berlin, Germany, 1970; pp. 105–110.
Vey, J. Sur les Automorphismes Affines des Ouverts Convexes Saillants. Annali della Scuola Normale Superiore di Pisa, Classe di Science 1970, 24, 641–665. (In French).
Vey, J. Sur une notion d’hyperbolicité des variables localement plates. In Thèse de Troisième Cycle de Mathématiques Pures; Faculté des sciences de l’université de Grenoble: Grenoble, France, 1969. (In French).
Shima, H. Geometry of Hessian Structures. In Springer Lecture Notes in Computer Science; Nielsen, F., Frederic, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8085, pp. 37–55.
Shima, H. The Geometry of Hessian Structures; World Scientific: Singapore, Singapore, 2007.
Byande, P.M.; Ngakeu, F.; Nguiffo Boyom, M.; Wolak, R. KV-Cohomology and Differential Geometry of Affinely Flat Manifolds. Information Geometry. Afr. Diaspora J. Math 2012, 14, 197–226.
Sasaki, T. A Note on Characteristic Functions and Projectively Invariant Metrics on a Bounded Convex Domain. Tokyo J. Math 1985, 8, 49–79.
Sasaki, T. Hyperbolic Affine Hyperspheres. Nagoya Math. J 1980, 77, 107–123.
Rothaus, O.S. The Construction of Homogeneous Convex Cones. Ann. Math 1966, 83, 358–376.
Barbaresco, F. Information Geometry of Covariance Matrix: Cartan-Siegel Homogeneous Bounded Domains, Mostow/Berger Fibration and Fréchet Median, Matrix Information Geometry; Bhatia, R., Nielsen, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 199–256.
Arnaudon, M.; Barbaresco, F.; Yang, L. Riemannian medians and means with applications to radar signal processing. IEEE J. Sel. Top. Signal Process 2013, 7, 595–604.
Yang, L. Médianes de Mesures de Probabilité dans les Variétés Riemanniennes et Applications à la Détection de Cibles Radar. Thales Ph.D, Thèse de l’Université de Poitiers, Poitiers, France, 2012. (In French).
Barbaresco, F. Information/Contact Geometries and Koszul Entropy, Geometric Science of Information. In Lecture Notes in Computer Science; Nielsen, F., Barbaresco, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8085, pp. 604–611.
Cartan, E. Le rôle de la Théorie des Groupes de Lie Dans L’évolution de la Géométrie Moderne; International Mathematical Union: Berlin, Germany, 1936. (In French).
Souriau, J.M. Thermodynamique et géométrie. In Differential Geometrical Methods in Mathematical Physics II; Bleuler, K., Reetz, A., Petry, H.R., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 369–397.
Souriau, J.M. Géométrie de l’espace de phases. Comm. Math. Phys 1966, 374, 1–30. (In French).
Souriau, J.M. On Geometric Mechanics. Discret. Cont. Dyn. Syst. J 2007, 19, 595–607.
Souriau, J.M. Structure des systèmes dynamiques; Editions Jacques Gabay: Paris, France, 1970. (In French).
Souriau, J.M. Structure of Dynamical Systems, volume 149 of Progress in Mathematics. In A Symplectic View of Physics; Birkhäuser Boston Inc.: Boston, MA, USA, 1997.
Souriau, J.M. Thermodynamique Relativiste des Fluides; Centre de Physique Théorique: Marseille, France, 1977. (In French).
Souriau, J.M.; Iglesias, P. Heat Cold and Geometry. Differential Geometry and Mathematical Physics, Mathematical Physics Studies Volume; Springer: Amsterdam, The Netherlands, 1983; pp. 37–68.
Souriau, J.M. Dynamic Systems Structure (chap.16 convexité, chap. 17 Mesures, chap. 18 Etats statistiques, Chap. 19 Thermodynamique), available in Souriau archive (document sent by C. Vallée), unpublished technical notes. 1980.
Souriau, J.M. Géométrie Symplectique et Physique Mathématique; Éditions du C.N.R.S.: Paris, France, 1975. (In French).
Ruelle, D. Statistical Mechanics. Rigorous Results; Imperial College Press: London, UK, 1999.
Ruelle, D. Hasard et Chaos; Editions Odile Jacob: Paris, France, 1991.
Ruelle, D. Thermodynamic Formalism: The Mathematical Structure of Equilibrium Statistical Mechanics, 2nd ed. ed.; Cambridge Mathematical Library; Cambridge University Press: Cambridge, UK, 2004.
Vallée, C. Lois de Comportement des Milieux Continus Dissipatifs Compatibles Avec la Physique Relativiste. Ph.D Thesis, Poitiers University, Poitiers, France, 1987. (In French).
Vallée, C. Relativistic thermodynamics of continua. Int. J. Eng. Sci 1981, 19, 589–601.
De Saxcé, G.; Vallée, C. Bargmann group, momentum tensor and Galilean invariance of Clausius-Duhem inequality. Int. J. Eng. Sci 2012, 50, 216–232.
Vallée, C.; Hjiaj, M.; Fortuné, D.; de Saxcé, G. Canonical and Anti-Canonical Transformations Preserving Convexity of Potentials. J. Elast 2011, 103, 247–267.
Iglésias, P. Equilibre statistiques et géométrie symplectique en relativité générale. Annales de l'institut Henri Poincaré (A) Physique théorique 1982, 36, 257–270. (In French).
Iglésias, P. Essai de thermodynamique rationnelle des milieux continus. Annales de l'institut Henri Poincaré (A) Physique théorique 1981, 34, 1–24. (In French).
Dubois, F. Conservation Laws Invariants for Galileo Group; Cemracs Preliminary Results, Available online: http://hal.archives-ouvertes.fr/docs/00/55/53/13/PDF/dubois-cemracs99.janv2011.pdf (accessed on 20 June 2014).
Roblin, T. Ergodicité et équidistribution en courbure négative. Mémoire de la Société Mathématique de France 2003, 95, 96. (In French).
Paulin, F.; Pollicott, M.; Schapira, B. Equilibrium states in negative curvature. 2013. arXiv:1211.6242.
Coudène, Y. Gibbs measures on negatively curved manifolds. J. Dynam. Control Syst 2003, 9, 89–101.
Coudène, Y.; Schapira, B. Generic measures for geodesic flows on nonpositively curved manifolds. Dyn. Syst 2014. submitted.
Haydn, N.T.A.; Ruelle, D. Equivalence of Gibbs and equilibrium states for homeomorphisms satisfying expansiveness and specification. Comm. Math. Phys 1992, 148, 155–167.
Mohsen, O. Le bas du spectre d’une variété hyperbolique est un point selle. Ann. Sci. École Norm. Sup 2007, 40, 191–207. (In French).
Donaldson, S.K. Scalar Curvature Stability of Toric Variety. J. Differ. Geom 2002, 62, 289–349.
Abreu, M. Kähler geometry of toric varieties and extremal metrics. Int. J. Math 1998, 9, 641–651.
Guan, D. On modified Mabuchi functional and Mabuchi moduli space of kahler metrics on toric bundles. Math. Res. Lett 1999, 6, 547–555.
Guillemin, V. Kaehler structures on toric varieties. J. Differ. Geom 1994, 40, 285–309.
Guillemin, V. Moment Maps and Combinatorial Invariants of Hamiltonian Tn-Spaces; Birkhau-ser: Basel, Switzerland, 1994.
Atiyah, M.; Bott, R. The moment map and equivariant cohomology. Topology 1984, 23, 1–28.
Bruguières, A. Propriétés de convexité de l’application moment. Séminaire Bourbaki 1985, 28, 63–87. (In French).
Condevaux, M.; Dazord, P.; Molino, P. Géométrie du moment. Dans Travaux du séminaire Sud Rhodanien de Géométrie; University Lyon: Lyon, France, 1988; pp. 131–160.
Delzant, T. Hamiltoniens périodiques et images convexes de l’application moment. Bull. Soc. Math. Fr 1988, 116, 315–339. (In French).
Guillemin, V.; Sternberg, S. Convexity properties of the moment mapping. Inv. Math 1982, 67, 491–513.
Kirwan, F. Convexity properties of the moment mapping. Inv.Math 1984, 77, 547–552.
Kapranov, M. Thermodynamics and the moment map. 2011. arXiv:1108.3472v1.
Biquard, O. Métriques Kählériennes Extrémales sur les Surfaces Toriques; Société Mathématique de France: Paris, France, 2011; p. 1018. (In French).
Pavlov, V.P.; Sergeev, V.M. Thermodynamics from the Differential Geometry Standpoint. Theor. Math. Phys 2008, 157, 1484–1490.
Kozlov, V.V. Heat Equilibrium by Gibbs and Poincaré. Dokl. Ross. Akad. Nauk 2002, 382, 602–606. (In French).
Berezin, F.A. Lectures on Statistical Physics; World Scientific: Singapore, Singapore, 2007.
Poincaré, H. Réflexions sur la théorie cinétique des gaz. J. Phys. Theor. Appl 1906, 5, 369–403.
Carathéodory, C. Untersuchungen über die Grundlagen der Thermodynamik. Math. Ann 1909, 67, 355–386. (In German).
Souriau, J.M. Mécanique Classique et Géométrie Symplectique. In Report ref. CPT-84/PE-1695; CNRS Centre de Physique Théorique: Marseille, France, 1984. (In French).
Viterbo, C. Generating Functions, Symplectic Geometry and Applications. Proc. Intern. Congr. Math., Zurich 1994, 1, 537–547.
Viterbo, C. Symplectic topology as the geometry of generating functions. Math. Ann 1992, 292, 685–710.
Hörmander, L. Fourier integral operators I. Acta Math 1971, 127, 79–183.
Théret, D. A complete proof of Viterbo’s uniqueness theorem on generating functions. Topol. Appl 1999, 96, 249–266.
Chentsov, N.N. Statistical Decision Rules and Optimal Inferences (Transactions of Mathematics Monograph); American Mathematical Society: Providence, RI, USA, 1982; Volume 53.
Villani, C. (Ir)rréversibilité et entropie/(Ir)reversibility and entropy. In Séminaire Poincaré Le temps; École Polytechnique: Paris, France, 2010. (In French).
Ollivier, Y. Aspects de l’entropie en mathématiques et en physique, Available online: http://www.yann-ollivier.org/entropie/entropie.pdf (accessed on 1 January 2014). (In French).
Avantaggiati, A.; Loreti, P. On Fourier Transform, Parseval Equality, and the Inversion Formula in Idempotent Analysis. Proceedings of the 2013 European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013.
Litvinov, G.L. The Maslov Dequantization, Idempotent and Tropical Mathematics: A brief Introduction. J. Math. Sci 2007, 140, 426–444.
Leray, J. Un prolongement de la transformation de Laplace qui transforme la solution unitaire d’un opérateur hyperbolique en sa solution élémentaire. (Problème de Cauchy. IV.). Bull. Soc. Math. Fr 1962, 90, 39–156. (In French).
Leray, J. Le calcul différentiel et intégral sur une variété analytique complexe Problème de Cauchy, III. Bull. Soc. Math. Fr 1959, 82, 6–180. (In French).
Maslov, V.P. Operational Methods; MIR: Moscow, Russia, 1976.
Del Moral, P.; Doisy, M. Maslov idempotent probability calculus, I, II. Theory Probab. Appl 2000, 44, 319–332.
Del Moral, P.; Doisy, M. On the applications of Maslov optimization theory. Math. Notes 2001, 69, 232–244.
Laplace, P.S. Mémoire sur la probabilité des causes sur les évènements. In Mémoires de Mathématique et de Physique; De l’Imprimerie Royale: Paris, France, 1774. (In French).
Legendre, A.M. Mémoire Sur L’intégration de Quelques Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1787; pp. 309–351. (In French).
Monge, G. Sur le Calcul Intégral des Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1784; pp. 118–192. (In French).
Darboux, G. Leçons sur la Théorie Générale des Surfaces et les Applications Géométriques du Calcul Infinitésimal: Premiere Partie (Généralités, Coordonnées Curvilignes, Surface Minima); Gauthier-Villars: Paris, France, 1887. (In French).
Hadamard, J. Les surfaces à courbures opposées et leurs lignes géodésiques. Journal de Mathématiques Pures et Appliquées 1898, 4, 27–74. (In French).
Vesentini, E. Geometry of Homogeneous Bounded Domains; Springer-Verlag: Berlin/Heidelberg, Germany, 2011.
Bourdon, M. Structure conforme au bord et flot géodésique d’un CAT(−1)-espace. L’Enseignement Mathématique 1995, 41, 63–102. (In French).
Deza, E.; Deza, M.M. Dictionary of Distances; Elsevier: Amsterdam, The Netherlands, 2006.
Cartan, E. Leçons sur les Invariants Intégraux; Hermann: Paris, France, 1922. (In French).
Libermann, P.; Marle, C.M. Symplectic Geometry and Analytical Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987.

Figure 1. Text of Poincaré Lecture on Thermodynamic with development of the concept of “Massieu Characteristic Function”.

Click here to enlarge figure

Figure 1. Text of Poincaré Lecture on Thermodynamic with development of the concept of “Massieu Characteristic Function”.

Figure 2. (a) Pascal’s theorem, (b) Brianchon’s theorem.

Click here to enlarge figure

Figure 2. (a) Pascal’s theorem, (b) Brianchon’s theorem.

Figure 3. Legendre Transform G(y) of F(x).

Click here to enlarge figure

Figure 3. Legendre Transform G(y) of F(x).

Figure 4. Souriau figure on Lie Groups Thermodynamics.

Click here to enlarge figure

Figure 4. Souriau figure on Lie Groups Thermodynamics.

Figure 5. Generation of Koszul elements from Cartan Inner Product.

Click here to enlarge figure

Figure 5. Generation of Koszul elements from Cartan Inner Product.

Figure 6. Gromov Inner product in homogeneous bounded domains and its Shilov boundary.

Click here to enlarge figure

Figure 6. Gromov Inner product in homogeneous bounded domains and its Shilov boundary.

Figure 7. Moment of the G action.

Click here to enlarge figure

Figure 7. Moment of the G action.

Figure 8. The Cohomology of a dynamical group.

Click here to enlarge figure

Figure 8. The Cohomology of a dynamical group.

Table 1. Synthesis of Koszul and Souriau models.

Click here to display table

**Table 1.** Synthesis of Koszul and Souriau models.
	Koszul Information Geometry Model	Souriau Lie Groups Thermodynamics Model
Characteristic function	$Φ (x) = - log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ \forall x \in Ω$	$Φ (β) = - log \int_{M} e^{- β . U (ξ)} d ω \forall β \in g$

Entropy	$Φ^{} (x^{}) = - \int_{Ω^{*}} p_{x} (ξ) log p_{x} (ξ) d ξ$	$s = - \int_{M} p (ξ) log p (ξ) d ω$

Legendre Transform	Φ^(x^) = 〈x,x^*〉 − Φ(x)	s(Q) = β.Q − Φ(β)

Density of probability	p_x(ξ) = e^−〈^x^,^ξ^{〉 +} ^Φ(x)	p_β(ξ) = e⁻^β^.^U⁽^ξ^{) + Φ(}^β⁾
	$p_{x} (ξ) = \frac{e^{- 〈 ξ, x 〉}}{\int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ}$	$p_{β} (ξ) = \frac{e^{- β . U (ξ)}}{\int_{M} e^{- β . U (ξ)} d ω}$

Dual Coordinate Systems	x ∈ Ω and x^* ∈ Ω^*	β ∈ ℊ and Q ∈ ℊ^*
	$x^{} = \int_{Ω^{}} ξ . p_{x} (ξ) d ξ = \frac{\int_{Ω^{}} ξ . e^{- 〈 ξ, x 〉} d ξ}{\int_{Ω^{}} e^{- 〈 ξ, x 〉} d ξ}$	$Q = \int_{M} U (ξ) . p_{β} (ξ) d ω = \frac{\int_{M} U (ξ) e^{- β . U (ξ)} d ω}{\int_{M} e^{- β . U (ξ)} d ω}$ β Souriau Geometric Temperature U: Souriau Moment map Q: Mean of Souriau Moment Map or Geometric heat
	$x^{} = \frac{\partial Φ (x)}{\partial x}$ and $x = \frac{\partial Φ^{} (x^{})}{\partial x^{}}$	$Q = \frac{\partial Φ}{\partial β}$ and $β = \frac{\partial s}{\partial Q}$

Hessian Metric	ds² = −d²Φ(x)	ds² = −d²Φ(β)

Fisher metric	$I (x) = - E_{ξ} [\frac{\partial^{2} log p_{x} (ξ)}{\partial x^{2}}]$	$I (β) = - E_{ξ} [\frac{\partial^{2} log p_{β} (ξ)}{\partial β^{2}}]$
	$I (x) = = - \frac{\partial^{2} Φ (x)}{\partial x^{2}} = \frac{\partial^{2} log \int_{Ω^{*}} e^{- 〈 ξ, x 〉} d ξ}{\partial x^{2}}$	$I (β) = - \frac{\partial^{2} Φ (β)}{\partial β^{2}} = \frac{\partial^{2} log \int_{M} e^{- β . U (ξ)} d ω}{\partial β^{2}}$
		$I (β) = - \frac{\partial^{2} Φ (β)}{\partial β^{2}} = - \frac{\partial Q}{\partial β}$
		$K = - \frac{\partial Q}{\partial β}$ :Souriau Geometric Capacity

Table 2. Comparison of invariances for the Koszul and Souriau models.

Click here to display table

**Table 2.** Comparison of invariances for the Koszul and Souriau models.
	Koszul Information Geometry Model	Souriau Lie Groups Thermodynamics Model
Convex Cone	x∈Ω Ω convex cone	β ∈ Ω Ω convex cone: largest open subset of ℊ, Lie algebra of G, such that $\int_{M} e^{- β . U (ξ)} d ω$ and $\int_{M} ξ . e^{- β . U (ξ)} d ω$ are convergent integrals
Transformation	x→gx with g∈Aut (Ω)	β→ ā_ℊ (β)
Transformation of Potential (non invariant)	Φ_Ω(x) → Φ_Ω(gx) = Φ_Ω (x) + log(\|det g\|)	Φ (β) → Φ(ā_ℊ(β)) = Φ (β) − θ(a⁻¹)β
Transformation of Entropy (invariant)	$Φ_{Ω^{}}^{} (x^{}) \to Φ_{Ω^{}}^{} (\frac{\partial Φ_{Ω} (g x)}{\partial x}) = Φ_{Ω^{}}^{} (x^{})$ with $x^{*} = \frac{\partial Φ_{Ω} (x)}{\partial x}$	s(Q) → s′(Q′) = β′.Q′−Φ′ = β.Q − Φ = s(Q).with β′ = ā_ℊ (β) $Q^{'} = \frac{\partial Φ^{'}}{\partial β^{'}} = \frac{\partial (Φ + θ (a) {\bar{a}}_{g} (β))}{\partial {\bar{a}}_{g} (β)} = {\bar{a}}_{g^{*}} (Q) + θ (a)$ Φ′ = Φ(β′) = Φ(ā_ℊ(β)) = Φ(β) − θ(a⁻¹)β
Information Geometry Metric (invariant)	$\begin{array}{l} I (g x) = - \frac{\partial^{2} [Φ_{Ω} (x) + log (\| det g \|)]}{\partial x^{2}} \\ I (g x) = - \frac{\partial^{2} Φ_{Ω} (x)}{\partial x^{2}} = I (x) \end{array}$	$I ({\bar{a}}_{g} (β)) = - \frac{\partial^{2} [Φ (β) - θ (a^{- 1}) β]}{\partial β^{2}} = - \frac{\partial^{2} Φ (β)}{\partial β^{2}} = I (β)$

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).