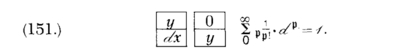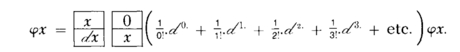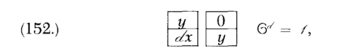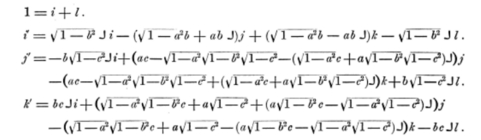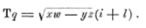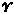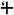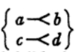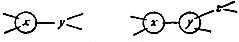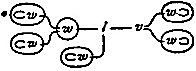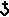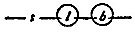Paper 3: Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Coneptions of Boole's Calculus of Logic Memoirs of the American Academy, vol. 9, pp. 317-78 (1870). Reprinted separately by Welch, Bigelow and Company, Cambridge, Mass., 1870, pp. 1-62. "In 1870 I made a contribution to this subject [logic] which nobody who masters the subject can deny was the most important excepting Boole's original work that ever has been made." — From the "Lowell Lectures," 1903. †1
§1. De Morgan's NotationE
45. Relative terms usually receive some slight treatment in works upon logic, but the only considerable investigation into the formal laws which govern them is contained in a valuable paper by Mr. De Morgan in the tenth volume of the Cambridge Philosophical Transactions. "On the Syllogism No. IV, and on the Logic of Relations," pp. 331-58, dated 1859.†2 He there uses a convenient algebraic notation, which is formed by adding to the well-known spiculæ of that writer the signs used in the following examples.
X . . LY signifies that X is some one of the objects of thought which stand to Y in the relation L, or is one of the L's of Y.
X . LMY signifies that X is not an L of an M of Y.
X . . (L,M)Y signifies that X is either an L or an M of Y.
LM' an L of every M. L[,]M an L of none but M's.
L[-1]Y something to which Y is L. l (small L) non-L.
This system still leaves something to be desired. Moreover, Boole's logical algebra has such singular beauty, so far as it goes, that it is interesting to inquire whether it cannot be extended over the whole realm of formal logic, instead of being restricted to that simplest and least useful part of the subject, the logic of absolute terms, which, when he wrote, was the only formal logic known. The object of this paper is to show that an affirmative answer can be given to this question. I think there can be no doubt that a calculus, or art of drawing inferences, based upon the notation I am to describe, would be perfectly possible and even practically useful in some difficult cases, and particularly in the investigation of logic. I regret that I am not in a situation to be able to perform this labor, but the account here given of the notation itself will afford the ground of a judgment concerning its probable utility.
46. In extending the use of old symbols to new subjects, we must of course be guided by certain principles of analogy, which, when formulated, become new and wider definitions of these symbols. As we are to employ the usual algebraic signs as far as possible, it is proper to begin by laying down definitions of the various algebraic relations and operations. The following will, perhaps, not be objected to.
§2. General Definitions of the Algebraic Signs
47. Inclusion in or being as small as is a transitive relation. The consequence holds that I use the sign ⤙ in place of ≦. My reasons for not liking the latter sign are that it cannot be written rapidly enough, and that it seems to represent the relation it expresses as being compounded of two others which in reality are complications of this. It is universally admitted that a higher conception is logically more simple than a lower one under it. Whence it follows from the relations of extension and comprehension, that in any state of information a broader concept is more simple than a narrower one included under it. Now all equality is inclusion in, but the converse is not true; hence inclusion in is a wider concept than equality, and therefore logically a simpler one. On the same principle, inclusion is also simpler than being less than. The sign ≦ seems to involve a definition by enumeration; and such a definition offends against the laws of definition.†P1
| If |
x ⤙ y, |
| and |
y ⤙ z, |
| then |
x ⤙ z. |
48. Equality is the conjunction of being as small as and its converse. To say that x = y is to say that x ⤙ y and y ⤙ x.
49. Being less than is being as small as with the exclusion of its converse. To say that x < y is to say that x ⤙ y, and that it is not true that y ⤙ x.
50. Being greater than is the converse of being less than. To say that x > y is to say that y < x.
51. Addition is an associative operation. That is to say, I write a comma below the sign of addition, except when (as is the case in ordinary algebra) the corresponding inverse operation (subtraction) is determinative, [i.e., except when the addition is arithmetical.] †P1
(x  y) y)  z = x z = x  (y (y  z). z).
Addition is a commutative operation. That is,
x  y = y y = y  x. x.
52. Invertible I.e., arithmetical. †1 addition is addition the corresponding inverse of which is determinative. The last two formulæ hold good for it, and also the consequence that
| If |
x + y = z, |
| and |
x + y' = z, |
| then |
y = y'. See 27. †2 |
53. Multiplication is an operation which is doubly distributive with reference to addition. That is,
x(y  z) = xy z) = xy  xz, xz,
(x  y)z = xz y)z = xz  yz. yz.
Multiplication is almost invariably an associative operation. Cf. 55, 69f. †3
(xy)z = x(yz).
Multiplication is not generally commutative. If we write commutative I.e., "non-relative," or what was before called "logical." †4 multiplication with a comma, Cf. 73, 74n. †5 we have
x,y = y,x.
54. Invertible I.e., arithmetical. See 75. †1 multiplication is multiplication whose corresponding inverse operation (division) is determinative. We may indicate this by a dot; The symbolism of the earlier papers is here slightly modified: the simple conjunction of terms now represents relative, instead of arithmetical, multiplication, and the dot is introduced to represent arithmetical multiplication. The comma, however, is still retained for logical multiplication. †2 and then the consequence holds that
| If |
x.y = z, |
| and |
x.y'= z, |
| then |
y = y'. See 36. †3 |
55. Functional multiplication Cf. 71 and 72.†4 is the application of an operation to a function. It may be written like ordinary multiplication; but then there will generally be certain points where the associative principle does not hold. Thus, if we write (sin abc) def, there is one such point. If we write (log (base abc) def) ghi, there are two such points. The number of such points depends on the nature of the symbol of operation, and is necessarily finite. If there were many such points, in any case, it would be necessary to adopt a different mode of writing such functions from that now usually employed. We might, for example, give to "log" such a meaning that what followed it up to a certain point indicated by a † should denote the base of the system, what followed that to the point indicated by a ‡ should be the function operated on, and what followed that should be beyond the influence of the sign "log." Thus log abc † def ‡ ghi would be (log abc) ghi, the base being def. In this paper I shall adopt a notation very similar to this, which will be more conveniently described further on.
56. The operation of involution obeys the formula In the notation of quaternions Hamilton has assumed (xy)z=x(zy)instead of(xy)z=x(yz), although it appears to make but little difference which he takes. Perhaps we should assume two involutions, so that (xy)z=x(yz),z(yx)=(zy)x. But in this paper only the former of these is required. [See 113ff. for the latter.] †P1
(xy)z = x(yz).
Involution, also, follows the indexical principle.
xy  z = xy,xz. z = xy,xz.
Involution, also, satisfies the binomial theorem. See 77. †1
(x  y)z = xz y)z = xz  Σpxz-p,yp Σpxz-p,yp  yz, yz,
where Σp denotes that p is to have every value less than z, and is to be taken out of z in all possible ways, and that the sum of all the terms so obtained of the form xz-p,yp is to be taken.
57. Subtraction is the operation inverse to addition. We may write indeterminative I.e., logical; see 10. †2 subtraction with a comma below the usual sign. Then we shall have that
(x  y) y)  y = x, y = x,
(x - y) + y = x,
(x + y) - y = x.
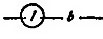
58. Division is the operation inverse to multiplication. Since multiplication is not generally commutative it is necessary to have two signs for division. I shall take
(x:y)y = x,
x y/x = y.
59. Division inverse to that multiplication which is indicated by a comma may be indicated by a semicolon. So that
(x;y),y = x. See 10 (24). †3
60. Evolution and taking the logarithm are the operations inverse to involution.
(x√y)x = y,
xlogxy = y.
61. These conditions are to be regarded as imperative. But in addition to them there are certain other characters which it is highly desirable that relations and operations should possess, if the ordinary signs of algebra are to be applied to them. These I will here endeavour to enumerate.
1. It is an additional motive for using a mathematical sign to signify a certain operation or relation that the general conception of this operation or relation should resemble that of the operation or relation usually signified by the same sign. In particular, it will be well that the relation expressed by ⤙ should involve the conception of one member being in the other; addition, that of taking together; multiplication, that of one factor's being taken relatively to the other (as we write 3 X 2 for a triplet of pairs, and Dφ for the derivative of φ); and involution, that of the base being taken for every unit of the exponent.
2. In the second place, it is desirable that, in certain general circumstances, determinate numbers should be capable of being substituted for the letters operated upon, and that when so substituted the equations should hold good when interpreted in accordance with the ordinary definitions of the signs, so that arithmetical algebra should be included under the notation employed as a special case of it. For this end, there ought to be a number known or unknown, which is appropriately substituted in certain cases, for each one of, at least, some class of letters.
3. In the third place, it is almost essential to the applicability of the signs for addition and multiplication, that a zero and a unity should be possible. By a zero I mean a term such that
x  0 = x, 0 = x,
whatever the signification of x; and by a unity a term for which the corresponding general formula
x1 = x
holds good. On the other hand, there ought to be no term a such that ax=x, independently of the value of x.
4. It will also be a strong motive for the adoption of an algebraic notation, if other formulæ which hold good in arithmetic, such as
xz,yz = (x,y)z,
1x = x,
x1 = x,
x0 = 0,
continue to hold good; if, for instance, the conception of a differential is possible, and Taylor's Theorem holds, and  The symbol represents the base of Naperian logarithms, the symbol represents π and represents the square root of the negative in Benjamin Peirce's Linear Associative Algebras, §15ff (1870). †1 or (1+i)1/i plays an important part in the system, if there should be a term having the properties of The symbol represents the base of Naperian logarithms, the symbol represents π and represents the square root of the negative in Benjamin Peirce's Linear Associative Algebras, §15ff (1870). †1 or (1+i)1/i plays an important part in the system, if there should be a term having the properties of  The symbol represents the base of Naperian logarithms, the symbol represents π and represents the square root of the negative in Benjamin Peirce's Linear Associative Algebras, §15ff (1870). †1 (3.14159), or properties similar to those of space should otherwise be brought out by the notation, or if there should be an absurd expression having the properties and uses of The symbol represents the base of Naperian logarithms, the symbol represents π and represents the square root of the negative in Benjamin Peirce's Linear Associative Algebras, §15ff (1870). †1 (3.14159), or properties similar to those of space should otherwise be brought out by the notation, or if there should be an absurd expression having the properties and uses of  The symbol represents the base of Naperian logarithms, the symbol represents π and represents the square root of the negative in Benjamin Peirce's Linear Associative Algebras, §15ff (1870). †1 or the square root of the negative. The symbol represents the base of Naperian logarithms, the symbol represents π and represents the square root of the negative in Benjamin Peirce's Linear Associative Algebras, §15ff (1870). †1 or the square root of the negative.
§3. Application of the Algebraic Signs to Logic
62. While holding ourselves free to use the signs of algebra in any sense conformable to the above absolute conditions, we shall find it convenient to restrict ourselves to one particular interpretation except where another is indicated. I proceed to describe the special notation which is adopted in this paper.
Use of the Letters
63. The letters of the alphabet will denote logical signs. Now logical terms are of three grand classes. The first embraces those whose logical form involves only the conception of quality, and which therefore represent a thing simply as "a —." These discriminate objects in the most rudimentary way, which does not involve any consciousness of discrimination. They regard an object as it is in itself as such (quale); for example, as horse, tree, or man. These are absolute terms. The second class embraces terms whose logical form involves the conception of relation, and which require the addition of another term to complete the denotation. These discriminate objects with a distinct consciousness of discrimination. They regard an object as over against another, that is as relative; as father of, lover of, or servant of. These are simple relative terms. The third class embraces terms whose logical form involves the conception of bringing things into relation, and which require the addition of more than one term to complete the denotation. They discriminate not only with consciousness of discrimination, but with consciousness of its origin. They regard an object as medium or third between two others, that is as conjugative; as giver of — to —, or buyer of — for — from —. These may be termed conjugative terms. The conjugative term involves the conception of third, the relative that of second or other, the absolute term simply considers an object. Cf. the discussion on the categories in vol. 1, bk. III, and on signs in vol. 2, bk. II. †1 No fourth class of terms exists involving the conception of fourth, because when that of third is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. Cf. 421 and 1.347. †2 Whether this reason for the fact that there is no fourth class of terms fundamentally different from the third is satisfactory or not, the fact itself is made perfectly evident by the study of the logic of relatives. I shall denote absolute terms by the Roman alphabet, a, b, c, d, etc.; relative terms by italics, a, b, c, d, etc.; and conjugative terms by a kind of type called Kennerly, 𝐚, 𝐛, 𝐜, 𝐝, etc.
I shall commonly denote individuals by capitals, and generals Cf. 69n. †3 by small letters. General symbols for numbers will be printed in black-letter, thus, 𝖆, 𝖇, 𝖈, 𝖉, etc. The Greek letters will denote operations.
64. To avoid repetitions, I give here a catalogue of the letters I shall use in examples in this paper, with the significations I attach to them.
| a. animal. |
p. President of the United States Senate. |
| b. black. |
r. rich person. |
| f. Frenchman. |
u. violinist. |
| h. horse. |
v. Vice-President of the United States. |
| m. man. |
w. woman. |
| a. enemy. |
h. husband. o. owner. |
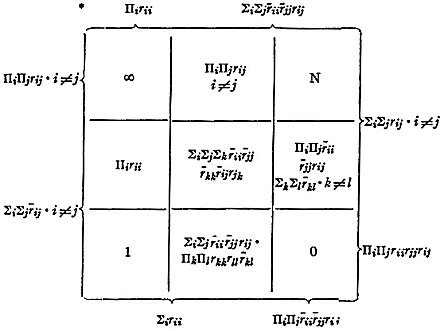
| b. benefactor. |
l. lover. s. servant. |
| c. conqueror. |
m. mother. w. wife. |
| e. emperor. |
n. not. |
| 𝗴. giver to—of—. |
𝐛. betrayer to—of—. |
| 𝘄. winner over of—to—from—. |
𝘁. transferrer from—to—. |
Numbers Corresponding to Letters
65. I propose to use the term "universe" to denote that class of individuals about which alone the whole discourse is understood to run. The universe, therefore, in this sense, as in Mr. De Morgan's, "On the Structure of the Syllogism," Section 1, Cambridge Philosophical Transactions, vol. 8 (1846); Formal Logic, p. 37 (1847). †1 is different on different occasions. In this sense, moreover, discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains. Cf. 2.518ff. †2
I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (men), the number of "tooth of" would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus [t].
The Signs of Inclusion, Equality, etc.
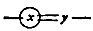
66. I shall follow Boole Laws of Thought, p. 27.†3 in taking the sign of equality to signify identity. Thus, if v denotes the Vice-President of the United States, and p the President of the Senate of the United States,
v = p
means that every Vice-President of the United States is President of the Senate, and every President of the United States Senate is Vice-President. The sign "less than" is to be so taken that
f < m
means every Frenchman is a man, but there are men besides Frenchmen. Drobisch has used this sign in the same sense. According to De Morgan, Formal Logic, p. 334. De Morgan refers to the first edition of Drobisch's Logic. The third edition contains nothing of the sort. †P1 It will follow from these significations of = and < that the sign ⤙ (or ≦, "as small as") will mean "is." Thus,
f ⤙ m
means "every Frenchman is a man," without saying whether there are any other men or not. So,
m ⤙ l
will mean that every mother of anything is a lover of the same thing; although this interpretation in some degree anticipates a convention to be made further on. These significations of = and < plainly conform to the indispensable conditions. Upon the transitive character of these relations the syllogism depends, for by virtue of it, from
|
f ⤙ m |
| and |
m ⤙ a, |
| we can infer that |
f ⤙ a; |
that is, from every Frenchman being a man and every man being an animal, that every Frenchman is an animal. But not only do the significations of = and < here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. Cf. 42-44. A class is the extension of a collection; see e.g., 537n. †1 So, to write 5 < 7 is to say that 5 is part of 7, just as to write f < m is to say that Frenchmen are part of men. Indeed, if f < m, then the number of Frenchmen is less than the number of men, and if v = p, then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.
The Signs for Addition
67. The sign of addition is taken by Boole, Op. cit., p. 33. †2 so that
x + y
denotes everything denoted by x, and, besides, everything denoted by y. Thus
m + w
denotes all men, and, besides, all women. This signification for this sign is needed for connecting the notation of logic with that of the theory of probabilities. But if there is anything which is denoted by both the terms of the sum, the latter no longer stands for any logical term on account of its implying that the objects denoted by one term are to be taken besides the objects denoted by the other. For example,
f + u
means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are besides themselves. For this reason alone, in a paper which is published in the Proceedings of the Academy for March 17, 1867, In 3. †1 I preferred to take as the regular addition of logic a noninvertible process, such that
m  b b
stands for all men and black things, without any implication that the black things are to be taken besides the men; and the study of the logic of relatives has supplied me with other weighty reasons for the same determination. Since the publication of that paper, I have found that Mr. W. Stanley Jevons, in a tract called Pure Logic, or the Logic of Quality, [1864] Ch. 6, §63; ch. 15, §177ff.†2 had anticipated me in substituting the same operation for Boole's addition, although he rejects Boole's operation entirely and writes the new one with a + sign while withholding from it the name of addition. In another book [Substitution of Similars (1869) and subsequent works] he uses the sign ·|· instead of +. †P1 It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions. But the notation has other recommendations. The conception of taking together involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five. Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves—provided all the terms summed are mutually exclusive. Addition being taken in this sense, nothing is to be denoted by zero, for then
x  0 = x, 0 = x,
whatever is denoted by x; and this is the definition of zero. Cf. 82. †1 This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of zero and that of nothing, and because we shall thus have
[0] = 0
The Signs for Multiplication
68. I shall adopt for the conception of multiplication the application of a relation, in such a way that, for example, lw shall denote whatever is lover of a woman. This notation is the same as that used by Mr. De Morgan, although he appears not to have had multiplication in his mind. s(m  w) will, then, denote whatever is servant of anything of the class composed of men and women taken together. So that w) will, then, denote whatever is servant of anything of the class composed of men and women taken together. So that
s(m  w) = sm w) = sm  sw. sw.
(l  s)w will denote whatever is lover or servant to a woman, and s)w will denote whatever is lover or servant to a woman, and
(l  s)w = lw s)w = lw  sw. sw.
(sl)w will denote whatever stands to a woman in the relation of servant of a lover, and
(sl)w = s(lw).
Thus all the absolute conditions of multiplication are satisfied.
The term "identical with—" is a unity for this multiplication. That is to say, if we denote "identical with—" by 1 we have
x1 = x,
whatever relative term x may be. For what is a lover of something identical with anything, is the same as a lover of that thing.
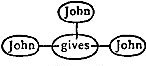
69. A conjugative term like giver naturally requires two correlates, one denoting the thing given, the other the recipient of the gift. We must be able to distinguish, in our notation, the giver of A to B from the giver to A of B, and, therefore, I suppose the signification of the letter equivalent to such a relative to distinguish the correlates as first, second, third, etc., so that "giver of — to —" and "giver to — of —" will be expressed by different letters. Let g denote the latter of these conjugative terms. Then, the correlates or multiplicands of this multiplier cannot all stand directly after it, as is usual in multiplication, but may be ranged after it in regular order, so that
gxy
will denote a giver to x of y. But according to the notation, x here multiplies y, so that if we put for x owner (o), and for y horse (h),
goh
appears to denote the giver of a horse to an owner of a horse. But let the individual horses be H, H', H'', etc. Then
h h is a variable designating an unspecified H. See 84, 94, 111. †1 = H  H' H'  H'' H''  etc. etc.
goh = go(H  H' H'  H'' H''  etc.) = goH etc.) = goH  goH' goH'  goH'' goH''  etc. etc.
Now this last member must be interpreted as a giver of a horse to the owner of that horse, and this, therefore, must be the interpretation of goh. This is always very important. A term multiplied by two relatives shows that the same individual is in the two relations. If we attempt to express the giver of a horse to a lover of a woman, and for that purpose write
glwh,
we have written giver of a woman to a lover of her, and if we add brackets, thus,
g(lw)h,
we abandon the associative principle of multiplication. A little reflection will show that the associative principle must in some form or other be abandoned at this point. But while this principle is sometimes falsified, it oftener holds, and a notation must be adopted which will show of itself when it holds. We already see that we cannot express multiplication by writing the multiplicand directly after the multiplier; let us then affix subjacent numbers after letters to show where their correlates are to be found. The first number shall denote how many factors must be counted from left to right to reach the first correlate, the second how many more must be counted to reach the second, and so on. Then, the giver of a horse to a lover of a woman may be written
g12l1wh = g11l2hw = g2-1hl1w.
70. Of course a negative number indicates that the former correlate follows the latter by the corresponding positive number. A subjacent zero makes the term itself the correlate. Thus,
l0
denotes the lover of that lover or the lover of himself, just as goh denotes that the horse is given to the owner of itself, for to make a term doubly a correlate is, by the distributive principle, to make each individual doubly a correlate, so that
l0 = L0  L0' L0'  L0'' L0''  etc. etc.
A subjacent sign of infinity may indicate that the correlate is indeterminate, so that
l∞
will denote a lover of something. We shall have some confirmation of this presently. See 73. †1
If the last subjacent number is a one it may be omitted. Thus we shall have
l1 = l,
g11 = g1 = g.
This enables us to retain our former expressions lw, goh, etc.
71. The associative principle does not hold in this counting of factors. Because it does not hold, these subjacent numbers are frequently inconvenient in practice, and I therefore use also another mode of showing where the correlate of a term is to be found. This is by means of the marks of reference, † ‡ || § ¶, which are placed subjacent to the relative term and before and above the correlate. Thus, giver of a horse to a lover of a woman may be written
g†‡†l||||w‡h.
The asterisk I use exclusively to refer to the last correlate of the last relative of the algebraic term.
72. Now, considering the order of multiplication to be: — a term, a correlate of it, a correlate of that correlate, etc., — there is no violation of the associative principle. The only violations of it in this mode of notation are that in thus passing from relative to correlate, we skip about among the factors in an irregular manner, and that we cannot substitute in such an expression as goh a single letter for oh. I would suggest that such a notation may be found useful in treating other cases of non-associative multiplication. By comparing this with what was said above In 55. †1 concerning functional multiplication, it appears that multiplication by a conjugative term is functional, and that the letter denoting such a term is a symbol of operation. I am therefore using two alphabets, the Greek and Kennerly, where only one was necessary. But it is convenient to use both.
73. Thus far, we have considered the multiplication of relative terms only. Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives. Now the absolute term "man" is really exactly equivalent to the relative term "man that is —," and so with any other. I shall write a comma after any absolute term to show that it is so regarded as a relative term. Then man that is black will be written
m,b.
But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one. Then
l,sw l, s is the logical product of l and s; ls, on the other hand, is the relative product of l and s. See 54n, 68. †2
will denote a lover of a woman that is a servant of that woman. The comma here after l should not be considered as altering at all the meaning of l, but as only a subjacent sign, serving to alter the arrangement of the correlates. In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates. So
m,,b,r,
means a man that is a rich individual and is a black that is that rich individual. But this has no other meaning than
m,b,r ,
or a man that is a black that is rich. Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number. If, therefore, l,,sw is not the same as l,sw (as it plainly is not, because the latter means a lover and servant of a woman, and the former a lover of and servant of and same as a woman), this is simply because the writing of the comma alters the arrangement of the correlates. And if we are to suppose that absolute terms are multipliers at all (as mathematical generality demands that we should), we must regard every term as being a relative requiring an infinite number of correlates to its virtual infinite series "that is—and is—and is—etc." Now a relative formed by a comma of course receives its subjacent numbers like any relative, but the question is, What are to be the implied subjacent numbers for these implied correlates? Any term may be regarded as having an infinite number of factors, those at the end being ones, thus,
l,sw = l,sw,1,1,1,1,1,1,1, etc.
A subjacent number may therefore be as great as we please. But all these ones denote the same identical individual denoted by w; what then can be the subjacent numbers to be applied to s, for instance, on account of its infinite "that is" 's? What numbers can separate it from being identical with w? There are only two. The first is zero, which plainly neutralizes a comma completely, since
s,0w = sw, A servant of herself who is also a woman is the same as a servant of a woman? †1
and the other is infinity; for as 1∞ is indeterminate in ordinary algebra, so it will be shown hereafter to be here, so that to remove the correlate by the product of an infinite series of ones is to leave it indeterminate. Accordingly,
m,∞
should be regarded as expressing some man. Any term, then, is properly to be regarded as having an infinite number of commas, all or some of which are neutralized by zeros.
"Something" may then be expressed by
1∞. "Something" is whatever is identical with an undetermined thing. †1
I shall for brevity frequently express this by an antique figure one (𝟏).
"Anything" by
10. "Anything" is whatever is identical with itself.†2
I shall often also write a straight 1 for anything.
74. It is obvious that multiplication into a multiplicand indicated by a comma is commutative, It will often be convenient to speak of the whole operation of affixing a comma and then multiplying, as a commutative multiplication, the sign for which is the comma. But though this is allowable, we shall fall into confusion at once if we ever forget that in point of fact it is not a different multiplication, only it is multiplication by a relative whose meaning — or rather whose syntax — has been slightly altered; and that the comma is really the sign of this modification of the foregoing term. †P1 that is,
s,l = l,s.
This multiplication is effectively the same as that of Boole in his logical calculus. Boole's unity is my 1, that is, it denotes whatever is.
75. The sum x + x generally denotes no logical term. But x,∞ + x,∞ may be considered as denoting some two x's. It is natural to write
|
x+x |
= 2.x, |
| and |
x,∞+x,∞ |
= 2.x,∞, |
where the dot shows that this multiplication is invertible. We may also use the antique figures so that
|
2.x,∞ |
= 𝟐x, |
| just as |
1∞ |
= 𝟏. |
Then 𝟐 alone will denote some two things. But this multiplication is not in general commutative, and only becomes so when it affects a relative which imparts a relation such that a thing only bears it to one thing, and one thing alone bears it to a thing. For instance, the lovers of two women are not the same as two lovers of women, that is,
l2.w and 2.lw
are unequal; but the husbands of two women are the same as two husbands of women, that is,
|
h2.w |
= 2.hw, |
| and in general, |
x,2.y |
= 2.x,y. |
76. The conception of multiplication we have adopted is that of the application of one relation to another. So, a quaternion being the relation of one vector to another, the multiplication of quaternions is the application of one such relation to a second. Even ordinary numerical multiplication involves the same idea, for 2 X 3 is a pair of triplets, and 3 X 2 is a triplet of pairs, where "triplet of" and "pair of" are evidently relatives.
If we have an equation of the form
xy = z,
and there are just as many x's per y as there are per things, things of the universe, then we have also the arithmetical equation,
[x][y] = [z].
For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then
[t][f] = [t f]
holds arithmetically. So if men are just as apt to be black as things in general,
[m,][b] = [m,b],
where the difference between [m] and [m,] must not be overlooked. It is to be observed that
[1] = 𝟏.
Boole was the first to show this connection between logic and probabilities. Op. cit., p. 243ff. †1 He was restricted, however, to absolute terms. I do not remember having seen any extension of probability to relatives, except the ordinary theory of expectation.
Our logical multiplication, then, satisfies the essential conditions of multiplication, has a unity, has a conception similar to that of admitted multiplications, and contains numerical multiplication as a case under it.
The Sign of Involution
77. I shall take involution in such a sense that xy will denote everything which is an x for every individual of y. Thus lw will be a lover of every woman. Then (sl)w will denote whatever stands to every woman in the relation of servant of every lover of hers; and s(lw) will denote whatever is a servant of everything that is lover of a woman. So that
(sl)w = s(lw).
A servant of every man and woman will be denoted by sm  w This is more accurately read as: a servant of all those who are either men or women. †1, and sm, sw will denote a servant of every man that is a servant of every woman. So that w This is more accurately read as: a servant of all those who are either men or women. †1, and sm, sw will denote a servant of every man that is a servant of every woman. So that
sm  w = sm,sw. w = sm,sw.
That which is emperor or conqueror of every Frenchman will be denoted by (e  c)f, and ef c)f, and ef  Σpef-p, cp Σpef-p, cp  cf will denote whatever is emperor of every Frenchman or emperor of some Frenchmen and conqueror of all the rest, or conqueror of every Frenchman. Consequently, cf will denote whatever is emperor of every Frenchman or emperor of some Frenchmen and conqueror of all the rest, or conqueror of every Frenchman. Consequently,
(e  c)f = ef c)f = ef  Σpef-p,cp Σpef-p,cp  cf. cf.
Indeed, we may write the binomial theorem so as to preserve all its usual coefficients; for we have
(e  c)f = ef c)f = ef [f].ef-†1,c𝟏† [f].ef-†1,c𝟏† (([f].([f]-𝟏))/𝟐).ef-‡𝟐,c𝟐‡ (([f].([f]-𝟏))/𝟐).ef-‡𝟐,c𝟐‡ etc. Cf. J. N. Lambert. "Sechs Versuche einer Zeichenkunst in der Vernunftlehre"; in Logische u. Philosophische Abhandlungen, vol. 1, ed. J. Bernouilli, Berlin, (1782) for the use of this "Newtonian Formula" in an intensional logic of absolute terms. †2 etc. Cf. J. N. Lambert. "Sechs Versuche einer Zeichenkunst in der Vernunftlehre"; in Logische u. Philosophische Abhandlungen, vol. 1, ed. J. Bernouilli, Berlin, (1782) for the use of this "Newtonian Formula" in an intensional logic of absolute terms. †2
That is to say, those things each of which is emperor or conqueror of every Frenchman consist, first, of all those individuals each of which is a conqueror [emperor!] of every Frenchman; second, of a number of classes equal to the number of Frenchmen, each class consisting of everything which is an emperor of every Frenchman but some one and is a conqueror of that one; third, of a number of classes equal to half the product of the number of Frenchmen by one less than that number, each of these classes consisting of every individual which is an emperor of every Frenchman except a certain two, and is conqueror of those two, etc. This theorem holds, also, equally well with invertible addition, and either term of the binomial may be negative provided we assume
(—x)y = (—)[y].xy.
In addition to the above equations which are required to hold good by the definition of involution, the following also holds,
(s,l)w = sw,lw, I.e., a servant and lover of every woman is a servant of every woman and a lover of every woman.†1
just as it does in arithmetic.
78. The application of involution to conjugative terms presents little difficulty after the explanations which have been given under the head of multiplication. It is obvious that betrayer to every enemy should be written
𝐛a,
just as lover of every woman is written
lw,
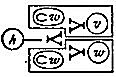
but 𝐛 = 𝐛11 and therefore, in counting forward as the subjacent numbers direct, we should count the exponents, as well as the factors, of the letter to which the subjacent numbers are attached. Then we shall have, in the case of a relative of two correlates, six different ways of affixing the correlates to it, thus:
| 𝐛am |
betrayer of a man to an "The same" substituted for "an"; "some" for "a," "every" for "all" — ink correction on C. S. P.'s own copy; cf. 145.†P1 enemy of him; |
| (𝐛a)m |
betrayer of every man to some enemy of him; |
| 𝐛am |
betrayer of each man to an enemy of every man; |
| 𝐛am |
betrayer of a "The same" substituted for "an"; "some" for "a," "every" for "all" — ink correction on C. S. P.'s own copy; cf. 145.†P1 man to all "The same" substituted for "an"; "some" for "a," "every" for "all" — ink correction on C. S. P.'s own copy; cf. 145.†P1 enemies of all men; |
| 𝐛am |
betrayer of a man to every enemy of him; |
| 𝐛am |
betrayer of every man to every enemy of him. |
If both correlates are absolute terms, the cases are
| 𝐛mw |
betrayer of a woman to a man; |
| (𝐛m)w |
betrayer of each woman to some man; |
| 𝐛mw |
betrayer of all women to a man; |
| 𝐛mw |
betrayer of a woman to every man; "Follows from last because [it is] negative of 𝐛̅mw"—marginal note. †P1 |
| 𝐛mw |
betrayer of a woman to all men; |
| 𝐛mw |
betrayer of every woman to every man. |
These interpretations are by no means obvious, but I shall show that they are correct further on. See 145. †1
79. It will be perceived that the rule still holds here that
(𝐛a)m = 𝐛(am)
that is to say, that those individuals each of which stand to every man in the relation of betrayer to every enemy of his are identical with those individuals each of which is a betrayer to every enemy of a man of that man.
80. If the proportion of lovers of each woman among lovers of other women is equal to the average number of lovers which single individuals of the whole universe have, then
[lw] = [lW'] [lW''] [lW'''] etc.=[l][w].
Thus arithmetical involution appears as a special case of logical involution.
§4. General Formulæ
81. The formulæ which we have thus far obtained, exclusive of mere explanations of signs and of formulæ relating to the numbers of classes, are:
| (1) |
If x ⤙ y and y ⤙ z, then x ⤙ z. |
|
| (2) |
(x  y) y)  z = x z = x  (y (y  z). z). |
(Jevons) |
| (3) |
x  y = y y = y  x. x. |
(Jevons) |
| (4) |
(x  y)z = xz y)z = xz  yz. yz. |
|
| (5) |
x(y  z) = xy z) = xy  xz. xz. |
|
| (6) |
(xy)z = x(yz). |
|
| (7) |
x,(y  z) = x,y z) = x,y  x,z. x,z. |
(Jevons) |
| (8) |
(x,y),z = x,(y,z). |
(Boole) |
| (9) |
x,y, = y,x. |
(Boole) |
| (10) |
(xy)z = x(yz). |
|
| (11) |
xy  z = xy,xz. z = xy,xz. |
|
| (12) |
(x  y)z = xz y)z = xz  Σp(xx-p,yp) Σp(xx-p,yp)  yp yp |
|
= xz [z].xz-†𝟏,y†𝟏 [z].xz-†𝟏,y†𝟏  (([z].[z-𝟏])/𝟐).xz-‡𝟐,y‡𝟐 (([z].[z-𝟏])/𝟐).xz-‡𝟐,y‡𝟐 |
|
 (([z].[z-𝟏].[z-𝟐])/(𝟐.𝟑)).xz-||𝟑,y||𝟑 (([z].[z-𝟏].[z-𝟐])/(𝟐.𝟑)).xz-||𝟑,y||𝟑  etc. etc. |
|
| (13) |
(x,y)z = xz,yz. |
|
| (14) |
x + 0 = x. |
(Boole) |
| (15) |
x1 = x. |
|
| (16) |
(x + y) + z = x + (y + z). |
(Boole) |
| (17) |
x + y = y + x. |
(Boole) |
| (18) |
x + y - y = x. |
(Boole) |
| (19) |
x,(y + z) = x,y + x,z. |
(Boole) |
| (20) |
(x + y)z = x + [z].xz-†1,y†𝟏 + etc. |
|
We have also the following, which are involved implicitly in the explanations which have been given.
| (21) |
x ⤙ x  y. This proposition is the source of the famous so-called paradoxes of material implication. †1 y. This proposition is the source of the famous so-called paradoxes of material implication. †1 |
|
This, I suppose, is the principle of identity, for it follows from this that x = x. This sentence seems to have been misplaced and should have appeared after (22) or (23). †2
| (22) |
x  x = x. x = x. |
(Jevons) |
| (23) |
x,x = x. |
(Boole) |
| (24) |
x  y = x + y - x,y. y = x + y - x,y. |
|
The principle of contradiction is
where n stands for "not." The principle of excluded middle is
| (26) |
x  nx = 1. nx = 1. |
|
It is an identical proposition, that, if φ be determinative, we have
The six following are derivable from the formulæ already given:
| (28) |
(x  y),(x y),(x  z) = x z) = x  y,z. y,z. |
|
| (29) |
(x - y)  (z - w) = (x (z - w) = (x  z)-(y z)-(y  w) + y,z,(1-w) + x,(1 - y),w. w) + y,z,(1-w) + x,(1 - y),w. |
|
In the following, φ is a function involving only the commutative operations and the operations inverse to them.
| (30) |
φx = (φ1),x + (φ0),(1 - x). |
(Boole) |
| (31) |
φx = (φ1 (1-x)),(φ0 (1-x)),(φ0 x). x). |
|
| (32) |
If φx = 0 (φ1),(φ0) = 0. |
(Boole) |
| (33) |
If φx = 1 φ1  φ0 = 1. φ0 = 1. |
|
The reader may wish information concerning the proofs of formulæ (30) to (33). When involution is not involved in a function nor any multiplication except that for which x,x=x, it is plain that φx is of the first degree, and therefore, since all the rules of ordinary algebra hold, we have as in that
φx = φ0 + (φ1 - φ0),x.
We shall find, hereafter, that when y has a still more general character, we have,
φx = φ0 + (φ1 - φ0)x.
The former of these equations by a simple transformation gives (30).
If we regard (φ1), (φ0) as a function of x and develop it by (30), we have
(φ1),(φ0) = x,(φ1),(φ0) + (φ1),(φ0),(1-x).
Comparing these terms separately with the terms of the second member of (30), we see that
(φ1),(φ0) ⤙ x.
This gives at once (32), and it gives (31) after performing the multiplication indicated in the second member of that equation and equating φx to its value as given in (30). If (φ1  φ0) is developed as a function of x by (31), and the factors of the second member are compared with those of the second member of (31), we get φ0) is developed as a function of x by (31), and the factors of the second member are compared with those of the second member of (31), we get
φx ⤙ φ1  φ0, φ0,
from which (33) follows immediately.
Properties of Zero and Unity
82. The symbolical definition of zero is
x+0 = x,
| so that by (19) |
x,a = x,(a+0) = x,a+x,0. |
Hence, from the invertible character of this addition, and the generality of (14), we have
x,0 = 0.
By (24) we have in general,
|
x  0 = x + 0 - x,0 = 0 = x + 0 - x,0 = |
x, |
| or |
x  0 = 0 = |
x. |
| By (4) we have |
a x = (a  0)x = 0)x = |
a x  0x. 0x. |
| But if a is an absurd relation, |
a x = |
0, |
| so that |
0x = |
0, |
| which must hold invariably. |
|
|
| From (12) we have |
ax = (a  0)x = ax 0)x = ax  0x 0x  etc., etc., |
| whence by (21) |
0x ⤙ ax. I.e., by (21) 0x ⤙ ax 0x and as by (12) ax + 0x = ax, 0x ⤙ ax. †1 |
But if a is an absurd relation, and x is not zero,
ax = 0.
| And therefore, unless x=0, |
0x = 0. |
83. Any relative x may be conceived as a sum of relatives X, X', X'', etc., such that there is but one individual to which anything is X, but one to which anything is X', etc. Thus, if x denote "cause of," X,X',X'' would denote different kinds of causes, the causes being divided according to the differences of the things they are causes of. Then we have
X y = X(y  0) = X y 0) = X y  X0, X0,
whatever y may be. Hence, since y may be taken so that
and in a similar way,
| X'0 = 0, |
X''0 = 0, X'''0 = 0, etc. |
We have, then,
x0 = (X  X' X'  X'' X''  X''' X'''  etc.)0 etc.)0
= X0  X'0 X'0  X''0 X''0  X'''0 X'''0  etc. = 0. etc. = 0.
84. If the relative x be divided in this way into X,X',X'', X''', etc., so that x is that which is either X or X' or X'' or X''', etc., then non-x is that which is at once non-X and non-X' and non-X'', etc.; that is to say,
non-x = non-X, non-X', non-X'', non-X''', etc.;
where non-X is such that there is something (Z) such that everything is non-X to Z; and so with non-X', non-X'', etc. Now, non-x may be any relative whatever. Substitute for it, then, y; and for non-X, non-X', etc., Y,Y', etc. Then we have
| y = Y,Y',Y'',Y''', etc.; |
| and |
Y'Z' = 1, |
Y''Z'' = 1, |
Y'''Z''' = 1, |
etc., |
where Z',Z'',Z''' are individual terms which depend for what they denote on Y',Y'',Y'''.
Then we have
1 = Y'Z' = Y'Z' = Y'(Z'  0) = Y'Z',Y'0 = Y'Z',Y'0, 0) = Y'Z',Y'0 = Y'Z',Y'0, |
| or Y'0 = 1, |
Y''0 = 1, |
Y'''0= 1, |
etc. |
| Then |
y0 = (Y', Y'', Y''', etc.)0 = Y'0, Y''0, Y'''0, etc. = 1. |
| We have by definition, |
x1 = |
x. |
| Hence, by (6), |
a x = (a1)x = |
a(1x). |
Now a may express any relation whatever, but things the same way related to everything are the same. Hence,
|
x = |
1x. |
| We have by definition, |
1 = |
1[0]. |
| Then if X is any individual |
X,1 = |
X,1[0] = X,1X. |
| But |
1X = |
X. |
| Hence |
X,1 = |
X,X; |
| and by (23) |
X,1 = |
X; |
| whence if we take |
x = |
X + X' + X'' + X''' + etc., |
where X,X' etc, denote individuals (and by the very meaning of a general term this can always be done, whatever x may be)
|
x,1 = (X + X' + X'' + etc.),1 = X,1 + X',1 + X'',1 + etc. |
|
= X + X' + X'' + etc. = x, |
| or |
x,1 = x. |
| We have by (24) |
x  1 = x + 1 - x,1 = x + 1 - x = 1, 1 = x + 1 - x,1 = x + 1 - x = 1, |
| or |
x  1 = 1. 1 = 1. |
85. We may divide all relatives into limited and unlimited. Limited relatives express such relations as nothing has to everything. For example, nothing is knower of everything. Unlimited relatives express relations such as something has to everything. For example, something is as good as anything. For limited relatives, then, we may write
p1 = 0.
The converse of an unlimited relative expresses a relation which everything has to something. Thus, everything is as bad as something. Denoting such a relative by q,
q1 = 1.
These formulæ remind one a little of the logical algebra of Boole; because one of them holds good in arithmetic only for zero, and the other only for unity.
| We have by (10) |
1x = (q0)x = q(0x) = q0 = 1, |
| or |
1x = 1. |
| We have by (4) |
1x = (a  1)x = a x 1)x = a x  1x, 1x, |
| or by (21) |
a x ⤙ 1x. |
But everything is somehow related to x unless x is 0; hence unless x is 0,
1x = 1.
If a denotes "what possesses," and y "character of what is denoted by x,"
|
x = ay = a(y1) = (ay)1 = |
x1, |
| or |
x1 = |
x. |
Since 1 means "identical with," l,1w denotes whatever is both a lover of and identical with a woman, or a woman who is a lover of herself. And thus, in general,
x,1 = x[0],.
86. Nothing is identical with every one of a class; and therefore 1x is zero, unless x denotes only an individual when 1x becomes equal to x. But equations founded on interpretation may not hold in cases in which the symbols have no rational interpretation.
Collecting together all the formulæ relating to zero and
unity, we have
| (34) |
x  0 = x. 0 = x. |
(Jevons) |
| (35) |
x  1 = 1. 1 = 1. |
(Jevons) |
| (36) |
x0 = 0. |
|
| (37) |
0x = 0. |
|
| (38) |
x,0 = 0. |
(Boole) |
| (39) |
x0 = 1. |
|
| (40) |
0x = 0, provided x > 0. On his own copy, Peirce substitutes the condition "x is an unlimited relative," for "x > 0." †1 |
|
| (41) |
1x = x. |
|
| (42) |
x,1 = x0,. |
|
| (43) |
x1 = x. |
|
| (44) |
1x = 0, unless x is individual, when 1x = x. |
|
| (45) |
q1 = 1, where q is the converse of an unlimited relative. |
| (46) |
1x = 1, provided x > 0. See 145. †1 |
|
| (47) |
x,1 = x. |
(Boole) |
| (48) |
p1 = 0, where p is a limited relative. |
|
| (49) 1 |
x = 1. |
These, again, give us the following:
| (50) |
0  1 = 1 1 = 1 |
(64) |
01=0 |
| (51) |
0  1 = 1 1 = 1 |
(65) |
1 1=1 |
| (52) |
00 = 0 |
(66) |
1,1=1 |
| (53) |
0,0 = 0 |
(67) |
11=1 |
| (54) |
00 = 1 |
(68) |
11 = 1 |
| (55) |
10 = 0 |
(69) |
1,1 = 1 |
| (56) |
01 = 0 |
(70) |
11 = 1 |
| (57) |
0,1 = 0 |
(71) |
11=1 |
| (58) |
01 = 0 |
(72) |
11 = 1 |
| (59) |
10 = 1 |
(73) |
1,1 = 1 |
| (60) |
01 = 0 |
(74) |
11 = 1 |
| (61) |
10 = 0 |
(75) |
11 = 0 |
| (62) |
0,1 = 0 |
(76) |
1, = 1 |
| (63) |
10 = 1 |
|
|
From (64) we may infer that 0 is a limited relative, and from (60) that it is not the converse of an unlimited relative. From (70) we may infer that 1 is not a limited relative, and from (68) that it is the converse of an unlimited relative.
Formulæ Relating to the Numbers of Terms
87. We have already seen that
| (77) |
If x ⤙ y, then [x] ⤙ [y]. |
| (78) |
When x,y = 0, then [x  y] = [x] y] = [x]  [y], [y], |
| (79) |
When [xy]:[nxy] = [x]:[nx], then [xy] = [x][y]. |
| (80) |
When [x𝖓y] = [x][𝖓y][1], then [x y] = [x][y]. |
It will be observed that the conditions which the terms must conform to, in order that the arithmetical equations shall hold, increase in complexity as we pass from the more simple relations and processes to the more complex.
88. We have seen that
| (81) |
[0] = 0. |
| (82) |
[1] = 1. |
Most commonly the universe is unlimited, and then
| (83) |
[1] = ∞; See 198. †1 |
and the general properties of 1 correspond with those of infinity. Thus,
x  1 = 1 1 = 1 |
corresponds to |
x + ∞ = ∞, |
| q1 = 1 |
corresponds to |
q ∞ = ∞, |
| 1x = 1 |
corresponds to |
∞ x= ∞, |
| p1 = 0 |
corresponds to |
p ∞ = 0, |
| 1x = 1 |
corresponds to |
∞ x = ∞. |
The formulæ involving commutative multiplication are derived from the equation 1, = 1. But if 1 be regarded as infinite, it is not an absolute infinite; for 10 = 0. On the other hand, 11 = 0.
It is evident, from the definition of the number of a term, that
We have, therefore, if the probability of an individual being x to any y is independent of what other y's it is x to, and if x is independent of y,
§5. General Method of Working with This Notation
89. Boole's logical algebra contains no operations except our invertible addition and commutative multiplication, together With the corresponding subtraction and division. He has, therefore, only to expand expressions involving division, by means of (30), so as to free himself from all non-determinative operations, in order to be able to use the ordinary methods of algebra, which are, moreover, greatly simplified by the fact that
x,x = x.
90. Mr. Jevons's modification In his Pure Logic. †1 of Boole's algebra involves only non-invertible addition and commutative multiplication, without the corresponding inverse operations. He is enabled to replace subtraction by multiplication, owing to the principle of contradiction, and to replace division by addition, owing to the principle of excluded middle. For example, if x be unknown, and we have
x  m = a, m = a,
or what is denoted by x together with men make up animals, we can only conclude, with reference to x, that it denotes (among other things, perhaps) all animals not men; that is, that the x's not men are the same as the animals not men. Let m̅ denote non-men; then by multiplication we have
xm̅,  m,m̅ = x,m̅ = a,m̅, m,m̅ = x,m̅ = a,m̅,
because, by the principle of contradiction,
m,m̅ = 0.
Or, suppose, x being again unknown, we have given
a,x = m.
Then all that we can conclude is that the x's consist of all the m's and perhaps some or all of the non-a's, or that the x's and non-a's together make up the m's and non-a's together. If, then, ā denote non-a, add ā to both sides and we have
|
a,x  ā = m ā = m  ā. ā. |
| Then by (28) |
(a  ā),(x ā),(x  ā) = m ā) = m  ā. ā. |
But by the principle of excluded middle,
|
a  ā = 1 ā = 1 |
| and therefore |
x  ā = m ā = m  ā. ā. |
I am not aware that Mr. Jevons actually uses this latter process, but it is open to him to do so. In this way, Mr. Jevons's algebra becomes decidedly simpler even than Boole's.
It is obvious that any algebra for the logic of relatives must be far more complicated. In that which I propose, we labor under the disadvantages that the multiplication is not generally commutative, that the inverse operations are usually indeterminative, and that transcendental equations, and even equations like
abx = cdex + fx + x,
where the exponents are three or four deep, are exceedingly common. It is obvious, therefore, that this algebra is much less manageable than ordinary arithmetical algebra.
91. We may make considerable use of the general formulæ already given, especially of (1), (21), and (27), and also of the following, which are derived from them:
| (86) |
If a ⤙ b |
then there is such a term x that a  x = b. x = b. |
| (87) |
If a ⤙ b |
then there is such a term x that b,x = a. |
| (88) |
If b,x = a |
then a ⤙ b. |
| (89) |
If a ⤙ b |
c  a ⤙ c a ⤙ c  b. b. |
| (90) |
If a ⤙ b |
ca ⤙ cb. |
| (91) |
If a ⤙ b |
ac ⤙ bc. |
| (92) |
If a ⤙ b |
cb ⤙ ca Where c = not, this becomes the formula for contraposition. See 142 and 2.550. In 186, however, a different formula for contraposition is given. †1 |
| (93) |
If a ⤙ b |
ac ⤙ bc. |
| (94) |
a,b ⤙ a |
|
There are, however, very many cases in which the formulæ thus far given are of little avail.
92. Demonstration of the sort called mathematical is founded on suppositions of particular cases. The geometrician draws a figure; the algebraist assumes a letter to signify a single quantity fulfilling the required conditions. But while the mathematician supposes an individual case, his hypothesis is yet perfectly general, because he considers no characters of the individual case but those which must belong to every such case. The advantage of his procedure lies in the fact that the logical laws of individual terms are simpler than those which relate to general terms, because individuals are either identical or mutually exclusive, and cannot intersect or be subordinated to one another as classes can. Mathematical demonstration is not, therefore, more restricted to matters of intuition than any other kind of reasoning. Indeed, logical algebra conclusively proves that mathematics extends over the whole realm of formal logic; and any theory of cognition which cannot be adjusted to this fact must be abandoned. We may reap all the advantages which the mathematician is supposed to derive from intuition by simply making general suppositions of individual cases.
93. In reference to the doctrine of individuals, Cf. the definition of individuals in 611-13.†1 two distinctions should be borne in mind. The logical atom, or term not capable of logical division, must be one of which every predicate may be universally affirmed or denied. For, let A be such a term. Then, if it is neither true that all A is X nor that no A is X, it must be true that some A is X and some A is not X; and therefore A may be divided into A that is X and A that is not X, which is contrary to its nature as a logical atom. Such a term can be realized neither in thought nor in sense. Not in sense, because our organs of sense are special — the eye, for example, not immediately informing us of taste, so that an image on the retina is indeterminate in respect to sweetness and non-sweetness. When I see a thing, I do not see that it is not sweet, nor do I see that it is sweet; and therefore what I see is capable of logical division into the sweet and the not sweet. It is customary to assume that visual images are absolutely determinate in respect to color, but even this may be doubted. I know no facts which prove that there is never the least vagueness in the immediate sensation. In thought, an absolutely determinate term cannot be realized, because, not being given by sense, such a concept would have to be formed by synthesis, and there would be no end to the synthesis because there is no limit to the number of possible predicates. A logical atom, then, like a point in space, would involve for its precise determination an endless process. We can only say, in a general way, that a term, however determinate, may be made more determinate still, but not that it can be made absolutely determinate. Such a term as "the second Philip of Macedon" is still capable of logical division—into Philip drunk and Philip sober, for example; but we call it individual because that which is denoted by it is in only one place at one time. It is a term not absolutely indivisible, but indivisible as long as we neglect differences of time and the differences which accompany them. Such differences we habitually disregard in the logical division of substances. In the division of relations, etc., we do not, of course, disregard these differences, but we disregard some others. There is nothing to prevent almost any sort of difference from being conventionally neglected in some discourse, and if I be a term which in consequence of such neglect becomes indivisible in that discourse, we have in that discourse,
[I] = 1.
This distinction between the absolutely indivisible and that which is one in number from a particular point of view is shadowed forth in the two words individual {to atomon} and singular {to kath' hekaston}; but as those who have used the word individual have not been aware that absolute individuality is merely ideal, it has come to be used in a more general sense. The absolute individual can not only not be realized in sense or thought, but cannot exist, properly speaking. For whatever lasts for any time, however short, is capable of logical division, because in that time it will undergo some change in its relations. But what does not exist for any time, however short, does not exist at all. All, therefore, that we perceive or think, or that exists, is general. So far there is truth in the doctrine of scholastic realism. But all that exists is infinitely determinate, and the infinitely determinate is the absolutely individual. This seems paradoxical, but the contradiction is easily resolved. That which exists is the object of a true conception. This conception may be made more determinate than any assignable conception; and therefore it is never so determinate that it is capable of no further determination. †P1
94. The old logics distinguish between individuum signatum and individuum vagum. "Julius Cæsar" is an example of the former; "a certain man," of the latter. The individuum vagum, in the days when such conceptions were exactly investigated, occasioned great difficulty from its having a certain generality, being capable, apparently, of logical division. If we include under the individuum vagum such a term as "any individual man," these difficulties appear in a strong light, for what is true of any individual man is true of all men. Such a term is in one sense not an individual term; for it represents every man. But it represents each man as capable of being denoted by a term Which is individual; and so, though it is not itself an individual term, it stands for any one of a class of individual terms. If we call a thought about a thing in so far as it is denoted by a term, a second intention, we may say that such a term as "any individual man" is individual by second intention. The letters which the mathematician uses (whether in algebra or in geometry) are such individuals by second intention. Such individuals are one in number, for any individual man is one man; they may also be regarded as incapable of logical division, for any individual man, though he may either be a Frenchman or not, is yet altogether a Frenchman or altogether not, and not some one and some the other. Thus, all the formal logical laws relating to individuals will hold good of such individuals by second intention, and at the same time a universal proposition may at any moment be substituted for a proposition about such an individual, for nothing can be predicated of such an individual which cannot be predicated of the whole class.
95. There are in the logic of relatives three kinds of terms which involve general suppositions of individual cases. The first are individual terms, which denote only individuals See 96ff. †1; the second are those relatives whose correlatives are individual: I term these infinitesimal relatives See 100ff. †2; the third are individual infinitesimal relatives, and these I term elementary relatives. See 121ff. †3
Individual Terms
96. The fundamental formulæ relating to individuality are two. Individuals are denoted by capitals.
| (95) |
If x > 0 x = X  X' X'  X'' X''  X''' X'''  etc. etc. |
| (96) |
yX = yX. |
We have also the following which are easily deducible from these two:
| (97) (y,z)X = (y X),(z X). |
(99) [X] = 𝟏. |
| (98) X,y0 = X,y X. |
(100) 1X = X. |
We have already seen that
1x = 0, provided that [x] > 𝟏.
97. As an example of the use of the formulæ we have thus far obtained, let us investigate the logical relations between "benefactor of a lover of every servant of every woman," "that which stands to every servant of some woman in the relation of benefactor of a lover of him," "benefactor of every lover of some servant of a woman," "benefactor of every lover of every servant of every woman," etc.
In the first place, then, we have by (95)
sw = s(W'  W'' W''  W''' W'''  etc.) = sW' etc.) = sW'  sW'' sW''  sW''' sW'''  etc. etc.
sw = sW'  W'' W''  W''' W'''  etc. = sW' etc. = sW'  sW'' sW''  sW''' sW'''  etc. etc.
From the last equation we have by (96)
sw = (sW'),(sW''),(sW'''), etc.
| Now by (31) |
x'  x'' x''  etc. = x',x",x"', etc. etc. = x',x",x"', etc.  etc., etc., |
| or |
|
| (101) |
Π' ⤙ Σ', |
where Π' and Σ' signify that the addition and multiplication with commas Π' signifies logical multiplication and Σ' signifies logical addition. †1 are to be used. From this it follows that
| (102) |
sw ⤙ sw. A servant of every woman is a servant of a woman. †2 |
If w vanishes, this equation fails, because in that case (95) does not hold.
| From (102) we have |
|
|
| (103) |
(ls)w ⤙ |
lsw. A lover-of-a-servant of every woman is a lover-of-a-servant of a woman. †3 |
| Since |
a = |
a,b  etc., etc., |
|
b = |
a,b  etc., etc., |
| we have |
la = |
l(a,b  etc.) = l(a,b) etc.) = l(a,b)  l (etc.), l (etc.), |
|
lb = |
l(a,b  etc.) = l(a,b) etc.) = l(a,b)  l (etc.). l (etc.). |
Multiplying these two equations commutatively we have
(la),(lb) = l(a,b)  etc. etc.
or
| (104) |
lΠ' ⤙ Π'l. See Lewis' Survey of Symbolic Logic, p. 87n for a proof of this theorem. †1 |
| Now |
(ls)w = (s)W'  W'' W''  W''' W'''  etc. = Π'(ls)W = Π'lsW, etc. = Π'(ls)W = Π'lsW, |
|
lsw = lsW'  W'' W''  W''' W'''  etc. = lΠ'sW' = lΠ'sW. etc. = lΠ'sW' = lΠ'sW. |
| Hence, |
|
| (105) |
lsw ⤙ (ls)w, |
or every lover of a servant of all women stands to every woman in the relation of lover of a servant of hers.
| From (102) we have |
|
| (106) |
lsw ⤙ lsw. A lover of every servant of all women is a lover of a servant of every woman. †2 |
| By (95) and (96) we have |
| lsw = |
ls(W'  W'' W''  W''' etc.) = lsW' W''' etc.) = lsW'  lsW'' lsW''  lsW''' lsW'''  etc. etc. |
|
= lsW'  lsW'' lsW''  lsW''' + etc. lsW''' + etc. |
| Now |
sW = sW' W'' W''  W''' W'''  etc. = sW',sW'',sW''', etc. etc. = sW',sW'',sW''', etc. |
| So that by (94) |
sw ⤙ sW' ⤙ sW'. |
| Hence by (92) |
|
|
lsW' ⤙ lsw, lsW'' ⤙ lsw lsW''' ⤙ lsw. |
| Adding, |
lsW'  lsW'' lsW''  lsW''' ⤙ lsw; lsW''' ⤙ lsw; |
| or |
|
| (107) |
lsw ⤙ lsw. |
That is, every lover of every servant of any particular woman is a lover of every servant of all women.
| By (102) we have |
|
| (108) |
lsw ⤙ lsw. A lover of every servant-of-a-woman is to a woman a lover of all her servants.†3 |
| Thus we have |
|
| lsw ⤙ lsw ⤙ lsw ⤙ lsw ⤙ (ls)w ⤙ lsw. lsw ⤙ lsw and lsw ⤙ (ls)w invariably holds—marginal note. †P1 |
98. By similar reasoning we can easily make out the relations shown in the following table. It must be remembered
that the formulæ do not generally hold when exponents vanish.  On Peirce's copy a line was drawn through the vinculum in each of these cases with the comment, "Crossed are not universally true." †1 On Peirce's copy a line was drawn through the vinculum in each of these cases with the comment, "Crossed are not universally true." †1
99. It appears to me that the advantage of the algebraic notation already begins to be perceptible, although its powers are thus far very imperfectly made out. At any rate, it seems to me that such a prima facie case is made out that the reader who still denies the utility of the algebra ought not to be too indolent to attempt to write down the above twenty-two terms in ordinary language With logical precision. Having done that, he has only to disarrange them and then restore the arrangement by ordinary logic, in order to test the algebra so far as it is yet developed.
Infinitesimal Relatives
100. We have by the binomial theorem by (49) and by (47),
(1 +x)n = 1 + Σpxn-p + xn.
Now, if we suppose the number of individuals to which any one thing is x to be reduced to a smaller and smaller number, we reach as our limit
x𝟐 = 0,
Σpxn-p = [n].𝟏n-†𝟏,x†𝟏 = xn,
(1 + x)n = 1 + x n.
101. If, on account of the vanishing of its powers, we call x an infinitesimal here and denote it by i, and if we put
x n = i n = y,
our equation becomes
| (109) |
(1 +i) (y/i) = 1 + y. |
Putting y = 1, and denoting (1 + i)(1/i) by  , we have , we have
| (110) |
 = (1 +i)1/i = 1 + 1. = (1 +i)1/i = 1 + 1. |
102. In fact, this agrees With ordinary algebra better than it seems to do; for 1 is itself an infinitesimal, and  is is  1. If the higher powers of 1 did not vanish, we should get the ordinary development of 1. If the higher powers of 1 did not vanish, we should get the ordinary development of  . .
103. Positive powers of  are absurdities in our notation. For negative powers we have are absurdities in our notation. For negative powers we have
| (111) |
 -x = 1 - x. -x = 1 - x. |
104. There are two ways of raising  -x to the yth power. In the first place, by the binomial theorem, -x to the yth power. In the first place, by the binomial theorem,
(1-x)y = 1-[y].1y-†𝟏,x†𝟏 + ([y].[y-𝟏]/𝟐).1y-‡𝟑,x‡𝟐—etc.;
and, in the second place, by (111) and (10).
 -xy = 1 - xy. I.e., 1-(xy). †1 -xy = 1 - xy. I.e., 1-(xy). †1
It thus appears that the sum of all the terms of the binomial development of (1-x)y, after the first, is -xy. I.e., -(xy). †2 The truth of this may be shown by an example. Suppose the number of y's are four, viz. Y', Y'', Y''', and Y''''. Let us use x', x'', x''', and x'''' in such senses that
| x Y' = x', |
x Y'' = x'', |
x Y''' = x''', |
x Y'''' = x''''. |
Then the negatives of the different terms of the binomial developement are,
[y].1y-†𝟏,x†𝟏 = x' + x'' + x''' + x''''.
-(([y].[y-𝟏])/𝟐).1y-‡𝟐,x‡𝟐 = -x',x''-x',x'''-x',x''''-x'',x'''-x'',x''''-x''',x''''. I.e., -(x', x'') - (x', x''') etc. †3
+(([y].[y-𝟏][y-𝟐])/𝟐.𝟑).1-||𝟑x||𝟑 = x',x'',x'''+ x',x'',x'''' + x',x''',x'''' + x'',x''',x''''.
xy = -x', x'', x''''. I.e., -(x', x'', x''', x'''').†4
Now, since this addition is invertible, in the first term, x' that is x'', is counted over twice, and so with every other pair. The second term subtracts each of these pairs, so that it is only counted once. But in the first term the x' that is x'' that is x''' is counted in three times only, while in the second term it is subtracted three times; namely, in (x',x''), in (x',x''') and in (x'',x'''). On the whole, therefore, a triplet would not be represented in the sum at all, were it not added by the third term. The whole quartette is included four times in the first term, is subtracted six times by the second term, and is added four times in the third term. The fourth term subtracts it once, and thus in the sum of these negative terms each combination occurs once, and once only; that is to say the sum is
x'  x'' x''  x''' x'''  x'''' = x(Y' x'''' = x(Y'  Y'' Y''  Y''' Y'''  Y'''') = xy. Y'''') = xy.
105. If we write (a x)𝟑 for [x].[x-𝟏].[x-𝟐].1x-†𝟑,a†𝟑, that is for whatever is a to any three x's, regard being had for the order of the x's; and employ the modern numbers as exponents with this signification generally, then
1 - a x + (𝟏/𝟐!)(a x)2 - (𝟏/𝟑!)(a x)3 + etc.
is the development of (1 - a)x and consequently it reduces itself to 1 - a x. That is,
| (112) |
x = x - (𝟏/𝟐!)x2 + (𝟏/𝟑!)x3 + (𝟏/𝟒!)x4 +etc. |
106. 1 - x denotes everything except x, that is, whatever is other than every x; so that  - means "not." We shall take log x in such a sense that - means "not." We shall take log x in such a sense that
 log x = x. It makes another resemblance between 1 and infinity that log 0 = -1. †P1 log x = x. It makes another resemblance between 1 and infinity that log 0 = -1. †P1
107. I define the first difference of a function by the usual formula,
| (113) |
Δφx = φ(x + Δx) - φx, |
where Δx is an indefinite relative which never has a correlate in common with x. So that
| (114) |
x,(Δx) = 0 |
x + Δx = x  Δx. Δx. |
Higher differences may be defined by the formulæ
| (115) |
Δ𝖓·x = 0 if 𝖓 > 1
Δ2.φx =ΔΔx = φ(x+𝟐.Δx)-𝟐.φ(x+Δx)+φx,
Δ3·φx = ΔΔ2.x = φ(x+𝟑.Δx)-𝟑.φ(x+𝟐.Δx)+𝟑.φ(x+Δx)-φx. |
| (116) |
Δ𝖓·φx = φ(x+𝖓.Δx)-𝖓.φ(x+(𝖓-𝟏).Δx)
+ (𝖓.(𝖓-𝟏))/𝟐.φ(x+(𝖓-𝟐).Δx) - etc. |
108. The exponents here affixed to Δ denote the number of times this operation is to be repeated, and thus have quite a different signification from that of the numerical coefficients in the binomial theorem. I have indicated the difference by putting a period after exponents significative of operational repetition. Thus, m2 may denote a mother of a certain pair, m2. a maternal grandmother.
109. Another circumstance to be observed is, that in taking the second difference of x, if we distinguish the two increments which x successively receives as Δ'x and Δ''x, then by (114)
(Δ'x),(Δ''x) = 0
If Δx is relative to so small a number of individuals that if the number were diminished by one Δ𝖓·φx would vanish, then I term these two corresponding differences differentials, and write them with 𝐝 instead of Δ.
110. The difference of the invertible sum of two functions is the sum of their differences; for by (113) and (18),
(117) Δ(φx + ψx) = φ(x + Δx) + ψ(x + Δx) - φx - ψx
= φ(x + Δx) - φx + ψ(x + Δx) - ψx = Δψx + Δψx. |
If a is a constant, we have
| (118) |
Δaφx = a(φx  Δφx) - aφx = aΔφx - (aΔφx),aφx, Δφx) - aφx = aΔφx - (aΔφx),aφx, |
|
Δ2.aφx = -Δaφx,aΔx, etc. |
|
Δ(φx)a = (Δφx)a - ((Δφx)a),φxa, |
|
Δ2.(φx)a = -Δ(φx)a, etc. |
| (119) |
φ(a,φx) = a,Δφx. |
Let us differentiate the successive powers of x. We have in the first place,
Δ(x𝟐) = (x + Δx)𝟐 - x𝟐 = 𝟐.x𝟐-†𝟏,(Δx)†𝟏 + (Δx)𝟐.
Here, if we suppose Δx to be relative to only one individual, (Δx)𝟐 vanishes, and we have, with the aid of (115),
𝐝(x𝟐) = 𝟐.x𝟏,𝐝x .
Considering next the third power, we have, for the first differential,
Δ(x𝟑) = (x + Δx)𝟑 - x𝟑 = 𝟑.x𝟑-†𝟏,(Δx)†𝟏 + 𝟑.x𝟑-‡𝟐,(Δx)‡𝟐+(Δx)𝟑, 𝐝(x𝟑) = 𝟑.x𝟐,𝐝(x).
To obtain the second differential, we proceed as follows:
| Δ𝟐.(x𝟑) |
= (x + 𝟑.Δx)𝟑 - 𝟐.(x + Δx)𝟑 + x𝟑 |
|
= x𝟑 + 𝟔.x𝟑-†𝟏,(Δx)†𝟏 + 𝟏𝟐.x𝟑-‡𝟐,(Δx)‡𝟐 + 𝟖.(Δx)𝟑 |
|
- 𝟐.x𝟑 - 𝟔.x𝟑-||𝟏,(Δx)||𝟏 - 𝟔.x𝟑-§𝟐,(Δx)§𝟐 - 2.(Δx)𝟑 + x𝟑 |
|
= 𝟔.x𝟑-‡𝟐,(Δx)‡𝟐 + 𝟔.(Δx)𝟑. |
Here, if Δx is relative to less than two individuals, Δφx vanishes. Making it relative to two only, then, we have
𝐝𝟐.(x𝟑) = 𝟔.x𝟏,(𝐝x)𝟐.
These examples suffice to show what the differentials of x𝖓 will be. If for the number 𝖓 we substitute the logical term n, we have
Δ(xn) = (x + Δx)n - xn = [n].xn-†𝟏,(Δx)†𝟏 + etc.
𝐝(xn) = [n].xn-𝟏,(𝐝x).
We should thus readily find
| (120) |
𝐝𝖒·(xn) = [n].[n-𝟏].[n-𝟐]....[n-𝖒+𝟏].xn-†𝖒,(𝐝x)†𝖒. |
Let us next differentiate lx. We have, in the first place,
Δlx = lx  Δx - lx = lx,lΔx - lx = lx,(lΔx - 1). Δx - lx = lx,lΔx - lx = lx,(lΔx - 1).
The value of lΔ'x - 1 is next to be found.
| We have by (111) |
 lΔx - 1 = lΔx. lΔx - 1 = lΔx. |
| Hence, |
lΔx - 1 = log lΔx. |
| But by (10) |
log lΔx = (log l)Δx. |
Substituting this value of l𝐝x - 1 in the equation lately found for 𝐝lx we have
| (121) |
𝐝lx = lx,(log,l) 𝐝x = lx,(l - 1) 𝐝x = -lx,(1 - l) 𝐝x. |
111. In printing this paper, I here make an addition which supplies an omission in the account given above In 56. †1 of involution in this algebra. We have seen that every term which does not vanish is conceivable as logically divisible into individual terms. Thus we may write
s = S' S'' S''  S''' S'''  etc. etc.
where not more than one individual is in any one of these relations to the same individual, although there is nothing to prevent the same person from being so related to many individuals. I.e., each correlate has only one relate though a given relate may have many correlates. †1 Thus, "bishop of the see of" may be divided into first bishop, second bishop, etc., and only one person can be 𝖓th bishop of any one see, although the same person may (where translation is permitted) be 𝖓th bishop of several sees. Now let us denote the converse of x by 𝐊x; thus, if s is "servant of," 𝐊s is "master or mistress of." Then we have
𝐊s = 𝐊S'  𝐊S'' 𝐊S''  𝐊S''' 𝐊S'''  etc.; etc.;
and here each of the terms of the second member evidently expresses such a relation that the same person cannot be so related to more than one, although more than one may be so related to the same. Thus, the converse of "bishop of the see of —" is "see one of whose bishops is —," the converse of "first bishop of —" is "see whose first bishop is —," etc. Now, the same see cannot be a see whose 𝖓th bishop is more than one individual, although several sees may be so related to the same individual. Such relatives I term infinitesimal on account of the vanishing of their higher powers. Every relative has a converse, and since this converse is conceivable as divisible into individual terms, the relative itself is conceivable as divisible into infinitesimal terms. To indicate this we may write
| (122) |
If x > 0 x = X,  X,, X,,  X,,, X,,,  etc. etc. |
112. As a term which vanishes is not an individual, nor is it composed of individuals, so it is neither an infinitesimal nor composed of infinitesimals.
| As we write |
l S',l S'',l S''', etc. = ls, |
| so may we write |
|
| (123) |
L,s,L,,s,L,,,s, etc. = ls, |
But as the first formula is affected by the circumstance that zero is not an individual, so that lsw does not vanish on account of no woman having the particular kind of servant denoted by S'', lsw denoting merely every lover of whatever servant there is of any woman; so the second formula is affected in a similar way, so that the vanishing of L[,]s does not make ls to vanish, but this is to be interpreted as denoting everything which is a lover, in whatever way it is a lover at all, of a servant. I.e., as a lover of none but servants. †1 Then just as we have by (112), that
| (124) |
ls = 1 - (1 - l)s; A lover of all servants is not a non-lover of a servant, †2 |
| so we have |
|
| (125) |
ls = 1 - l(1 - s). A lover of none but servants is not a lover of a non-servant. Cf. 116. †3 |
Mr. De Morgan denotes ls and ls by L S, and L,S respectively, Formal Logic, p. 341. †4 and he has traced out the manner of forming the converse and negative of such functions in detail. The following table contains most of his results in my notation. Cf. ib., p. 343; see also 244. †5 For the converse of m, I write ɯ; and for that of n, u.
| x |
𝐊x |
mn
mn - (1-m)(1-n)
mn = (1-m)(1-n) |
uɯ
uɯ = (1-u)(1-ɯ)
uɯ = (1-u)(1-ɯ) |
 -x -x |
𝐊 -x -x |
(1-m)n = m(1-n)
(1-m)m
m(1-n) |
ɯ(1-u) = (1-ɯ)u
ɯ(1-u)
(1-m)n |
113. I shall term the operation by which w is changed to lw, backward involution. All the laws of this but one are the same as for ordinary involution, and the one exception is of that kind which is said to prove the rule. It is that whereas with ordinary involution we have,
(ls)w = l(sw);
in backward involution we have
that is, the things which are lovers to nothing but things that are servants to nothing but women are the things which are lovers of servants to nothing but women.
114. The other fundamental formulæ of backward involution are as follows:
| (127) |
l  sw = lw,sw, sw = lw,sw, |
or, the things which are lovers or servants to nothing but women are the things which are lovers to nothing but women and servants to nothing but women.
or, the things which are lovers to nothing but French violinists are the things that are lovers to nothing but Frenchmen and lovers to nothing but violinists. This is perhaps not quite axiomatic. It is proved as follows. By (125) and (30)
l(f,u) =  -l (1-f,u) = -l (1-f,u) =  -(l(1-f) -(l(1-f)  l(1-u)) l(1-u))
By (125), (13), and (7),
lf,lu =  -l(1-f), -l(1-f), -l(1-u) = -l(1-u) =  -(l(1-f) -(l(1-f)  l(1-u)). l(1-u)).
Finally, the binomial theorem holds with backward involution. For those persons who are lovers of nothing but Frenchmen and violinists consist first of those who are lovers of nothing but Frenchmen; second, of those who in some ways are lovers of nothing but Frenchmen and in all other ways of nothing but violinists, and finally of those who are lovers only of violinists. That is,
| (129) |
l(u  f) = lu f) = lu  Σpl-pu,pf Σpl-pu,pf  lf. lf. |
In order to retain the numerical coefficients, we must let {l} be the number of persons that one person is lover of. We can then write
l(u+f) = lu + {l}l-†𝟏u,†𝟏f+ (({l}·{l-𝟏})/𝟐)l-‡-𝟐u,‡𝟐f + etc.
115. We have also the following formula which combines the two involutions:
that is, the things which are lovers of nothing but what are servants of all women are the same as the things which are related to all women as lovers of nothing but their servants.
116. It is worth while to mention, in passing, a singular proposition derivable from (128). Since, by (124) and (125)
xy = (1-x)(1-y), An x of none but y's is a non-x of all non-y's; i.e., xy = -x-y. †1
and since
1-(u  f) = f) =  -(u -(u  f) = f) =  -u, -u, -f = (1-u),(1-f), -f = (1-u),(1-f),
(128) gives us,
(1-l)(1-u),(1-f) = (1-l)(1-u)  Σp(1-(l-p))(1-u), Σp(1-(l-p))(1-u),
(1-p)(1-f)  (1-l)(1-f). (1-l)(1-f).
This is, of course, as true for u and f as for (1-u) and (1-f). Making those substitutions, and taking the negative of both sides, we have, by (124)
| (131) |
l(u,f) = (lu),Π'p((l-p)u  pf),(lf), pf),(lf), |
or, the lovers of French violinists are those persons who, in reference to every mode of loving whatever, either in that way love some violinists or in some other way love some Frenchmen. This logical proposition is certainly not self-evident, and its practical importance is considerable. In a similar way, from (12) we obtain
| (132) |
(e,c)f = Π'p(e(f-p)  cp), cp), |
that is, to say that a person is both emperor and conqueror of the same Frenchman is the same as to say that, taking any class of Frenchmen whatever, this person is either an emperor of some one of this class, or conqueror of some one among the remaining Frenchmen.
117. The properties of zero and unity, with reference to backward involution, are easily derived from (125). I give them here in comparison with the corresponding formulæ for forward involution.
| (133) 0x = 1 |
x0= 1. |
| (134) q0 = 0 |
0r = 0, |
where q is the converse of an unlimited relative, and r is greater than zero.
| (135) 1x = x |
x1 = x. |
| (136) y1 = y |
1z = z, |
where y is infinitesimal, and z is individual. Otherwise, both vanish.
where s is less than unity and p is a limited relative.
118. In other respects the formulæ for the two involutions are not so analogous as might be supposed; and this is owing to the dissimilarity between individuals and infinitesimals. We have, it is true, if X' is an infinitesimal and X' an individual,
| (139) |
X,(y,z) = X,y,X,z |
like |
(y,z)X' = y X',z X'; |
| (140) |
X,y0 = X,,X,y |
" |
X',y0 = X',y X'; |
| (141) |
{X,} = 𝟏 |
" |
[X'] = 𝟏. |
We also have
But we have not X'y = X'y, and consequently we have not sw ⤙ sw, for this fails if there is anything which is not a servant at all, while the corresponding formula sw ⤙ sw only fails if there is not anything which is a woman. Now, it is much more often the case that there is something which is not x, than that there is not anything which is x. We have with the backward involution, as with the forward, Cf. (92), (93) and 332. †1 the formulæ
| (143) |
If x ⤙ y |
yz ⤙ xz; Cf. (92), (93) and 332. †1 |
| (144) |
If x ⤙ y |
zx ⤙ zy; Cf. (92), (93) and 332. †1 |
The former of these gives us
or, whatever is lover to nothing but what is servant to nothing but women Or: Whatever is a lover-of-a-servant to nothing but women . . . etc. †2 stands to nothing but a woman in the relation of lover of every servant of hers. The following formulæ can be proved without difficulty.
or, every lover of somebody who is servant to nothing but a woman stands to nothing but women in the relation of lover of nothing but a servant of them.
or, whatever stands to a woman in the relation of lover of nothing but a servant of hers is a lover of nothing but servants of women.
The differentials of functions involving backward involution are
| (148) |
𝐝nx = {n}n-𝟏x,𝐝x. |
| (149) |
𝐝xl = xl,𝐝x log.x. |
In regard to powers of  we have we have
| (150) |
x = =  x. x. |
Exponents with a dot may also be put upon either side of the letters which they affect.
119. The greater number of functions of x in this algebra may be put in the form
φx = Σp Σq pA pxq pBq.
For all such functions Taylor's and Maclaurin's theorems hold good in the form,
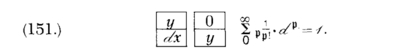
The symbol 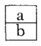 is used to denote that a is to be substituted for b in what follows. For the sake of perspicuity, I will write Maclaurin's theorem at length. is used to denote that a is to be substituted for b in what follows. For the sake of perspicuity, I will write Maclaurin's theorem at length.
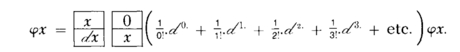
The proof of these theorems is very simple. The (p+q)th differential of pxq is the only one which does not vanish when x vanishes. This differential then becomes [p+q]!.p(𝐝x)q. It is plain, therefore, that the theorems hold when the coefficients pAq and pBq are 1. But the general development, by Maclaurin's theorem, of aφx or (φx)a is in a form which (112) reduces to identity. It is very likely that the application of these theorems is not confined within the limits to which I have restricted it. We may write these theorems in the form
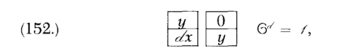
provided we assume that when the first differential is positive
 𝐝 = (𝟏/𝟎!)𝐝𝟎 + (𝟏/𝟏!)𝐝𝟏 + (𝟏/𝟐!)𝐝𝟐 + etc., 𝐝 = (𝟏/𝟎!)𝐝𝟎 + (𝟏/𝟏!)𝐝𝟏 + (𝟏/𝟐!)𝐝𝟐 + etc.,
but that when the first differential is negative this becomes by (111),
 𝐝 = 1 + 𝐝. 𝐝 = 1 + 𝐝.
120. As another illustration of the use which may be made of differentiation in logic, let us consider the following problem. In a certain institution all the officers (x) and also all their common friends (f) are privileged persons (y). How shall the class of privileged persons be reduced to a minimum? Here we have
y = x + fx,
𝐝y = 𝐝x + 𝐝fx = 𝐝x - fx,(1-f)𝐝x.
When y is at a minimum it is not diminished either by an increase or diminution of x. That is,
[𝐝y] ⤚ 0,
and when [x] is diminished by one,
[𝐝y] ⤙ 0 ,
When x is a minimum, then
|
[𝐝x-fx,(1-f)𝐝x] ⤚ |
0 [𝐝x-fx-I,(1-f)𝐝x] ⤙ 0 |
| (A) |
[𝐝x]-[fx,(1-f)𝐝x ⤚ |
0 [𝐝x]-[fx-I,(1-f)𝐝x] ⤙ 0 |
Now we have by (30)
fx,(1-f)𝐝x = fx-(0;0),(1-f)𝐝x.
Hence,
[fx] ⤙ [𝐝x]+(0;0).[(1-f)𝐝x].
[fx-𝟏] ⤚ [𝐝x]+(0;0).[(1-f)𝐝x].
But [0;0,] lies between the limits 0 and 1, and
We have, therefore,
[fx] ⤙ 1 + [(1-f)𝟏.] [fx-𝟏] ⤚ 𝟏.
This is the general solution of the problem. If the event of a person who may be an official in the institution being a friend of a second such person is independent of and equally probable with his being a friend of any third such person, and if we take p, or the whole class of such persons, for our universe, we have,
p = 1;
[fx,] = [fx]/[p] = ([f]/[p])[x],
[(1-f)𝐝x] = [1-f].[𝐝x] = ([p]-[f]).[𝐝x],
[fx,(1-f)𝐝x] = ([f])/[p])[x].([p]-[f]).[𝐝x]
Substituting these values in our equations marked (A) we get, by a little reduction,
[x] ⤚ (log([p]-[f]))/(log[p]-log[f]),
[x] ⤙ (log([p]-[f]))/(log[p]-log[f]) + 𝟏.
The same solution would be reached through quite a different road by applying the calculus of finite differences in the usual way.
Elementary Relatives Cf. 602ff. †1
121. By an elementary relative I mean one which signifies a relation which exists only between mutually exclusive pairs (or in the case of a conjugative term, triplets, or quartettes, etc.) of individuals, or else between pairs of classes in such a way that every individual of one class of the pair is in that relation to every individual of the other. If we suppose that in every school, every teacher teaches every pupil (a supposition which I shall tacitly make whenever in this paper I speak of a school), then pupil is an elementary relative. That every relative may be conceived of as a logical sum of elementary relatives is plain, from the fact that if a relation is sufficiently determined it can exist only between two individuals. Thus, a father is either father in the first ten years of the Christian era, or father in the second ten years, in the third ten years, in the first ten years, B. C., in the second ten years, or the third ten years, etc. Any one of these species of father is father for the first time or father for the second time, etc. Now such a relative as "father for the third time in the second decade of our era, of —" signifies a relation which can exist only between mutually exclusive pairs of individuals, and is therefore an elementary relative; and so the relative father may be resolved into a logical sum of elementary relatives.
122. The conception of a relative as resolvable into elementary relatives has the same sort of utility as the conception of a relative as resolvable into infinitesimals or of any term as resolvable into individuals.
123. Elementary simple relatives are connected together in systems of four. For if A:B be taken to denote the elementary relative which multiplied into B gives A, then this relation
existing as elementary, we have the four elementary relatives
An example of such a system is—colleague: teacher: pupil: schoolmate. In the same way, obviously, elementary conjugatives are in systems the number of members in which is (𝖓+1)𝖓+1 where 𝖓 is the number of correlates which the conjugative has. At present, I shall consider only the simple relatives.
124. The existence of an elementary relation supposes the existence of mutually exclusive pairs of classes. The first members of those pairs have something in common which discriminates them from the second members, and may therefore be united in one class, while the second members are united into a second class. Thus pupil is not an elementary relative unless there is an absolute distinction between those who teach and those who are taught. We have, therefore, two general absolute terms which are mutually exclusive, "body of teachers in a school," and "body of pupils in a school." These terms are general because it remains undetermined what school is referred to. I shall call the two mutually exclusive absolute terms which any system of elementary relatives supposes, the universal extremes of that system. There are certain characters in respect to the possession of which both members of any one of the pairs, between which there is a certain elementary relation, agree. Thus, the body of teachers and the body of pupils in any school agree in respect to the country and age in which they live, etc., etc. Such characters I term scalar characters for the system of elementary relatives to which they are so related; and the relatives written with a comma which signify the possession of such characters, I term scalars for the system. Thus, supposing French teachers have only French pupils and vice versa, the relative
f,
will be a scalar for the system "colleague: teacher: pupil: schoolmate." If r is an elementary relative for which s is a scalar,
125. Let c, t, p, s, denote the four elementary relatives of any system; such as colleague, teacher, pupil, schoolmate; and let a,, b,, c,, d,, be scalars for this system. Then any relative which is capable of expression in the form
a,c + b,t + c,p + d,s
I shall call a logical quaternion. Let such relatives be denoted by q, q', q'', etc. It is plain, then, from what has been said, that any relative may be regarded as resolvable into a logical sum of logical quaternions.
126. The multiplication of elementary relatives of the same system follows a very simple law. For if u and v be the two universal extremes of the system c, t, p, s, we may write
| c = u:u |
t = u:v |
p = v:u |
s = v:v, |
and then if w and w' are each either u or v, we have
| (155) |
(w':w) -w = 0. -w = 0. |
This gives us the following multiplication-table, where the multiplier is to be entered at the side of the table and the multiplicand at the top, and the product is found in the middle:
(156)
|
c |
t |
p |
s |
| c |
c |
t |
0 |
0 |
| t |
0 |
0 |
c |
t |
| p |
p |
s |
0 |
0 |
| s |
0 |
0 |
p |
s |
The sixteen propositions expressed by this table are in ordinary language as follows: See Lewis, Survey of Symbolic Logic, p. 103, for a symbolic and analytic account of some of these propositions.†1
The colleagues of the colleagues of any person are that person's colleagues;
The colleagues of the teachers of any person are that person's teachers;
There are no colleagues of any person's pupils;
There are no colleagues of any person's schoolmates;
There are no teachers of any person's colleagues;
There are no teachers of any person's teachers;
The teachers of the pupils of any person are that person's colleagues;
The teachers of the schoolmates of any person are that person's teachers;
The pupils of the colleagues of any person are that person's pupils;
The pupils of the teachers of any person are that person's schoolmates;
There are no pupils of any person's pupils;
There are no pupils of any person's schoolmates;
There are no schoolmates of any person's colleagues;
There are no schoolmates of any person's teachers;
The schoolmates of the pupils of any person are that person's pupils;
The schoolmates of the schoolmates of any person are that person's schoolmates.
This simplicity and regularity in the multiplication of elementary relatives must clearly enhance the utility of the conception of a relative as resolvable into a sum of logical quaternions.
127. It may sometimes be convenient to consider relatives each one of which is of the form
a,i + b,j + c,k + d,l + etc.
where a,, b,, c,, d,, etc. are scalars, and i, j, k, l, etc. are each of the form
m,u + n,v + o,w + etc.
where m,, n,, o,, etc. are scalars, and u, v, w, etc. are elementary relatives. In all such cases (155) Will give a multiplication-table for i, j, k, l, etc. For example, if we have three classes of individuals, u[1], u[2], u[3], which are related to one another in pairs, we may put
| u1:u1 = i |
u1:u2 = j |
u1:u3 = k |
| u2:u1 = l |
u2:u2 = m |
u2:u3 = n |
| u3:u1 = o |
u3:u2 = p |
u3:u3 = q |
and by (155) we get the multiplication-table
|
i |
j |
k |
l |
m |
n |
o |
p |
q |
| i |
i |
j |
k |
0 |
0 |
0 |
0 |
0 |
0 |
| j |
0 |
0 |
0 |
i |
j |
k |
0 |
0 |
0 |
| k |
0 |
0 |
0 |
0 |
0 |
0 |
i |
j |
k |
| l |
l |
m |
n |
0 |
0 |
0 |
0 |
0 |
0 |
| m |
0 |
0 |
0 |
l |
m |
n |
0 |
0 |
0 |
| n |
0 |
0 |
0 |
0 |
0 |
0 |
l |
m |
m |
| o |
o |
p |
q |
0 |
0 |
0 |
0 |
0 |
0 |
| p |
0 |
0 |
0 |
o |
p |
q |
0 |
0 |
0 |
| q |
0 |
0 |
0 |
0 |
0 |
0 |
o |
p |
q |
128. If we take
i = u1:u2 + u2:u3 + u3:u4,
j = u1:u3 + u2:u4,
k = 2.u1:u4,
we have
|
i |
j |
k |
| i |
j |
k |
0 |
| j |
k |
0 |
0 |
| k |
0 |
0 |
0 |
129. If we take
i = u1:u2 + u2:u3 + u3:u4 +u5:u6 + u7:u8,
j = u1:u3 +u2:u4,
k = 2.u1:u4,
l = u6:u8 + 𝖆.u5:u7 + 2𝖇.u1:u9 + u9:u4 + 𝖈.u5:u6,
m = u5:u8,
we have
|
i |
j |
k |
l |
m |
| i |
j |
k |
0 |
m |
0 |
| j |
k |
0 |
0 |
0 |
0 |
| k |
0 |
0 |
0 |
0 |
0 |
| l |
𝖆.m |
0 |
0 |
𝖇.k+
𝖈.m |
0 |
| m |
0 |
0 |
0 |
0 |
0 |
130. These multiplication-tables have been copied from Professor Peirce's monograph on Linear Associative Algebras. Linear Associative Algebras. By Benjamin Peirce. 4to, lithographed. Washington. 1870. [Published with notes and addenda by C. S. Peirce in The American Journal of Mathematics, vol. 4, pp. 97-229 (1881); see paper no. VIII of this volume.] †P1 I can assert, upon reasonable inductive evidence, that all such algebras can be interpreted on the principles of the present notation in the same way as those given above. In other words, all such algebras are complications and modifications of the algebra of (156). It is very likely that this is true of all algebras whatever. The algebra of (156), which is of such a fundamental character in reference to pure algebra and our logical notation, has been shown by Professor Peirce Ibid., (1612). †1 to be the algebra of Hamilton's quaternions. See Appendix to this volume. †2 In fact, if we put
where a, b, c, are scalars, then 1, i', j', k' are the four fundamental factors of quaternions, the multiplication-table of which is as follows:
|
1 |
i' |
j' |
k' |
| 1 |
1 |
i' |
j' |
k' |
| i' |
i' |
-1 |
k' |
-j' |
| j' |
j' |
-k' |
-1 |
i' |
| k' |
k' |
j' |
-i' |
-1 |
131. It is no part of my present purpose to consider the bearing upon the philosophy of space of this occurrence, in pure logic, of the algebra which expresses all the properties of space; but it is proper to point out that one method of working with this notation would be to transform the given logical expressions into the form of Hamilton's quaternions (after representing them as separated into elementary relatives), and then to make use of geometrical reasoning. The following formulæ will assist this procesS. Take the quaternion relative
q = xi + yj + zk + w l,
where x, y, z, and w are scalars. The conditions of q being a scalar, vector, etc. (that is, being denoted by an algebraic expression which denotes a scalar, a vector, etc., in geometry), are
| (157) |
Form of a scalar: x(i + l). |
| (158) |
Form of a vector: xi+y i+zk-x l. |
| (159) |
Form of a versor: |
| x/y((x/z)-1)-½i + y/x((x/z)-1)-½j + z/y((z/x)-1)-½k + y/z((z/x)-1)-½l. |
| (160) |
Form of zero: xi + x y j + (z/y)k + z l. |
| (161) |
Scalar of q: Sq = ½(x + w)(i + 1). |
| (162) |
Vector of q: Vq = ½(x-w)i + yj + zk + ½(w-x)l. |
| (163) |
Tensor of q: 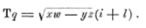 |
| (164) |
Conjugate of q: Kq = w i - yj - zk + x l. |
132. In order to exhibit the logical interpretations of these functions, let us consider a universe of married monogamists, in which husband and wife always have country, race, wealth, and virtue, in common. Let i denote "man that is —," j "husband of —," k "wife of —," and l "woman that is —"; x "negro that is —," y "rich person that is —," z "American that is —," and w "thief that is —." Then, q being defined as above, the q's of any class will consist of so many individuals of that class as are negro-men or women-thieves together with all persons who are rich husbands or American wives of persons of this class. Then, 2Sq denotes, by (160), By (161). †1 all the negroes and besides all the thieves, while Sq is the indefinite term which denotes half the negroes and thieves. Now, those persons who are self-q's of any class (that is, the q's of themselves among that class) are xi + w l; add to these their spouses and we have 2Sq. In general, let us term (j + k) the "correspondent of —." Then, the double scalar of any quaternion relative, q, is that relative which denotes all self-q's, and, besides, "all correspondents of self-q's of —." (Tq)2 denotes all persons belonging to pairs of corresponding self-q's minus all persons belonging to pairs of corresponding q's of each other.
133. As a very simple example of the application of geometry to the logic of relatives, we may take the following. Euclid's axiom concerning parallels corresponds to the quaternion principle that the square of a vector is a scalar. From this it follows, since by (157) yz + zk [?] is a vector, that the rich husbands and American wives of the rich husbands and American wives of any class of persons are wholly contained under that class, and can be described without any discrimination of sex. In point of fact, by (156), the rich husbands and American wiveS of the rich husbands and American wives of any class of persons, are the rich Americans of that class.
Lobatchewsky In his "New Elements of Geometry With a Complete Theory of Parallels," Gelehrte Schriften der Universität, Kasan, 1836-1838.†1 has shown that Euclid's axiom concerning parallels may be supposed to be false without invalidating the propositions of spherical trigonometry. In order, then, that corresponding propositions should hold good in logic, we need not resort to elementary relatives, but need only take S and V in such senses that every relative of the class considered should be capable of being regarded as a sum of a scalar and a vector, and that a scalar multiplied by a scalar should be a scalar, while the product of a scalar and a vector is a vector. Now, to fulfill these conditions we have only to take Sq as "self-q of," and Vq as "alio-q of" (q of another, that other being —), and q may be any relative whatever. For, "lover," for example, is divisible into self-lover and alio-lover; a self-lover of a self-benefactor of personS of any class is contained under that class, and neither the self-lover of an alio-benefactor of any persons nor the alio-lover of the self-benefactor of any persons are among those persons. Suppose, then, we take the formula of spherical trigonometry,
cos a = cos b cos c + cos A sin b sin c.
In quaternion form, this is,
| (165) |
S(p q) = (Sp)(Sq)+ S((Vp) (Vq)). |
Let p be "lover," and q be "benefactor." Then this reads, lovers of their own benefactors consist of self-lovers of self-benefactors together with alio-lovers of alio-benefactors of themselves. So the formula
sin b cos p b'= -sin a cos c cos p a' -sin c cos a cos p c'+ sin a sin c sin b cos p b,
where A', B', C', are the positive poles of the sides a, b, c, is in quaternions
| (166) |
V(p q) = (Vp)(Sq) + (Sp)(Vq) + V((Vp)(Vq)), |
and the logical interpretation of this is: lovers of benefactors of others consist of alio-lovers of self-benefactors, together with self-lovers of alio-benefactors, together with alio-lovers of alio-benefactors of others. It is a little striking that just as in the non-Euclidean or imaginary geometry of Lobatchewsky the axiom concerning parallels holds good only with the ultimate elements of space, so its logical equivalent holds good only for elementary relatives.
134. It follows from what has been said that for every proposition in geometry there is a proposition in the pure logic of relatives. But the method of working with logical algebra which is founded on this principle seems to be of little use. On the other hand, the fact promises to throw some light upon the philosophy of space. The researches of Lobatchewsky furnish no solution of the question concerning the apriority of space. For though he has shown that it is conceivable that space should have such properties that two lines might be in a plane and inclined to one another without ever meeting, however far produced, yet he has not shown that the facts implied in that supposition are inconsistent with supposing space to retain its present [Euclidean] nature and the properties only of the things in it to change. For example, in Lobatchewsky's geometry a star at an infinite distance has a finite parallax. But suppose space to have its present properties, and suppose that there were one point in the universe towards which anything being moved should expand, and away from which being moved should contract. Then this expansion and contraction might obey such a law that a star, the parallax of which was finite, should be at an infinite distance measured by the number of times a yard-stick must be laid down to measure off that distance. I have not seen Beltrami's investigations, ["Saggio di interpretazione della geometrica non-euclidea," Giorn. di Matem., 6, 1868.] but I understand that they do show that something of this sort is possible. Thus, it may be that, make what suppositions you will concerning phenomena, they can always be reconciled to our present geometry or be shown to involve implicit contradictions. If this is so—and whether it is or not is a completely open question—then the principles of geometry are necessary, and do not result from the specialities of any object cognized, but from the conditions of cognition in general. In speaking of the conditions of cognition, in general, I have in view no psychological conception, but only a distinction between principles which, if the facts should present a sufficient difficulty, I may always logically doubt, and principles which it can be shown cannot become open to doubt from any difficulty in my facts, as long as they continue to be supposed in all logical procedure.But, waiving this point, Lobatchewsky's conclusions do not positively overthrow the hypothesis that space is a priori. For he has only shown that a certain proposition, not usually believed to be axiomatical, is conceivably false. That people may be doubtful or even mistaken about a priori truth does not destroy all important practical distinction between the two kinds of necessity. It may be said that if Lobatchewsky's geometry is the true one, then space involves an arbitrary constant, which value cannot be given a priori. This may be; but it may be that the general properties of space, with the general fact that there is such a constant, are a priori, while the value of the constant is only empirically determined.It appears to me plain that no geometrical speculations will settle the philosophy of space, which is a logical question. If space is a priori, I believe that it is in some recondite way involved in the logic of relatives. †P1
§6. Properties of Particular Relative Terms Classification of Simple Relatives Cf. 225 and 585.†1
135. Any particular property which any class of relative terms may have may be stated in the form of an equation, and affords us another premiss for the solution of problems in which such terms occur. A good classification of relatives is, therefore, a great aid in the use of this notation, as the notation is also an aid in forming such a classification.
136. The first division of relatives is, of course, into simple relatives and conjugatives. The most fundamental divisions of simple relatives are based on the distinction between elementary relatives of the form (A:A), and those of the form (A:B). These are divisions in regard to the amount of opposition between relative and correlative.
a. Simple relatives are in this way primarily divisible into relatives all of whose elements are of the form (A:A) and those which contain elements of the form (A:B). The former express a mere agreement among things, the latter set one thing over against another, and in that sense express an opposition ({antikeisthai}); I shall therefore term the former concurrents, "As we speak of self-loving, etc., the former of these classes should be called self-relatives" — marginal note. †P1 and the latter opponents. The distinction appears in this notation as between relatives with a comma, such as (w,), and relatives without a comma, such as (w); and is evidently of the highest importance. The character which is signified by a concurrent relative is an absolute character, that signified by an opponent is a relative character, that is, one which cannot be prescinded from reference to a correlate.
b. The second division of simple relatives with reference to the amount of opposition between relative and correlative is into those whose elements may be arranged in collections of squares, each square like this,
| A:A |
A:B |
A:C |
| B:A |
B:B |
B:C |
| C:A |
C:B |
C:C |
and those whose elements cannot be so arranged. Cf. 230.†1 The former (examples of which are, "equal to —," "similar to —") may be called copulatives, "The idea of a copula is different. These should be called assimilative." — Marginal note. See 592. †P2 the latter non-copulatives. A copulative multiplied into itself gives itself. Professor Peirce calls letters having this property, idempotents. Op. cit., §25; see also 593.†2 The present distinction is of course very important in pure algebra. All concurrents are copulatives.
c. Third, relatives are divisible into those which for every element of the form (A:B) have another of the form (B:A), and those which want this symmetry. This is the old division into equiparants "If such reciprocation is admissible but not necessary they may be called reciprocal."—Marginal note.†P1 and disquiparants, "Quædam sunt relatione equiparantiæ, quædam disquiparantiæ. Primæ sunt relationes similium nominum, secundæ relationes dissimilium nominum. Exemplum primi est quando idem nomen ponitur in recto et in obliquo, sicut simile simili est simile.... Exemplum secundi est quando unum nomen ponitur in recto sed aliud in obliquo, sicut pater est filii pater et non oportet quod sit patris pater." Ockham Quodlibetum 6, qu. 20. See also his Summa Logices, pars 1, cap. 52. "Relativa equiparantiæ: quæ sunt synonyma cum suis correlativis.... Relativa diquiparantiæ: quæ non sunt synonyma cum suis correlativis." Pschlacher in Petr. Hisp. The same definitions substantially may be found in many late mediæval logics. †P2 or in Professor De Morgan's language, convertible and inconvertible relatives. Formal Logic, p. 345†1 Equiparants are their own correlatives. All copulatives are equiparant.
d. Fourth, simple relatives are divisible into those which contain elements of the form (A:A) and those which do not. The former express relations such as a thing may have to itself, the latter (as cousin of —, hater of —) relations which nothing can have to itself. The former may be termed self-relatives, "Instead of self-relatives, better concurrents."—Marginal note.†P3 the latter alio-relatives. All copulatives are self-relatives.
e. The fifth division is into relatives some power (i.e. repeated product) of which contains "Insert 'only' between contains and 'elements'; for 'non-cyclic' substitute 'acyclic.'" — Marginal note. †P4 elements of the form (A:A), and those of which this is not true. Cf. 233.†2 The former I term cyclic, the latter non-cyclic "Insert 'only' between contains and 'elements'; for 'non-cyclic' substitute 'acyclic.'" — Marginal note. †P5 relatives. As an example of the former, take
(A:B)  (B:A) (B:A)  (C:D) (C:D)  (D:E) (D:E)  (E:C). (E:C).
The product of this into itself is
(A:A)  (B:B) (B:B)  (C:E) (C:E)  (D:C) (D:C)  (E:D). (E:D).
The third power is
(A:B)  (B:A) (B:A)  (C:C) (C:C)  (D:D) (D:D)  (E:E). (E:E).
The fourth power is
(A:A)  (B:B) (B:B)  (C:D) (C:D)  (D:E) (D:E)  (E:C). (E:C).
The fifth power is
(A:B)  (B:A) (B:A)  (C:E) (C:E)  (D:C) (D:C)  (E:D). (E:D).
The sixth power is
(A:A)  (B:B) (B:B)  (C:C) (C:C)  (D:D) (D:D)  (E:E). (E:E).
where all the terms are of the form (A:A). Such relatives, as cousin of —, are cyclic. All equiparants are cyclic.
f. The sixth division is into relatives no power of which is zero, and relatives some power of which is zero. The former may be termed inexhaustible, the latter exhaustible. An example of the former is "spouse of —," of the latter, "husband of —." All cyclics are inexhaustible.
g. Seventh, simple relatives may be divided into those whose products into themselves are not zero, and those whose products into themselves are zero. The former may be termed repeating, the latter, non-repeating relatives. All inexhaustible relatives are repeating.
h. Repeating relatives may be divided (after De Morgan) into those whose products into themselves are contained under themselves, and those of which this is not true. The former are well named by De Morgan Op. cit., p. 346. †1 transitive, the latter intransitive. All transitives are inexhaustible; all copulatives are transitive; and all transitive equiparants are copulative. The class of transitive equiparants has a character, that of being self-relatives, not involved in the definitions of the terms. For if R is transitive then aRb.bRc ⤙ aRc; if R is also equiparant then aRb.bRa is true and aRa is a necessary consequent.†2
i. Transitives are further divisible into those whose products by themselves are equal to themselves, and those whose products by themselves are less than themselves; the former may be termed continuous, "Should be called concatenated" — marginal note.†P1 the latter discontinuous. An example of the second is found in the pure mathematics of a continuum, where if a is greater than b it is greater than something greater than b; and as long as a and b are not of the same magnitude, an intervening magnitude always exists. All concurrents are continuous.
j. Intransitives may be divided into those the number of the powers (repeated products) of which not contained in the first is infinite, and those some power of which is contained in the first. The former may be called infinites, the latter finites. Infinite inexhaustibles are cyclic.
In addition to these, the old divisions of relations into relations of reason and real relations, of the latter into aptitudinal and actual, and of the last into extrinsic and intrinsic, are often useful. "Duplex est relatio: scilicet rationis et realis. Unde relatio rationis est quae fit per actum comparativum intellectus, ut sunt secundæ intentiones; sed relatio realis est duplex, scilicet aptitudinalis et actualis. Aptitudinalis est quæ non requirit terminum actu existere sed solum in aptitudine; cujusmodi sunt omnes propriæ passiones, omnes aptitudines, et omnes inclinationes; et tales sunt in illo prædicamento reductive in quo sunt illa quorum sunt propriæ passiones. Sed relatio actualis est duplex, scilicet, intrinsecus adveniens, et extrinsecus adveniens. Intrinsecus adveniens est quae necessario ponitur positis extremis in quacunque etiam distantia ponantur, ut similitudo, paternitas, equalitas. Extrinsecus adveniens est quæ necessario non ponitur, positis extremis, sed requiritur debita approximatio extremorum; cujusmodi sunt sex ultima praedicamenta, scilicet, actio, passio, quando, ubi, situs, et habitus." Tartaretus. †P1
"NOT"
137. We have already seen that "not," or "other than," is denoted by  -1. It is often more convenient to write it, n. The fundamental property of this relative has been given above (111). It is that, -1. It is often more convenient to write it, n. The fundamental property of this relative has been given above (111). It is that,
 -x = 1 - x. -x = 1 - x.
Two other properties are expressed by the principles of contradiction and excluded middle. They are,
x, -x = 0; Cf. 8 and 81 (25), (26.) †1 x -x = 0; Cf. 8 and 81 (25), (26.) †1 x   -x = 1. Cf. 8 and 81 (25), (26.) †1 -x = 1. Cf. 8 and 81 (25), (26.) †1
The following deduced properties are of frequent application:
| (167) |
 -(x,y) = -(x,y) =  -x -x   -y; These two together contain De Morgan's Theorem to the effect that the negative of a logical product is the logical sum of the negatives of its factors; and that the negative of a sum (z=not) is the product of the negatives of the summands. †2 -y; These two together contain De Morgan's Theorem to the effect that the negative of a logical product is the logical sum of the negatives of its factors; and that the negative of a sum (z=not) is the product of the negatives of the summands. †2 |
| (168) |
 -xy = -xy =  -xy -xy |
The former of these is the counterpart of the general formula, zx  y = zx,zy These two together contain De Morgan's Theorem to the effect that the negative of a logical product is the logical sum of the negatives of its factors; and that the negative of a sum (z=not) is the product of the negatives of the summands. †2, The latter enables us always to bring the exponent of the exponent of y = zx,zy These two together contain De Morgan's Theorem to the effect that the negative of a logical product is the logical sum of the negatives of its factors; and that the negative of a sum (z=not) is the product of the negatives of the summands. †2, The latter enables us always to bring the exponent of the exponent of  - down to the line, and make it a factor. By the former principle, objects not French violinists consist of objects not Frenchmen, together with objects not violinists; by the latter, individuals not servants of all women are the same as non-servants of some women. - down to the line, and make it a factor. By the former principle, objects not French violinists consist of objects not Frenchmen, together with objects not violinists; by the latter, individuals not servants of all women are the same as non-servants of some women.
Another singular property of  - is that, - is that,
If [x] > 1  -1x = 1. -1x = 1.
"Case of the Existence of —," and "Case of the Non-Existence of —."
138. That which first led me to seek for the present extension of Boole's logical notation was the consideration that as he left his algebra, neither hypothetical propositions nor particular propositions could be properly expressed. It is true that Boole was able to express hypothetical propositions in a way which answered some purposes perfectly. He could, for example, express the proposition, "Either the sun will shine, or the enterprise will be postponed," by letting x denote "the truth of the proposition that the sun will shine," and y "the truth of the proposition that the enterprise will be postponed"; and writing,
x  y = 1, y = 1,
or, with the invertible addition,
x + (1 - x),y = 1.
But if he had given four letters denoting the four terms, "sun," "what is about to shine," "the enterprise," and "what is about to be postponed," he could make no use of these to express his disjunctive proposition, but would be obliged to assume others. The imperfection of the algebra here was obvious. As for particular propositions, Boole could not accurately express them at all. He did undertake to express them and wrote
| Some Y's are X's: |
v,y = v,x; |
| Some Y's are not X's: |
v,y = v,(1-x). |
The letter v is here used, says Boole, for an "indefinite class symbol." Laws of Thought, p. 62. †1 This betrays a radical misapprehension of the nature of a particular proposition. To say that some Y's are X's, is not the same as saying that a logical species of Y's are X's. For the logical species need not be the name of anything existing. It is only a certain description of things fully expressed by a mere definition, and it is a question of fact whether such a thing really exist or not. St. Anselm wished to infer existence from a definition, but that argument has long been exploded. If, then, v is a mere logical species in general, there is not necessarily any such thing, and the equation means nothing. If it is to be a logical species, then, it is necessary to suppose in addition that it exists, and further that some v is y. In short, it is necessary to assume concerning it the truth of a proposition, which, being itself particular, presents the original difficulty in regard to its symbolical expression. Moreover, from
v,y = v,(1-x)
we can, according to algebraic principles, deduce successively
v,y = v - v,x
v,x = v - v,y = v,(1-y).
Now if the first equation means that some Y's are not X's, the last ought to mean that some X's are not Y's; for the algebraic forms are the same, and the question is, whether the algebraic forms are adequate to the expression of particulars. It would appear, therefore, that the inference from Some Y's are not X's to Some X's are not Y's, is good; but it is not so, in fact.
139. What is wanted, in order to express hypotheticals and particulars analytically, is a relative term which shall denote "case of the existence of —," or "what exists only if there is any —"; or else "case of the non-existence of —," or "what exists only if there is not —." When Boole's algebra is extended to relative terms, it is easy to see what these particular relatives must be. For suppose that having expressed the propositions "it thunders," and "it lightens," we wish to express the fact that "if it lightens, it thunders." Let
A = 0 and B = 0,
be equations meaning respectively, it lightens and it thunders. Then, if φx vanishes when x does not and vice versa, whatever x may be, the formula
φA ⤙ φB
expresses that if it lightens it thunders; for if it lightens, A vanishes; hence φA does not vanish, hence φB does not vanish, hence B vanishes, hence it thunders. It makes no difference what the function φ is, provided only it fulfills the condition mentioned. Now, 0x is such a function, vanishing when x does not, and not vanishing when x does. Zero, therefore, may be interpreted as denoting "that which exists if, and only if, there is not —." Then the equation
00 = 1
means, everything which exists, exists only if there is not anything which does not exist. So,
0x = 0
means that there is nothing which exists if, and only if, some x does not exist. The reason of this is that some x means some existing x.
"It lightens" and "it thunders" might have been expressed by equations in the forms
A = 1, B = 1.
In that case, in order to express that if it lightens it thunders, in the form
φA ⤙ φB,
it would only be necessary to find a function, φx, which should vanish unless x were 1, and should not vanish if x were 1. Such a function is 1x. We must therefore interpret 1 as "that which exists if, and only if, there is —," 1x as "that which exists if, and only if, there is nothing but x," and 1x as "that which exists if, and only if, there is some x." Then the equation
1x = 1,
means everything exists if, and only if, whatever x there is exists.
140. Every hypothetical proposition may be put into four equivalent forms, as follows:
If X, then Y.
If not Y, then not X.
Either not X or Y.
Not both X and not Y.
If the propositions X and Y are A = 1 and B = 1, these four forms are naturally expressed by
1A ⤙ 1B,
1(1-A) ⤙ 1(1-B), This should be 1(1-B) ⤙ 1(1-A) †1
1(1-A)  B = 1, B = 1,
1A, 1(1-B) = 0.
For 1x we may always substitute 0(1-x).
141. Particular propositions are expressed by the consideration that they are contradictory of universal propositions. Thus, as h,(1-b) = 0 means every horse is black, so 0h,(1-b) = 0 means that some horse is not black; and as h,b = 0 means that no horse is black, so 0h,b = 0 means that some horse is black. We may also write the particular affirmative 1(h,b) = 1, and the particular negative 1(h,nb) = 1.
142. Given the premisses, every horse is black, and every horse is an animal; required the conclusion. We have given
h ⤙ b;
h ⤙ a.
Commutatively multiplying, we get
h ⤙ a,b.
Then, by (92) or by (90),
| 0a,b ⤙ 0h, |
or |
1h ⤙ 1(a,b). |
Hence, by (40) or by (46),
| If h > 0 0a,b = 0, |
or |
1(a,b) = 1; |
or if there are any horses, some animals are black. I think it would be difficult to reach this conclusion, by Boole's method unmodified.
143. Particular propositions may also be expressed by means of the signs of inequality. Thus, some animals are horses, may be written
a,h > 0;
and the conclusion required in the above problem might have been obtained in thiS form, very easily, from the product of the premisses, by (1) and (21).
We shall presently see In 146. †1 that conditional and disjunctive propositions may also be expressed in a different way.
Conjugative Terms
144. The treatment of conjugative terms presents considerable difficulty, and would no doubt be greatly facilitated by algebraic devices. I have, however, studied this part of my notation but little.
A relative term cannot possibly be reduced to any combination of absolute terms, nor can a conjugative term be reduced to any combination of simple relatives; but a conjugative having more than two correlates can always be reduced to a combination of conjugatives of two correlates. Thus for "winner over of —, from —, to —," we may always substitute 𝐮, or "gainer of the advantage — to —," where the first correlate is itself to be another conjugative 𝐯, or "the advantage of winning over of — from —." Then we may write,
𝐰 = 𝐮 𝐯.
It is evident that in this way all conjugatives may be expressed as production of conjugatives of two correlates.
145. The interpretation of such combinations as 𝐛am, etc., is not very easy. When the conjugative and its first correlative can be taken together apart from the second correlative, as in (𝐛a)m and (𝐛a)m and (𝐛a)m and (𝐛a)m, there is no perplexity, because in such cases (𝐛a) or (𝐛a) is a simple relative. We have, therefore, only to call the betrayer to an enemy an inimical betrayer, when we have
(𝐛a)m = inimical betrayer of a man = betrayer of a man to an enemy of him,
(𝐛a)m = inimical betrayer of every man = betrayer of every man to an enemy of him.
And we have only to call the betrayer to every enemy an unbounded betrayer, in order to get
(𝐛a)m = unbounded betrayer of a man = betrayer of a man to every enemy of him,
(𝐛a)m = unbounded betrayer of every man = betrayer of every man to every enemy of him.
The two terms 𝐛am and 𝐛am are not quite so easily interpreted. Imagine a separated into infinitesimal relatives, A,,A,,,A,,,, etc., each of which is relative to but one individual which is m. Then, because all powers of A,,A,,,A,,,, etc., higher than the first, vanish, and because the number of such terms must be m, we have,
am = (A,  A,, A,,  A,,, A,,,  etc.)m = (A,m),(A,,m),(A,,,m), etc. etc.)m = (A,m),(A,,m),(A,,,m), etc.
or if M', M'', M''', etc., are the individual m's,
am = (A,M'),(A,,M''),(A,,,M'''), etc.
It is evident from this that 𝐛am is a betrayer to an A, of M', to an A,, of M'', to an A,,, of M''', etc., in short of all men to some enemy of them all. In order to interpret 𝐛am we have only to take the negative of it. This, by (124), is (1-𝐛)am, or a non-betrayer of all men to some enemy of them. Hence, 𝐛am, or that which is not this, is a betrayer of some man to each enemy of all men. To interpret 𝐛(am) we may put it in the form (1-𝐛)(1-a)m. This is "non-betrayer of a man to all non-enemies of all men." Now, a non-betrayer of some X to every Y, is the same as a betrayer of all X's to nothing but what is not Y; and the negative-of "non-enemy of all men," is "enemy of a man." Thus, 𝐛(am) is, "betrayer of all men to nothing but an enemy of a man." To interpret 𝐛am we may put it in the form (1-𝐛)(1-a)m, which is, "non-betrayer of a man to every non-enemy of him." This is a logical sum of terms, each of which is "non-betrayer of an individual man M to every non-enemy of M." Each of these terms is the same as "betrayer of M to nothing but an enemy of M." The sum of them, therefore, which is 𝐛am is "betrayer of some man to nothing but an enemy of him." In the same way it is obvious that 𝐛am is "betrayer of nothing but a man to nothing but an enemy of him." We have 𝐛am = 𝐛(1-a)(1-m) or "betrayer of all non-men to a non-enemy of all non-men." This is the same as "that which stands to something which is an enemy of nothing but a man in the relation of betrayer of nothing but men to what is not it." The interpretation of 𝐛am is obviously "betrayer of nothing but a man to an enemy of him." It is equally plain that 𝐛am is "betrayer of no man to anything but an enemy of him," and that 𝐛am is "betrayer of nothing but a man to every enemy of him." By putting 𝐛am in the form 𝐛(1-a)(1-m) we find that it denotes "betrayer of something besides a man to all things which are enemies of nothing but men." When an absolute term is put in place of a, the interpretations are obtained in the same way, with greater facility.
146. The sign of an operation is plainly a conjugative term. Thus, our commutative multiplication might be denoted by the conjugative
1,.
For we have
l,sw = 1,l,sw.
As conjugatives can all be reduced to conjugatives of two correlates, they might be expressed by an operative sign (for which a Hebrew letter might be used) put between the symbols for the two correlates. There would often be an advantage in doing this, owing to the intricacy of the usual notation for conjugatives. If these operational signs happened to agree in their properties with any of the signs of algebra, modifications of the algebraic signs might be used in place of Hebrew letters. For instance, if  were such that were such that
 x x yz = yz =  [13] [13] yz, The second half of this equation should be: 13xyz. †1 yz, The second half of this equation should be: 13xyz. †1
then, if we were to substitute for  the operational sign ר we have the operational sign ר we have
xר(yרz) = (xרy)רz,
which is the expression of the associative principle. So, if
 xy = xy =  yx yx
we may write,
xרy = yרx
which is the commutative principle. If both these equations held for any conjugative, we might conveniently express it by a modified sign +. For example, let us consider the conjugative "what is denoted by a term which either denotes — or else —." For this, the above principles obviously hold, and we may naturally denote it by  . Then, if p denotes Protestantism, r Romanism, and f what is false, . Then, if p denotes Protestantism, r Romanism, and f what is false,
p  r ⤙ f r ⤙ f
means either all Protestantism or all Romanism is false. In this way it is plain that all hypothetical propositions may be expressed. Moreover, if we suppose any term as "man" (m) to be separated into its individuals, M', M'', M''', etc., then,
M'  M'' M''  M''' M'''  etc., etc.,
means "some man." This may very naturally be written
'm'
and this gives us an improved way of writing a particular proposition; for
'x' ⤙ y
seems a simpler way of writing "Some X is Y" than
0x,y = 0.
Converse
147. If we separate lover into its elementary relatives, take the reciprocal of each of these, that is, change it from
and sum these reciprocals, we obtain the relative loved by. There is no such operation as this in ordinary arithmetic, but if we suppose a science of discrete quantity in quaternion form (a science of equal intervals in space), the sum of the reciprocals of the units of such a quaternion will be the conjugate-quaternion. For this reason, I express the conjugative term "what is related in the way that to — is —, to the latter" by 𝐊. The fundamental equations upon which the properties of this term depend are
| (169) |
K K = 1. |
| (170) |
If x < yz then z ⤙ (𝐊y)x, |
| or |
1(x,y z) = 1(z,𝐊yx) |
| We have, also, |
|
| (171) |
𝐊Σ = Σ𝐊, |
| (172) |
𝐊Π = Π𝐊, |
where Π denotes the product in the reverse order. Other equations will be found in Mr. De Morgan's table, given above. In 112. †1
Conclusion
148. If the question is asked, What are the axiomatic principles of this branch of logic, not deducible from others? I reply that whatever rank is assigned to the laws of contradiction and excluded middle belongs equally to the interpretations of all the general equations given under the head of "Application of the Algebraic signs to Logic," together with those relating to backward involution, and the principles expressed by equations (95), (96), (122), (142), (156), (25), (26), (14), (15).
149. But these axioms are mere substitutes for definitions of the universal logical relations, and so far as these can be defined, all axioms may be dispensed with. The fundamental principles of formal logic are not properly axioms, but definitions and divisions; and the only facts which it contains relate to the identity of the conceptions resulting from those processes with certain familiar ones.
|
 b is to mean that a and b denote the same class—the same collection of individuals.
b is to mean that a and b denote the same class—the same collection of individuals. b denote all the individuals contained under a and b together. †2 The operation here performed will differ from arithmetical addition in two respects: first, that it has reference to identity, not to equality; and second, that what is common to a and b is not taken into account twice over, as it would be in arithmetic. The first of these differences, however, amounts to nothing, inasmuch as the sign of identity would indicate the distinction in which it is founded; and therefore we may say that
b denote all the individuals contained under a and b together. †2 The operation here performed will differ from arithmetical addition in two respects: first, that it has reference to identity, not to equality; and second, that what is common to a and b is not taken into account twice over, as it would be in arithmetic. The first of these differences, however, amounts to nothing, inasmuch as the sign of identity would indicate the distinction in which it is founded; and therefore we may say that b
b  a + b. †1
a + b. †1 a
a  a †2
a †2 , and which I shall call the process of logical addition, is both commutative and associative. That is to say
, and which I shall call the process of logical addition, is both commutative and associative. That is to say a. †2
a. †2 b),c
b),c  a,c
a,c  b,c
b,c c
c  (a
(a  c),(b
c),(b  c).
c). a'+x+y+o
a'+x+y+o b'+x+z+o
b'+x+z+o c'+y+z+o
c'+y+z+o b
b  a'+b'+x+y+z+o
a'+b'+x+y+z+o b),c
b),c  y+z+o.
y+z+o. y+o
y+o z+o
z+o b,c
b,c  y+z+o
y+z+o x+o
x+o c
c  c'+x+y+z+o.
c'+x+y+z+o. c) = a'+c'+x+y+z+o
c) = a'+c'+x+y+z+o c)
c)  b'+c'+x+y+z+o
b'+c'+x+y+z+o c),(b
c),(b  c)
c)  c'+x+y+z+o ∴ (9).
c'+x+y+z+o ∴ (9). be the sign of logical subtraction; so defined that
be the sign of logical subtraction; so defined that x
x  a
a a
a  b.
b. b is uninterpretable. †2 If then we denote the contradictory negative of a class by the letter which denotes the class itself, with a line above it, †P1 if we denote by v a wholly indeterminate class, and if we allow (0
b is uninterpretable. †2 If then we denote the contradictory negative of a class by the letter which denotes the class itself, with a line above it, †P1 if we denote by v a wholly indeterminate class, and if we allow (0  1) to be a wholly uninterpretable symbol, we have
1) to be a wholly uninterpretable symbol, we have b
b  v,a,b+a,b̄+[0
v,a,b+a,b̄+[0  1],ā,b †3
1],ā,b †3 x
x  x
x  x - x
x - x a
a a;b
a;b a,b+v,ā,b̄+(1;0)a,b̄ †3
a,b+v,ā,b̄+(1;0)a,b̄ †3 x;x
x;x  x:x. †4
x:x. †4 1-x
1-x  0:x. †5
0:x. †5 0
0 0:x
0:x  1.
1. a,x+b,(1-x) †2
a,x+b,(1-x) †2 i,x+j,(1-x). †P1
i,x+j,(1-x). †P1 φ(1),x + φ(0),(1-x)
φ(1),x + φ(0),(1-x) φ(1 and 1),x,y + φ(1 and 0),x,ȳ + φ(0 and 1),x̄,y + φ(0 and 0),x̄,ȳ.
φ(1 and 1),x,y + φ(1 and 0),x,ȳ + φ(0 and 1),x̄,y + φ(0 and 0),x̄,ȳ. (φ(1)
(φ(1) x̄),(φ(0)
x̄),(φ(0)  x) †P2
x) †P2 (φ(1 and 1)
(φ(1 and 1)  x̄
x̄  ȳ),(φ(1 and 0)
ȳ),(φ(1 and 0)  x̄,
x̄,  y),
y), x
x  ȳ),(φ(0 and 0)
ȳ),(φ(0 and 0)  x
x  y).
y). y, we have,
y, we have, y
y  (1
(1  1),x,y+(1
1),x,y+(1  0),x,ȳ+(0
0),x,ȳ+(0  1),x̄,y+(0
1),x̄,y+(0  0),x̄,ȳ.
0),x̄,ȳ. 1)
1)  v.
v. 0
0  1.
1. 1
1  (0
(0  1).
1). 0
0  0.
0. 1;1,x,y+1;0,x,ȳ+0;1,x̄,y+0;0,x̄,ȳ.
1;1,x,y+1;0,x,ȳ+0;1,x̄,y+0;0,x̄,ȳ. 1
1 (1;0)
(1;0) 0
0 v.
v. b) - b
b) - b  a
a b)
b)  b
b  a.
a. b the value of b cannot be obtained.
b the value of b cannot be obtained. a
a a.
a. x,φ(1),φ(0)+(1-x),φ(1),φ(0).
x,φ(1),φ(0)+(1-x),φ(1),φ(0). 0 when φx
0 when φx  0.
0. (1- φ(1)),(1-φ(0))
(1- φ(1)),(1-φ(0))  0
0 φ(1),φ(0)+φ(1),(1-φ(0)) + φ(0),(1-φ(1)).
φ(1),φ(0)+φ(1),(1-φ(0)) + φ(0),(1-φ(1)). φ(0)
φ(0)  φ(1),φ(0)+φ(1),(1-φ(0))+φ(0),(1-φ(1)).
φ(1),φ(0)+φ(1),(1-φ(0))+φ(0),(1-φ(1)). φ(0)
φ(0)  1 when φx
1 when φx  1.
1. b
b b) + (a,b).
b) + (a,b). days when it hails and thunders.
days when it hails and thunders. p,q = p qp=q pq.
p,q = p qp=q pq. Y[p]
Y[p]  X,Y
X,Y Z[q]
Z[q]  X,Z
X,Z Z[r]
Z[r]  X,Z.
X,Z. p',q';p'
p',q';p'  p',q';q'.
p',q';q'. p',q'+r'p',q̄'(p',q̄')+r'p̄',q̄'(p̄',q̄')
p',q'+r'p',q̄'(p',q̄')+r'p̄',q̄'(p̄',q̄') p',q'+r'p̄',q'(p̄',q')+r'p̄',q̄'(p',q')
p',q'+r'p̄',q'(p̄',q')+r'p̄',q̄'(p',q') p',q'+r'p̄',q̄'(p̄',q̄').
p',q'+r'p̄',q̄'(p̄',q̄'). r'p̄',q̄'
r'p̄',q̄'  ((x,ȳ,z)/(x̄,y,z̄+ȳ))
((x,ȳ,z)/(x̄,y,z̄+ȳ)) p'- p',q̄'
p'- p',q̄'  q'- q',p̄'
q'- q',p̄' q̄' - p',q̄'
q̄' - p',q̄'  p̄' - q',p̄'
p̄' - q',p̄' p' - p'q'q'
p' - p'q'q'  q̄'- q̄p̄'p̄'
q̄'- q̄p̄'p̄' q' - q'p'p'
q' - q'p'p'  p̄' - p̄'q̄'q̄'
p̄' - p̄'q̄'q̄' q̄'p̄'
q̄'p̄'  (x̄,y,z̄+x̄,ȳ,z+x,ȳ,z+x̄,ȳ,z̄)/(1 - x,y)
(x̄,y,z̄+x̄,ȳ,z+x,ȳ,z+x̄,ȳ,z̄)/(1 - x,y) p̄'q̄'
p̄'q̄'  (x̄,y,z̄+x̄,ȳ,z+x,ȳ,z+x̄,ȳ,z̄)/(1 - y,z)
(x̄,y,z̄+x̄,ȳ,z+x,ȳ,z+x̄,ȳ,z̄)/(1 - y,z) r;q
r;q  r+v,(1-q) because p is interpretable.
r+v,(1-q) because p is interpretable. the questions put to both witnesses,
the questions put to both witnesses, those which the first answers truly,
those which the first answers truly, those which the second answers truly,
those which the second answers truly, those wherein they disagree,
those wherein they disagree, those which both answer truly,
those which both answer truly, those which both answer falsely.
those which both answer falsely. p,q
p,q p̄,q̄
p̄,q̄ p
p  q - w
q - w  p̄
p̄  q̄ - w'.
q̄ - w'. q = p + q - w
q = p + q - w q̄ = p - p + 1 - q - w'.
q̄ = p - p + 1 - q - w'. w.
w. w'.
w'. i, a is the expression for some a. Boole cannot properly express some a.
i, a is the expression for some a. Boole cannot properly express some a.