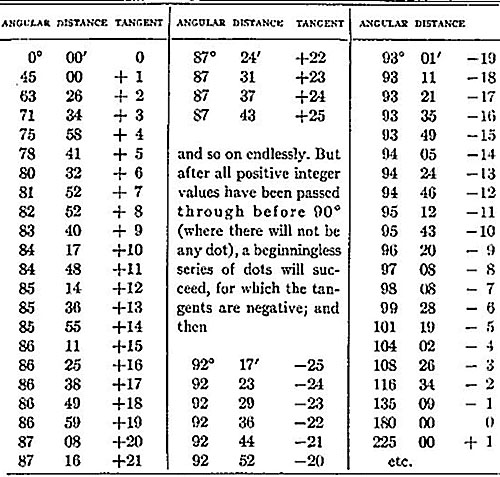
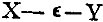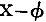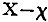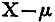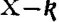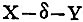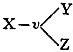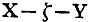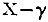Book 1: Logic and Mathematics (Unpublished Papers)
Preface †1
1. . . . Now what was the question of realism and nominalism? †2 I see no objection to defining it as the question of which is the best, the laws or the facts under those laws. It is true that it was not stated in this way. As stated, the question was whether universals, such as the Horse, the Ass, the Zebra, and so forth, were in re or in rerum natura. But that there is no great merit in this formulation of the question is shown by two facts; first, that many different answers were given to it, instead of merely yes and no, and second, that all the disputants divided the question into various parts. It was therefore a broad question and it is proper to look beyond the letter into the spirit of it. Most of those scholastics whose works are occasionally read today were matter-of-fact dualists; and when they used the phrase in re or in rerum natura in formulating the question, they took for granted something in regard to which other disputants, however confusedly, were at odds with them. For some of them regarded the universals as more real than the individuals. Therefore, the reality, or as I would say in order to avoid any begging of the question, the value or worth, not merely of the universals, but also that of the individuals was a part of the broad question. Finally, it was always agreed that there were other sorts of universals besides genera and species, and in using the word law, or regularity, we bring into prominence the kind of universals to which modern science pays most attention. Roughly speaking, the nominalists conceived the general element of cognition to be merely a convenience for understanding this and that fact and to amount to nothing except for cognition, while the realists, still more roughly speaking, looked upon the general, not only as the end and aim of knowledge, but also as the most important element of being. Such was and is the question. It is as pressing today as ever it was, Ernst Mach, †1 for example, holding that generality is a mere device for economising labor while Hegeler, †2 though he extols Mach to the skies, thinks he has said that man is immortal when he has only said that his influence survives him.
According to the nominalistic view, the only value which an idea has is to represent the fact, and therefore the only respect in which a system of ideas has more value than the sum of the values of the ideas of which it is composed is that it is compendious; while, according to the realistic view, this is more or less incorrect depending upon how far the realism be pushed.
Dr. [F.E.] Abbot in his Scientific Theism [1885] has so clearly and with such admirable simplicity shown that modern science is realistic that it is perhaps injudicious for me to attempt* to add anything upon the subject. Yet I shall try to put it into such a light that it may reflect some rays upon the worth or worthlessness of detached ideas. But I warn you that I shall not argue the question, but only indicate what my line of reasoning would be were I to enter upon it in detail.
The burden of proof is undoubtedly upon the realists, because the nominalistic hypothesis is the simpler. Dr. Carus †3 professes himself a realist and yet accuses me of inconsistency in admitting Ockham's razor although I am a realist, thus, implying that he himself does not accept it. †4 But this brocard, Entia non sunt multiplicanda praeter necessitatem, that is, a hypothesis ought not to introduce complications not requisite to explain the facts, this is not distinctively nominalistic; it is the very roadbed of science. Science ought to try the simplest hypothesis first, with little regard to its probability or improbability, although regard ought to be paid to its consonance with other hypotheses, already accepted. This, like all the logical propositions I shall enunciate, is not a mere private impression of mine: it is a mathematically necessary deduction from unimpeachable generalizations of universally admitted facts of observation. The generalizations are themselves allowed by all the world; but still they have been submitted to the minutest criticism before being employed as premisses. It appears therefore that in scientific method the nominalists are entirely right. Everybody ought to be a nominalist at first, and to continue in that opinion until he is driven out of it by the force majeure of irreconcilable facts. Still he ought to be all the time on the lookout for these facts, considering how many other powerful minds have found themselves compelled to come over to realism.
Nor has the wealth of thought that has been expended upon the defenses of nominalism especially by four great English philosophers who have engineered the works, I mean Ockham, Hobbes, Berkeley, and James Mill, by any means been wasted. It has on the contrary been most precious for the clear comprehension of logic and of metaphysics. But as for the average nominalist whom you meet in the streets, he reminds me of the blind spot on the retina, so wonderfully does he unconsciously smooth over his field of vision and omit facts that stare him in the face, while seeing all round them without perceiving any gap in his view of the world. That any man not demented should be a realist is something he cannot conceive.
My plan for defeating nominalism is not simple nor direct; but it seems to me sure to be decisive, and to afford no difficulties except the mathematical toil that it requires. For as soon as you have once mounted the vantage-ground of the logic of relatives, which is related to ordinary logic precisely as the geometry of three dimensions is to the geometry of points on a line, as soon as you have scaled this height, I say, you find that you command the whole citadel of nominalism, which must thereupon fall almost without another blow.
I am going to describe in general terms what this logic of relatives is, so far as it bears upon this great controversy. And in doing so I can at the same time, without lengthening the lecture by more than three or four minutes, make my account of this generalized logic illustrate some of [the] relative advantages and disadvantages of detached ideas and of systematic thought, by simply forming it into a narrative of how I myself became acquainted with that logic.
2. I came to the study of philosophy not for its teaching about God, Freedom, and Immortality, but intensely curious about Cosmology and Psychology. In the early sixties I was a passionate devotee of Kant, at least as regarded the Transcendental Analytic in the Critic of the Pure Reason. I believed more implicitly in the two tables of the Functions of Judgment and the Categories than if they had been brought down from Sinai. Hegel, so far as I knew him through a book by Vera †1 repelled me. Now Kant points out certain relations between the categories. I detected others; but these others, if they had any orderly relation to a system of conceptions, at all, belonged to a larger system than that of Kant's list. Here there was a problem to which I devoted three hours a day for two years, rising from it, at length, with the demonstrative certitude that there was something wrong about Kant's formal logic. Accordingly, I read every book I could lay hands upon on logic, and of course Kant's essay on the falsche Spitzfindigkeit der vier syllogistischen Figuren; †2 and here I detected a fallacy similar to that of the phlogistic chemists. For Kant argues that the fact that all syllogisms can be reduced to Barbara shows that they involve no logical principle that Barbara does not involve. A chemist might as well argue, that because water boiled with zinc dust evolves hydrogen, and the hydrogen does not come from the zinc, therefore water is a mere form of hydrogen. In short, Kant omits to inquire whether the very reasoning by which he reduces the indirect moods to Barbara may not itself introduce an additional logical principle. Pursuing this suggestion, I found that that was in truth the case, and I succeeded [in 1866] in demonstrating that the second and third figures each involved a special additional logical principle, both of which enter into the fourth figure. †3 Namely, the additional principle of the second figure is that by which we pass from judging that among dumb brutes no animal with a hand can be found, to judging that among animals with hands no dumb brute can be found; and the additional principle of the third figure is that by which we pass from judging that among human beings there are females to that of judging that among female animals there are human beings. Although I do not stop to give the proof, I assert that it is rigidly demonstrated that these are distinct principles of logic. Thus to find that the passage from one way of viewing a fact to another way of viewing the same fact should be a logical principle was naturally food for reflection. I remarked that while the circumstances under which propositions of the form No A is B and No B is A are true are identical, yet the circumstances under which such a pair of propositions indefinitely approximate to being true do not by any means indefinitely approximate toward being identical. For instance, the probability that a man taken at random will be a poet as great as Dante may be indefinitely near to zero; but it does not follow that the probability that a poet as great as Dante will be a man approximates to zero, at all. This reflection led me to inquire whether there might not be forms of probable reasoning analogous to the second and third figures of syllogism which were widely different from one another and from the first figure. Here, Aristotle's account of induction aided me; for Aristotle †1 makes induction to be a probable syllogism in the third figure.
3. I found that there was also a mode of probable reasoning in the second figure essentially different both from induction and from probable deduction. †2 This was plainly what is called reasoning from consequent to antecedent, and in many books is called adopting a hypothesis for the sake of the explanation it affords of known facts. It would be tedious to show how this discovery led to the thorough refutation of the third and most important of Kant's triads, and the confirmation of the doctrine that for the purposes of ordinary syllogism categorical propositions and conditional propositions, which Kant and his ignorant adherents call hypotheticals, are all one. †3 This led me to see that the relation between subject and predicate, or antecedent and consequent, is essentially the same as that between premiss and conclusion. †4 It was interesting to see how the combined result of all these improvements and some others to which I have not alluded was decidedly to consolidate that systematic or synthetic unity in the system of formal logic which occupied so large a place in Kant's thought. But though there was more unity than in Kant's system, still, as the subject stood, there was not as much as might be desired. Why should there be three principles of reasoning, and what have they to do with one another? This question, which was connected with other parts of my schedule of philosophical inquiry that need not be detailed, now came to the front. Even without Kant's categories, the recurrence of triads in logic was quite marked, and must be the croppings out of some fundamental conceptions. I now undertook to ascertain what the conceptions were. This search resulted in what I call my categories. I then †1 named them Quality, Relation, and Representation. But I was not then aware that undecomposable relations may necessarily require more subjects than two; for this reason Reaction is a better term. Moreover, I did not then know enough about language to see that to attempt to make the word representation serve for an idea so much more general than any it habitually carried, was injudicious. The word mediation would be better. Quality, reaction, and mediation will do. But for scientific terms, Firstness, Secondness, and Thirdness, are to be preferred as being entirely new words without any false associations whatever. How the conceptions are named makes, however, little difference. I will endeavor to convey to you some idea of the conceptions themselves. †2 It is to be remembered that they are excessively general ideas, so very uncommonly general that it is far from easy to get any but a vague apprehension of their meaning. . . .
4. [With regard to] my logical studies in 1867, various facts proved to me beyond a doubt that my scheme of formal logic was still incomplete. For one thing, I found it quite impossible to represent in syllogisms any course of reasoning in geometry, or even any reasoning in algebra, except in Boole's logical algebra. Moreover, I had found that Boole's algebra required enlargement to enable it to represent the ordinary syllogisms of the third figure; and though I had invented such an enlargement, it was evidently of a makeshift character, and there must be some other method springing out of the idea of the algebra itself. Besides, Boole's algebra suggested strongly its own imperfection. Putting these ideas together I discovered the logic of relatives. †1 I was not the first discoverer; but I thought I was, and had complemented Boole's algebra so far as to render it adequate to all reasoning about dyadic relations, before Professor De Morgan sent me his epoch-making memoir †2 in which he attacked the logic of relatives by another method in harmony with his own logical system. But the immense superiority of the Boolian method was apparent enough, and I shall never forget all there was of manliness and pathos in De Morgan's face when I pointed it out to him in 1870. I wondered whether when I was in my last days some young man would come and point out to me how much of my work must be superseded, and whether I should be able to take it with the same genuine candor. . . . †3
5. The great difference between the logic of relatives and ordinary logic is that the former regards the form of relation in all its generality and in its different possible species while the latter is tied down to the matter of the single special relation of similarity. The result is that every doctrine and conception of logic is wonderfully generalized, enriched, beautified, and completed in the logic of relatives.
Thus, the ordinary logic has a great deal to say about genera and species, or in our nineteenth century dialect, about classes. Now, a class is a set of objects comprising all that stand to one another in a special relation of similarity. But where ordinary logic talks of classes the logic of relatives talks of systems. A system is a set of objects comprising all that stand to one another in a group of connected relations. Induction according to ordinary logic rises from the contemplation of a sample of a class to that of the whole class; but according to the logic of relatives it rises from the contemplation of a fragment of a system to the envisagement of the complete system.
6. It is requisite that the reader should fully understand the relation of thought in itself to thinking, on the one hand, and to graphs, on the other hand. Those relations being once magisterially grasped, it will be seen that the graphs break to pieces all the really serious barriers, not only to the logical analysis of thought, but also to the digestion of a different lesson, by rendering literally visible before one's very eyes the operation of thinking in actu. In order that the fact should come to light that the method of graphs really accomplishes this marvelous result, it is first of all needful, or at least highly desirable, that the reader should have thoroughly assimilated, in all its parts, the truth that thinking always proceeds in the form of a dialogue — a dialogue between different phases of the ego — so that, being dialogical, it is essentially composed of signs, as its matter, in the sense in which a game of chess has the chessmen for its matter. Not that the particular signs employed are themselves the thought! Oh, no; no whit more than the skins of an onion are the onion. (About as much so, however.) One selfsame thought may be carried upon the vehicle of English, German, Greek, or Gaelic; in diagrams, or in equations, or in graphs: all these are but so many skins of the onion, its inessential accidents. Yet that the thought should have some possible expression for some possible interpreter, is the very being of its being. . . .
7. How many writers of our generation (if I must call names, in order to direct the reader to further acquaintance with a generally described character — let it be in this case the distinguished Husserl †1), after underscored protestations that their discourse shall be of logic exclusively and not by any means of psychology (almost all logicians protest that on file), forthwith become intent upon those elements of the process of thinking which seem to be special to a mind like that of the human race, as we find it, to too great neglect of those elements which must belong, as much to any one as to any other mode of embodying the same thought. It is one of the chief advantages of Existential Graphs, as a guide to Pragmaticism, that it holds up thought to our contemplation with the wrong side out, as it were; showing its construction in the barest and plainest manner, so that it [does not] seduce us into the bye-path of the distinctively English logicians (whether in that branch of it where the way is strewn, often in the most valuably suggestive works, such as Venn's Empirical Logic, with puerilities about words — and often not merely strewn with them but buried so deep in them, as by a great snowstorm, as to obstruct the reader's passage and render it fatiguing in the extreme, while the books of lesser inquirers, say Carveth Read, †1 Horace William Brindley Joseph, †2 and the last edition (greatly inferior to the first) of John Neville Keynes' Formal Logic, offer little reward for the labour of listening to their irrelevant baby-talk; or whether in the other branch of the same path where, as in the two Logics of Miss Constance Jones, †3 it seems to be forgotten that Latin Grammar does not furnish the only type even of Sud Germanic construction, which is itself a peculiarly specialized form of expression opposed in various particulars to the common ways of thinking of the great majority of mankind).
8. Nor does it lead us into the divarications of those who know no other logic than a "Natural History" of thought. As to this remark, I pray you, that "Natural History" is the term applied to the descriptive sciences of nature, that is to say, to sciences which describe different kinds of objects and classify them as well as they can while they still remain ignorant of their essences and of the ultimate agencies of their production, and which seek to explain the properties of those kinds by means of laws which another branch of science called "Natural Philosophy" has established. Thus a logic which is a natural history merely, has done no more than observe that certain conditions have been found attached to sound thought, but has no means of ascertaining whether the attachment be accidental or essential; and quite ignoring the circumstance that the very essence of thought lies open to our study; which study alone it is that men have always called "logic," or "dialectic."
Accordingly, when I say that Existential Graphs put before us moving pictures of thought, I mean of thought in its essence free from physiological and other accidents. . . .
9. The highest kind of symbol is one which signifies a growth, or self-development, of thought, and it is of that alone that a moving representation is possible; and accordingly, the central problem of logic is to say whether one given thought is truly, i.e., is adapted to be, a development of a given other or not. In other words, it is the critic of arguments. Accordingly, in my early papers I limited logic to the study of this problem. But since then, I have formed the opinion that the proper sphere of any science in a given stage of development of science is the study of such questions as one social group of men can properly devote their lives to answering †1; and it seems to me that in the present state of our knowledge of signs, the whole doctrine of the classification of signs and of what is essential to a given kind of sign, must be studied by one group of investigators. Therefore, I extend logic to embrace all the necessary principles of semeiotic, and I recognize a logic of icons, and a logic of indices, as well as a logic of symbols; and in this last I recognize three divisions: Stecheotic (or stoicheiology), which I formerly called Speculative Grammar; Critic, which I formerly called Logic; and Methodeutic, which I formerly called Speculative Rhetoric. †2
10. A fallacy is, for me, a supposititious thinking, a thinking that parades as a self-development of thought but is in fact begotten by some other sire than reason; and this has substantially been the usual view of modern logicians. For reasoning ceases to be Reason when it is no longer reasonable: thinking ceases to be Thought when true thought disowns it. A self-development of Thought takes the course that thinking will take that is sufficiently deliberate, and is not truly a self-development if it slips from being the thought of one object-thought to being the thought of another object-thought. It is, in the geological sense, a "fault" — an inconformability in the strata of thinking. The discussion of it does not appertain to pure logic, but to the application of logic to psychology. I only notice it here, as throwing a light upon what I do not mean by "Thought."
11. I trust by this time, Reader, that you are conscious of having some idea, which perhaps is not so dim as it seems to you to be, of what I mean by calling Existential Graphs a moving-picture of Thought. Please note that I have not called it a perfect picture. I am aware that it is not so: indeed, that is quite obvious. But I hold that it is considerably more nearly perfect than it seems to be at first glance, and quite sufficiently so to be called a portraiture of Thought.
Paper 1: A Boolian Algebra with One Constant †1
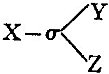
12. Every logical notation hitherto proposed has an unnecessary number of signs. It is by means of this excess that the calculus is rendered easy to use and that a symmetrical development of the subject is rendered possible; at the same time, the number of primary formulæ is thus greatly multiplied, those signifying facts of logic being very few in comparison with those which merely define the notation. I have thought that it might be curious to see the notation in which the number of signs should be reduced to a minimum; and with this view I have constructed the following. The apparatus of the Boolian calculus consists of the signs, =, > (not used by Boole, but necessary to express particular propositions) +, -, ×, 1, 0. In place of these seven signs, I propose to use a single one.
13. I begin with the description of the notation for conditional or "secondary" propositions. The different letters signify propositions. Any one proposition written down by itself is considered to be asserted. Thus,
A
means that the proposition A is true. Two propositions written in a pair are considered to be both denied. Thus,
A B
means that the propositions A and B are both false; and
A A
means that A is false. We may have pairs of pairs of propositions and higher complications. In this case we shall make use of commas, semicolons, colons, periods, and parentheses, just as [in] chemical notation, to separate pairs which are themselves paired. These punctuation marks can no more count for distinct signs of algebra, than the parentheses of the ordinary notation.
14. To express the proposition: "If S then P," first write
A
for this proposition. But the proposition is that a certain conceivable state of things is absent from the universe of possibility. Hence instead of A we write
B B
Then B expresses the possibility of S being true and P false. Since, therefore, SS denies S, it follows that (SS, P) expresses B. Hence we write
SS, P; SS, P. †1
15. Required to express the two premisses, "If S then M" and "if M then P." Let
A
be the two premisses. Let B be the denial of the first and C that of the second; then in place of A we write
B C
But we have just seen that B is (SS, M) and that C is (MM, P); accordingly we write
SS, M; MM, P.
16. All the formulae of the calculus may be obtained by development or elimination. The development or elimination having reference say to the letter X, two processes are required which may be called the erasure of the Xs and the erasure of the double Xs. The erasure of the Xs is performed as follows:
17. Erase all the Xs and fill up each blank with whatever it is paired with. But where there is a double X this cannot be done; in this case erase the whole pair of which the double X forms a part, and fill up the space with whatever it is paired with. Go on following these rules.
A pair of which both members are erased is to be considered as doubly erased. A pair of which either member is doubly erased is to be considered as only singly erased, without regard to the condition of the other member. Whatever is singly erased is to be replaced by the repetition of what it is paired with.
To erase the double Xs, repeat every X and then erase the Xs. †1
18. If φ be any expression, 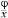 what it becomes after erasure of the Xs, and
what it becomes after erasure of the Xs, and 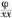 what it becomes after erasure of the double Xs, then
what it becomes after erasure of the double Xs, then
If φ be asserted, then
may be asserted.
19. The following are examples. Required to develop X in terms of X. Erasing the Xs the whole becomes erased, and
Erasing the double Xs, the whole becomes doubly erased and 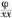 xx is erased. If φ, then
xx is erased. If φ, then
So that
X = xx, xx.
Required to eliminate X from (xx, x; a).
∴ φ = †1 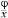
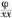 ,
, 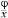
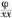 = aa, aa; aa, aa = aa.
= aa, aa; aa, aa = aa.
Required to eliminate X from (xa, a).
∴ φ †1 = aa, a; aa:aa, a; aa = aa, aa = a. †2
Required to develop (ax; b, xx:ab) according to X.
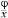 = a0; b, 00: ab = aa, aa; ab = a, ab = a †3
= a0; b, 00: ab = aa, aa; ab = a, ab = a †3
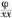 = a00; b, 0:ab = bb, bb; ab = b, ab = b †3
= a00; b, 0:ab = bb, bb; ab = b, ab = b †3
φ = 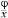 x,
x, 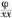 xx = ax; b, xx †3
xx = ax; b, xx †3
Required to eliminate M from (SS, M; MM, P).
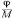 = SS, 0; 00, P = SS, SS; SS, SS = SS
= SS, 0; 00, P = SS, SS; SS, SS = SS
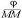 = SS, 00; 0, P = P, P; P, P = P
= SS, 00; 0, P = P, P; P, P = P
∴ SS, M; MM, P = †1 SS, P; SS, P
which is the syllogistic conclusion.
We may now take an example in categoricals. Given the premisses "There is something besides Ss and Ms," and "There is nothing besides Ms and Ps," to find the conclusion. As the combined premisses state the existence of a non-S non-M and the non-existence of an MP, †4 they are expressed by
SM, SM; MP.
To eliminate M, we have
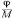 = S0, S0; 0P = SS, SS; PP = S, PP
= S0, S0; 0P = SS, SS; PP = S, PP
∴ 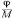
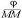 ,
, 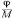
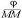 = †1 S, PP; 0:S, PP; 0 = †1 S, PP; S, PP: S, PP; S, PP = S, PP.
= †1 S, PP; 0:S, PP; 0 = †1 S, PP; S, PP: S, PP; S, PP = S, PP.
The conclusion therefore is that there is something which is not an S but is a P.
20. Of course, it is not maintained that this notation is convenient; but only that it shows for the first time the possibility of writing both universal and particular propositions with but one copula which serves at the same time as the only sign for compounding terms and which renders special signs for negation, for "what is" and for "nothing" unnecessary. It is true, that a 0 has been used, but it has only been used as the sign of an erasure. †2
Paper 2: The Essence of ReasoningP †1
§1. Some Historical Notes
21. . . . Logic having been written first in Greek had to be turned into Latin; and this was done for the most part by imitating the formation of each technical term. Thus, the Greek hypothesis, {hypothesis} was compounded of {hypo}, under and {tithenai}, to put. The preposition {hypo} was equivalent to the Latin sub — which is from the same root (being altered from sup), and {tithenai} was translated by ponere. Hence resulted suppositio. It is a very curious fact, by the way, that in this process it was always necessary to change the root. For, whether it be that there is something analogous to Grimm's law applying to meanings, as that applies to sounds, certain it is that the roots bear so uniformly different meanings that a different one must always be taken. Thus, the root of {tithenai} is the same as that of the Latin facere, so that hypothetical is the equivalent of sufficient, which widely diverges in meaning. Ponere is po-sinere, of which the root may be sa, to sow, to strew.
22. The earliest Latin work in which we find logical words so transferred from the Greek is supposed to be a treatise on Rhetoric (Ad Herennium) usually printed with the works of Cicero, but supposed to be written by one Cornificius, a little older than Cicero. Cicero himself made a number of words on that plan which are now very common, such as quantity and quality. †2
23. Apuleius, the author early in the second century of our era of the celebrated novel of the Golden Ass, wrote a treatise on logic which has somehow come to be arranged as the third book of his work De dogmate Platonis. The terminology of this treatise we may be pretty sure [Apuleius] did not invent, though it differs considerably from that of any other book which either preceded or for centuries followed it. That terminology has overridden other rival systems of translating the Greek words and has become largely ours. If the reader asks me what the quality was which lent it this staying power, he will be surprised at the answer. Namely, [Apuleius] had one of the most artificial, word-playing, fantastically and elaborately nonsensical styles that the Indo-European literatures can show. It sedulously cultivates every quality which writers upon style admonish us to avoid.
24. . . . Towards the end of the fifth century there was one Martianus Minneus Felix Capella, who wrote a work entitled the Nuptials of Philology and of Mercury. This Martianus Capella thought that beneath the stars there was nothing so beautiful nor so worthy of emulation as the style of Apuleius. He did his very best to outdo him; and in studying him became embued with his phraseology. Now in the book the Seven Liberal Arts are invited to the celebration of the Nuptials aforesaid, and each one entertains the company with the greatest good taste by talking shop for all she is worth. The consequence is that the book contains seven short treatises upon these disciplines, of which logic is one. Now the masters of the cathedral schools which at the fall of the Western Empire had to take the place of the old Roman schools found that in an age when one copy of one book and that not too large a one, was all that one school could commonly afford, the work of Capella was well adapted to their purpose. And thus it happened that for some centuries that was the only secular book that ordinary clerks had ever laid eyes upon. Thus, its borrowed terminology became traditional.
25. Anicius Manlius Severinus Boëtius (more commonly called Boëthius) was the author of a book which, whatever its merits and faults, was sincere and has in fact excited a degree of admiration such as has fallen to few works. He is most respectable as a thinker, a logician of positive strength, a man of great learning, a most estimable and sympathetic character, and the courageous supporter of calamities that touch every heart. . . .
26. Petrus Hispanus was a noble Portuguese who, having taken degrees in all the faculties in Paris, returned to Lisbon and was appointed head of that school which ultimately developed into the University of Coimbra. Subsequently, he was head physician to Pope Gregory X, who created him Cardinal; and he was crowned Pope, September 20, 1276. †1 He began his pontificate with promise of grandeur; but a part of his palace fell upon him and he died in consequence of his injuries on May 16, 1277. †1 This man, who had he survived would surely have been reckoned among the world's great men, was according to the tradition, the author of the Summulæ logicales, the regular textbook in logic almost to the very end of scholasticism. There are, it is true not very many printed editions subsequent to 1520; but over fifty editions having by that time been printed upon substantial linen paper, copies could always be procured in plenty. Manuscript copies were also current long after printing came in.
There is a Greek text of the book; it has been printed with the name of Michael Psellus attached to it. That name was a common one in Constantinople. Even if any MS. carries it, which has been denied, it does not prove that any particular Michael Psellus was the author; and the language, which is intermediate between Greek and a kind of Romaic, absolutely negatives the idea of its being written by any Michael Psellus known. It is full of Latinisms, and of reminiscences of Latin authors. The Latin text on the other hand bears on its first page conclusive evidence that the author did not know Greek. Namely, we there read: "Dicitur enim dyalectica a dya, quod est duo, et logos, quod est fermo vel lexis quod est ratio." Nevertheless, some writers, especially Prantl, †2 have believed the Greek text to be the original. Charles Thurot has written ably on the other side. When the reader comes across anything about "Byzantine" logic, what is meant is that this book is supposed to be the relic of a development of logic in Constantinople, which in my opinion is an unfounded fancy of Prantl's taken up by many writers without sufficient examination, and solely because Prantl has looked into more logical books of the middle ages than anybody else. I am very grateful to him for what he has read and published in a most convenient form; but I find myself compelled to dissent from his judgment very many times. A more slap-dash historian it would be impossible to conceive.
27. There is a synchronism between the different periods of medieval architecture, and the different periods of logic. The great dispute between the Nominalists and Realists took place while men were building the round-arched churches, and the elaboration finally attained corresponds to the intricate character of the opinions of the later disputants in that controversy. From that style of architecture we pass to the early pointed architecture with only plate-tracery. The simplicity of it is perfectly paralleled by the simplicity of the early logics of the thirteenth century. Among these simple writings, I reckon the commentaries of Averroes and of Albertus Magnus. I would add to them the writings of the great psychologist, St. Thomas Aquinas. For Thomistic Logic, I refer to Aquinas, †1 to Lambertus de Monte †2 whose work was approved by the Doctors of Cologne, to the highly esteemed Logic of the Doctors of Coimbra, †3 and to the modern manual of [Antoine] Bensa. †4
28. During the period of the Decorated Gothic, we have the writings of Duns Scotus, one of the greatest metaphysicians of all time, whose ideas are well worth careful study, and are remarkable for their subtilty, and their profound consideration of all aspects of the questions [of philosophy]. The logical upshot of the doctrine of Scotus is that real problems cannot be solved by metaphysics, but must be decided according to the evidence. As he was a theologian, that evidence was, for him, the dicta of the church. But the same system in the hands of a scientific man will lead to his insisting upon submitting everything to the test of observation. Especially, will he insist upon doing so as against so-called "experientialists," who, though they talk about experience as their guide, really reach the most important conclusions without any careful examination of experience. Whether their conclusions happen to be right or wrong, the Scotist will protest against the manner in which they are taken up. Scotus added a great deal to the language of logic. Of his invention is the word reality. For Scotistic logic I refer to Scotus, †1 Sirectus, †2 and Tartaretus. †3
29. Scotus died in 1308. After him William of Ockham, who died in 1347, took up once more the nominalistic opinion and this gained ground more and more. Logic now took on a very elaborate, but fanciful and in great measure senseless development; and finally became so big and so useless, that men must have dropped it, even if a new awakening of thought had not occurred. This was during the flamboyant period of architecture in France, the perpendicular in England. The Occamists made important additions to the terminology. For Occamistic Logic, I refer to Ockham's own elaborate treatise, †4 to the Summulæ of the Doctors of Mayence, to the commentaries of Bricot, †5 etc.
30. The new awakening consisted in the conviction that the classical authors had not been sufficiently studied. At the same time the reformation of the churches came. Logic once more became simple, and this time took on a rhetorical character. Ramus (Pierre de la Ramée), †6 Ludovicus Vives, †7 Laurentius Valla, †8 were the names of logicians who contributed a few things, but on the whole, rather important things to the tradition of logic.
31. Upon the heels of that movement came another, which has not yet expended itself, nor even quite completed its conquest of minds. It arose from the conviction that man had everything to learn from observation. The first great investigators in this line were Copernicus, Tycho Brahe, Kepler, Galileo, Harvey, and Gilbert. None of them seemed to have any interest at all in the general theory — and that for a simple reason; namely, they knew no way of inquiry but the way of experiment; and their lives were so many experiments in regard to the efficacity of the method of experimentation. The first great writer on the theory of Induction, Francis Bacon, was no scientific man. He had no turn that way, though he wished to have, and though he came to his death by a foolish experiment; and his judgments of scientific men were uniformly mistaken. The details of his theory were equally at fault; yet as long as he remains upon the ground of generalities, his ponderous charges are excellent. His Novum Organum, like several other great works of this period upon method, is marked by complete contempt for the Aristotelian analysis of reasoning, which nevertheless has kept the field, and, on the whole, held its ground. Still, Bacon made some distinct contributions to the traditional stock of logical ideas. . . .
32. The works we are now coming to are of less historical interest, precisely because they have to be taken seriously. Truly to paint the ground where we ourselves are standing is an impossible problem in historical perspective. . . .
33. The nominalistic wing of the Lockian party, much influenced by Hobbes and Ockham, made a philosophical development, chiefly psychological, but also logical. Among their names are Hartley, Berkeley, Hume, James Mill, John Stuart Mill, Bain. Bentham's Logic I must confess I do not remember to have seen. That of Mill, which appeared in 1843, contributed some phrases, which many persons adhere to passionately without reference to their meaning, sometimes seeming to attach no meaning to them, except the general one of a party-reveil. The present writer cares nothing about social matters, and knows not what such things mean. He examines logical questions as such and question by question. He perceives that many adherents of John Stuart Mill seem to be in a passion about something. But until they can calm themselves sufficiently, any scientific discussion of the questions, which perhaps they care little about, anyway, is impossible.
34. All the Occamistic school, from the Venerable Inceptor down, have been more or less politicians. John Stuart Mill was hypochondrically scrupulous. Nevertheless, every man of action is, must be, and ought to be, cunning, worldly, and dishonest, or what seems so to a man of pure science. When such men dispute, the dispute has some other object than the ascertainment of scientific truth. Men accomplish, roughly speaking, what they desire. Government may be ever so much more important than science; but only those men can advance science who desire simply to find out how things really are, without arrière-pensée.
35. Occamism is governed by a very judicious maxim of logic, called Ockham's razor. It runs thus: Entia non sunt multiplicanda præter necessitatem, that is, "Try the theory of fewest elements first; and only complicate it as such complication proves indispensible for the ascertainment of truth." It may seem, at the outset, that the more complicated theory is the more probable. Nevertheless, it is highly desirable to stop and carefully to examine the simpler theory, and not contenting oneself with concluding that it will not do, to note precisely what the nature of its shortcomings are. Realism can never establish itself except upon the basis of an ungrudging acceptance of that truth. The Occamists have followed out this rule in the most interesting manner, and have contributed much to human knowledge. Reasons will be given †1 for thinking that their simple theory will not answer; yet this in no wise detracts from their scientific merits, since the only satisfactory way of ascertaining the insufficiency of the theory was to push the application of it, just as they have done. But because the abandonment of the theory would imply the modification of their politics, they employ every means in their power to discredit and personally hamper those who reject it and to prevent the publication and circulation of works in which it is impartially examined. That is not the conduct of philosophers, however wise it may be from the point of view of statesmanship. . . .
36. As a logician [Leibniz] was a nominalist and leaned to the opinion of Raymond Lully, an absurdity here passed over as not worth mention. This very nominalism led Leibniz to an extraordinary metaphysical theory, his Monadology, of much interest. In regard to human knowledge, he put forth many ideas which had great influence, all of them rooted in nominalism, yet at the same time departing widely from the Occamistic spirit. Such were his tests of universality and necessity; and such was his principle of sufficient reason, which he regarded as one of the fundamental principles of logic. This principle is that whatever exists has a reason for existing, not a blind cause, but a reason. A reason is something essentially general, so that this seems to confer reality upon generals. Yet if realism be accepted, there is no need of any principle of sufficient reason. In that case, existing things do not need supporting reasons; for they are reasons, themselves. A great deal of the Leibnizian philosophy consists of attempts to annul the effect of nominalistic hypotheses. . . .
37. Immanuel Kant, who made a revolution in philosophy by his Critic of the Pure Reason, 1781, had great power as a logician. He unfortunately had the opinion that the traditional logic was perfect and that there was no room for any further development of it. †1 That opinion did not prevent his introducing a number of ideas which have indirectly more than directly affected the traditional logic.
The merits of German philosophers since Kant as logicians have in the opinion of the present writer been small, while their errors and vagaries have been incessant. †2 At any rate, they have had little or no effect upon the ordinary logic. . . .
§2. The Proposition
38. Very little of the traditional logic relates to the subject of the present section. St. Thomas Aquinas †3 divides the operations of the Understanding in reference to the logical character of their products into
Simple Apprehension,
Judgment, and
Ratiocination, or Reasoning.
Prantl declares †4 the commentary on the Perihermeneias in which this occurs not to be the work of Aquinas. But he does not explain how it could possibly happen that all the other books of the commentary should be genuine, as he admits they are, and this spurious. From the manner in which such books are written it is utterly inadmissible to suppose Aquinas passed over this book without comment. Such conduct would have excited a riot the noise of which would have reached our ears. If, then, the existing commentary is spurious, how could the genuine one have been lost? Thomas Aquinas was already an object of worship living. There was no school which adhered so religiously to the tenets of their master. Prantl himself complains that there is absolutely nothing in the works of Lambertus de Monte, and other Thomists except what St. Thomas had said. How could, then, all those schools be deceived into rejecting one of the works of their holy master, and taking in its place a writing that was not his? How is it that men of such learning as the doctors of Coimbra should get no wind of the substitution? Even Duns Scotus, writing directly after Aquinas, uses in his questions expressions which he probably derived from the book which Prantl suspects. Prantl gives no reason whatever for his rejection. He seems to think his judgment will be so commended by the comparison of it with manuscripts in other cases so entirely that he is placed quite above the necessity of giving reasons for his opinions. Similar ideas are apt to get possession of Germans.
39. Simple Apprehension produces concepts expressed by names or terms, "man," a state, suspended existence, the character of eating canned vacuum.
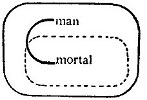
Judgment produces judgments, which are true or false, and are expressed by sentences, or propositions, as "Man is mortal," "some men may be insane."
Ratiocination or reasoning produces inferences or reasonings, which are expressed by argumentations, as, " I think, therefore I must exist," "Enoch, being a man, must have died; and since the Bible says he did not die, not everything in the Bible can be true."
40. A term names something but asserts nothing; a proposition asserts. Propositions differ in modality, which is the degree of positiveness of their assertion, as in maybe, is, must be. In another respect propositions are said to be assertory, problematic, and apodictic. The old statement †1 was that propositions were either modal or de inesse, i.e., assertoric. They may also be probable assertions; they may further be approximate and probable assertions, as "about 51 per cent of the births in any one year will be male." Propositions are divided into the Categorical and the Hypothetical. "Propositionum alia categorica alia hypothetica," †1 says the Summulæ. A categorical proposition is one whose immediate parts are terms; or as the Summulæ of the Mayence doctors say, †2 "cathegorica est illa quæ habet subiectum et prædicatum tanguam partes principales sui." A hypothetical proposition, better called by the Stoics †3 a composite proposition, is one which is composed of other propositions: "Propositio hypothetica est illa quæ habet duas propositiones cathegoricas tanquam partes principales sui." †4 The old, and less incorrect doctrine about compound propositions was that they were of three kinds, conditional, copulative, and disjunctive. †5 A conditional proposition is one whose members are joined by an if, or its equivalent: "Conditionalis est illa in qua coniunguntur duæ cathegoricæ per hanc coniunctionem, si." †6 That is, what is asserted is that in case one proposition, called the antecedent, is true, another proposition, called the consequent, is true. But how it may be in the opposite case in which the antecedent is not true is not stated. A copulative proposition is one in which the truth of every one of several propositions is affirmed. A disjunctive proposition is one in which the truth of some one of several propositions is affirmed. This enumeration is faulty because the conditional and disjunctive do not differ from one another in the same way in which both differ from the copulative proposition. For the conditional merely (or, at least, principally) asserts that unless one proposition is true another is true, that is, either the contrary of the former is true or the latter is true; and the disjunctive implies no more than that if the contradictions of all the alternatives but one be true, that one is true. Hence, either these two classes should be joined together, or we ought to include three other kinds of compound propositions, one which declares the repugnancy of two or more given propositions so that all cannot be true, one which declares the independence of one proposition of others so that it can be false although they are all true, and one which declares that there is a possibility that all of certain propositions are false. †1
41. The subject of a categorical proposition is that concerning which something is said, the predicate is that which is said of it. Most of the medieval logics teach that subject and predicate are the principal parts of the categorical proposition but that there is also a Copula which joins them together. . . . The Mayence doctors were quoted on this head, because Petrus Hispanus †2 makes the Subject, Predicate, and Copula to be all principal parts — one of the numerous evidences that the text is not a translation from the Greek, a language in which the copula may be dispensed with. Aristotle, however, in his treatise upon forms of propositions, the De interpretatione, †3 analyzes the categorical proposition into the noun, or nominative, and the verb.
42. Categorical propositions are said to be divided according to their Quantity, into the universal, the particular, the indefinite, and the singular. A universal proposition was said to be a proposition whose subject is a common term determined by a universal sign. A common term was defined as one which is adapted to being predicated of several things (aptus natus prædicari de pluribus †4). The universal signs are every, no, any, etc. A particular proposition was said to be a proposition whose subject is a common term determined by a particular sign. The particular signs are, some, etc. An indefinite proposition was said †5 to be one in which the subject is a common term without any sign, "ut homo currit." That unfortunate "indefinite" man has been running on now for so many centuries, it is fair he should have a rest and that we should revert to Aristotle's example, "Man is just." †6 A singular proposition was said to be one in which the subject is a singular term. A singular term was defined as "qui aptus natus est prædicari de uno solo," †7 that is, it is a proper noun. Kant and other modern logicians very rightly drop the indefinite propositions which merely arise from the imperfect expression of what is meant. Singular propositions are for the purposes of formal logic equivalent to universal ones.
43. Propositions were further distinguished into propositions per se and propositions per accidens. But this was a complicated doctrine, which Kant very conveniently replaced by the distinction between analytic, or explicatory, and synthetic, or ampliative, propositions. Namely, the question is what we are talking about. If we are saying that some imaginable kind of thing does or does not occur in the real world, or even in any well-established world of fiction (as when we ask whether Hamlet was mad or not), then the proposition is synthetic. But when we are merely saying that such and such a verbal combination does or does not represent anything that can find a place in any self-consistent supposition, then, we are either talking nonsense, as when we say, "A woolly horse would be a horse," or else, we are, as Kant says, †1 expressing a result of inward experimentation and observation, as when I say, "Probability essentially involves the supposition that certain general conditions are fulfilled many times and that in the long run a specific circumstance accompanies them in some definite proportion of the occurrences." If such a proposition is true and we substitute for the subject what that subject means, the proposition is reduced to an identical proposition, or in Kantian terminology an empty form of judgment. But the real sense of it lies in its being only just now seen that such is the meaning of the subject, that subject having hitherto been obscurely apprehended.
44. Categorical propositions are further divided into affirmative and negative propositions. A negative is one which has the particle of exclusion, not, or other than attached to the copula. There is a confusing distinction between a negative proposition and an infinite, that is, an indefinite one. The former is like homo non est equis, the latter like homo est non equis. That is the negative does not imply the existence of the subject, while the affirmative does imply this. But this arrangement, as will be shown in another chapter, †2 greatly complicates the description of correct reasonings. For analytical propositions, though affirmative, cannot, as analytical, assert the real existence of anything. †1
45. Ratiocination is defined by St. Thomas †2 as the operation by which reason proceeds from the known to the unknown. Inferences are of two kinds: the necessary and the probable. There are in either case (such is the traditional opinion which will be modified in this work †3) certain propositions called premisses laid down and granted; and these render another proposition, called the conclusion either necessary or probable, as the case may be. The conclusion is sometimes said to be collected from the premisses. It is also said to follow from them. The proposition that from such premisses such a conclusion follows, that is, is rendered necessary or probable, is called the logical rule, dictum, law, or principle. A necessary inference from a single premiss is called an immediate inference, from two premisses a syllogism, from more than two a sorites. The massing of a number of premisses into one conjunctive proposition, which, in general consonance with the doctrine of immediate inference, might be considered as the inference of the conjunctive proposition from its members, though it is not so conceived traditionally, is conveniently called by Whewell †4 a colligation. It is plain that colligation is half the battle in ratiocination. †5
It may be mentioned that Scotus (Duns, of course, for Scotus Erigena was not a scholastic) and the later scholastics usually dealt, not with the Syllogism, but with an inferential form called a consequence. The consequence has only one expressed premiss, called the antecedent; its conclusion is called the consequent; and the proposition which asserts that in case the antecedent be true, the consequent is true, is called the consequence. . . .
46. Logic ought, for the realization of its germinal idea, to be l'art de penser. L'art de penser! What a sublime conception. A school to which an age can turn and here learn the most efficient method of solving its theoretical problems! Such is the idea of logic; but it manifestly asks that the logician should be head and shoulders above his age. That is not at all impossible. There are such men by the dozen in every age. Unfortunately, that is not enough. The man must not only live in realms of thought far removed from that of his fellow-citizens, and really be vastly their intellectual superior, but he must also be recognized as such; and that is a combination of events which hardly ever has happened. Aristotle, alone, by the extraordinary chance of adding to his vast powers, inherited wealth, and the close friendship of two kings the most powerful in the world, and both of them, men of gigantic intellect, came near to that ideal. That logic should really teach an age to think must be confessed impracticable. Let it aspire in each age to register the highest method of thinking to which that age actually attains, and it will be doing all that can be expected. This calls for the best minds. But in few ages has even this been done. The logicians instead of generally riding on the crest of the thought-wave, have, three-quarters waterlogged, drifted wherever the motion of thought was least. . . .
§3 The Nature of Inference
47. We now come to the proper subject of this chapter. What is the nature of inference? What says the traditional syllogism? That an inference consists of a colligation of propositions which if true render certain or probable another collected proposition. If, to get to the bottom of the matter, we ask what is the nature of a proposition, traditional logic tells us, that it consists of terms — two terms, usually connected together by another kind of sign, a copula.
This is tolerably explicit, and, so far, good.
48. The next question, in order, which we put to the traditional logic, is, how do you know that all that is true? to divide the question, tell us, first, how you know that that analysis of the nature of assertion is correct.
To this, the traditional logic has not one traditional word to say. It is perfectly plain, however, that the reason it thinks so, is that that seems a satisfactory analysis of a sentence. So it is of the majority of sentences in the Greek, Latin, English, German, French, Italian, Spanish, languages — in short, in the Indo-European languages; and European grammarians, true children of Procrustes, manage to exhibit sentences in other languages forced into the same formula. †P1 But outside of that family of languages which bears somewhat the same relation to language in general as the phanerogams do to all plants, or the vertebrates to all animals — while there are of course proper names — it seems to me that general terms, in the logical sense, do not exist. †1 That the analysis of the proposition into subject and predicate represents tolerably the way we, Arians, think, I grant; but I deny that it is the only way to think. It is not even the clearest way nor the most effective way.
49. There appear to be very many languages in which the copula is quite needless. In the Old Egyptian language, which seems to come within earshot of the origin of speech, the most explicit expression of the copula is by means of a word, really the relative pronoun, which. Now to one who regards a sentence from the Indo-European point of view, it is a puzzle how "which" can possibly serve the purpose in place of "is." Yet nothing is more natural. †2 The fact that hieroglyphics came so easy to the Egyptians shows how their thought is pictorial. . . . [e.g.] "Aahmes what we write of is a soldier which what we write of is overthrown," means "Aahmes the soldier is overthrown." Are you on the whole quite sure that this is not the most effective way of analyzing the meaning of a proposition?
50. †3 Take, now, the other part of the question, namely, supposing the nature of assertion to be understood, what is the relation of inference to assertion, according to the traditional logic? Here we find a marked difference between the view taken down to A. D. 1300 or 1325 and the view which then gradually gained ground and became universal considerably before A. D. 1600, and remained so until long after A. D. 1800. After 250 years of contest in which it was always gaining ground, it remained for 250 years more in unchallenged possession of the field. The opinion referred to is nominalism. Ockham revived it. By the time the universities were reformed in the sixteenth century, it had gained a complete victory. Descartes, Leibniz, Locke, Hume, and Kant, the great landmarks of philosophical history, were all pronounced nominalists. Hegel first advocated realism; and Hegel unfortunately was about at the average degree of German correctness in logic. The author of the present treatise is a Scotistic realist. He entirely approved the brief statement of Dr. F. E. Abbott in his Scientific Theism that Realism is implied in modern science. In calling himself a Scotist, the writer does not mean that he is going back to the general views of 600 years back; he merely means that the point of metaphysics upon which Scotus chiefly insisted and which has since passed out of mind, is a very important point, inseparably bound up with the most important point to be insisted upon today. The author might with more reason, call himself a Hegelian; but that would be to appear to place himself among a known band of thinkers to which he does not in fact at all belong, although he is strongly drawn to them.
51. How, then, does Kant regard the apodictic inference? He holds that the conclusion is thought in the premisses although indistinctly. That that is Kant's view could be shown in a few words. But let us rather listen to his general tone in talking of reasoning. In the Critic of The Pure Reason, Transcendental Dialectic, Introduction, Section II, Subsection B, [A303, B359] he speaks of the logical employment of the Reason, as follows:
"A distinction is usual between things known immediately and things merely inferred. That in a figure bounded by three straight lines, there are three angles is known immediately; that the sum of these angles equals two right angles is a thing inferred. [When Kant wrote this no step in the modern revival of graphical geometry had been made. That three rays in a plane have three intersections, which, without any two rays coinciding, may reduce to one, is a theorem of graphics. But Kant confounds this proposition with another, namely, that if three lines, straight or not, enclose a space on a surface, those three lines must have at least three intersections. This is a corollary from the Census theorem of topology. That the sum of the three angles of the triangle equals two right angles, depends, as Lambert had clearly explained, before Kant wrote, upon a particular system of measurement which, however much it may be recommended by what we observe in nature, is not the only admissible system of measurement. Thus, what Kant says is immediately known, is fairly demonstrable; but what he says is demonstrable, is not so. This is not merely true in this case, but would be true of any example which Kant would feel to be a good one. It casts suspicion, at once, upon what he has to say, which has been the result of his generalizations of such examples]. Having an incessant need of inferring we become so accustomed to it, that at last the distinction spoken of escapes us. Even so called deceptions of the senses, where evidently it is the inferences that are at fault, we take for immediate perceptions. In every inference, there is one initial proposition, another, the consequent, which is drawn from it, and finally there is the consequence, or proposition according to which the truth of the consequent invariably accompanies the truth of the antecedent. [This is the doctrine of consequentia which is so extensively employed by philosophers of the fourteenth and fifteenth centuries.] If the concluded judgment is so contained in the initial judgment, that it can be derived without the intervention of any third idea, the consequence is called immediate. [This well-known term Kant would find in Wolff.] I would rather term it an Understanding-consequence. [This Kant seems to think an original idea, but that such a consequence was not an argument was the established doctrine.] But in case, besides the knowledge assigned as reason, still another judgment be needful, in order to draw the conclusion, the inference is called a Reason-inference. In the proposition "All men are mortal" is contained the propositions, "Some men are mortal," "Some mortals are men," "No immortal is a man." These, therefore, follow immediately from that. On the other hand, the proposition "All savans are mortal" is not contained in our assumed judgment (which does not contain the notion of savan), so that this proposition cannot be deduced from that other without a mediating judgment." [This is a slipshod analysis. Kant, out of his well-founded contempt for the scholastic method of trying to answer real questions by drawing distinctions, was led virtually to put the stamp of his condemnation upon all accurate thought. "Subtleties," he often says, "may sharpen the wits, but they are of no use at all." †P1 That was a very unfortunate opinion, which encouraged the down-at-the-heels, slouchy sort of logic to which Germans were prone enough and which has disgraced that country. To return to the present case, why does Kant consider only one kind of enthymeme and not another? Suppose the consequence to be the following — which represents an argument actually used by Kant against Boscovich —
All particles are bodies;
Ergo, All particles are extended.
Will Kant tell us there is any idea contained in this consequent not contained in its antecedent? Not so: he himself says, †1 "I need not go beyond the notion connected with the noun body to find that extension belongs to it." Will he, then, say that the consequence is no argument? It is put forward as such by himself; and such a doctrine would be a novelty in the traditional logic, with which he professes himself eminently satisfied, which were it involved in his doctrine, he certainly ought to have called attention to. But this example shows that in Kant's opinion the conclusion of a complete and perfect argumentation is implicitly contained in its premisses.]
52. "With the explanation of synthetical Knowledge," says Kant [Analytic of Principles, Chapter 2, Section 2, [A154, B193] of the highest principles of all synthetical judgments]," general logic has absolutely nothing to do." The reason is obvious. Reasoning, according to the doctrine of that work, is regulated entirely by the principle of contradiction, which is the principle of analytical thought. The one law of demonstrative reasoning is that nothing must be said in the conclusion which is not implied in the premisses, that is, nothing must be said in the conclusion, not actually thought in the premisses, though not so clearly and consciously. †P1 The proposition that that is actually thought, though somewhat unconsciously, which is implicitly contained in what is thought, is absurd enough; but it is a psychological absurdity which may perhaps be passed over in logic. If that be true, nobody can tell by the most attentive introspection, what he thinks. For it will not be maintained that by carefully considering the few and simple premisses of the theory of numbers — by just contemplating these propositions ever so nicely — one could even discover the truth of Fermat's theorems. It would be impossible to adduce a single instance of the discovery of anything deserving the name of a mathematical theorem by any such means. Every mathematical discoverer knows very well that that is no way to succeed. If the implied proposition be thought, it is thought in some cryptic sense, and it in no wise tells us how it is that inference is performed, to say that in such sense the conclusion is thought as soon as the premisses are given. The distinction between analytical and synthetical judgments represents this conception of reasoning. The distinction may approximate to a just and valuable distinction; but it cannot be accepted as accurately defined. . . .
53. †1 A belief is a habit; but it is a habit of which we are conscious. The actual calling to mind of the substance of a belief, not as personal to ourselves, but as holding good, or true, is a judgment. An inference is a passage from one belief to another; but not every such passage is an inference. If noticing my ink is bluish, I cast my eye out of the window and my mind being awakened to color remark particularly a poppy, that is no inference. Or if without casting my eye out of the window, I call to mind the green tinge of Niagara or the blue of the Rhone, that is no inference. In inference one belief not only follows after another, but follows from it.
54. What does that mean? The proper method of finding the answer to this question is to compare pairs of beliefs which differ as little as possible except in that in one pair one belief follows from the other and in the other pair only follows after it; and then note what practical difference, or difference that might become practical, there is between those two pairs. . . .
55. I think the upshot of reflection will be this. If a belief is produced for the first time directly after a judgment or colligation of judgments and is suggested by them, then that belief must be considered as the result of and as following from those judgments. The idea which is the matter of the belief is suggested by the idea in those judgments according to some habit of association, and the peculiar character of believing the idea really is so, is derived from the same element in the judgments. Thus, inference has at least two elements: the one is the suggestion of one idea by another according to the law of association, while the other is the carrying forward of the asserting element of judgment, the holding for true, from the first judgment to the second. That these two things suffice [to] constitute inference I do not say. . . . †1
56. †2 Let us now inquire in what the assertory element of a judgment consists. What is there in an assertion which makes it more than a mere complication of ideas? What is the difference between throwing out the word speaking monkey, and averring that monkeys speak, and inquiring whether monkeys speak or not? This is a difficult question.
In the first place, it is to be remarked that the first expression signifies nothing. The grammarians call it an "incomplete speech." But, in fact, it is no speech at all. As well call the termination ability — or ationally an incomplete speech. It is also to be remarked that the number of languages in which such an expression is possible is very small. In most languages that have nouns and adjectives, the participial adjective follows the noun and when left without other words the combination would mean the monkey is speaking.
In such languages you can't say "speaking monkey," and surely it is no defect in them; for after it is said, it is pure nonsense. . . . There are more than a dozen different families of languages, differing radically in their manner of thinking; and I believe it is fair to say that among these the Indo-European is only one in which words which are distinctively common nouns are numerous. And since a noun or combination of nouns by itself says nothing, I do not know why the logician should be required to take account of it at all. Even in Indo-European speech the linguists tell us that the roots are all verbs. It seems that, speaking broadly, ordinary words in the bulk of languages are assertory. They assert as soon as they are in any way attached to any object. If you write GLASS upon a case, you will be understood to mean that the case contains glass. It seems certainly the truest statement for most languages to say that a symbol is a conventional sign which being attached to an object signifies that that object has certain characters. But a symbol, in itself, is a mere dream; it does not show what it is talking about. It needs to be connected with its object. For that purpose, an index is indispensable. No other kind of sign will answer the purpose. That a word cannot in strictness of speech be an index is evident from this, that a word is general — it occurs often, and every time it occurs, it is the same word, and if it has any meaning as a word, it has the same meaning every time it occurs; while an index is essentially an affair of here and now, its office being to bring the thought to a particular experience, or series of experiences connected by dynamical relations. A meaning is the associations of a word with images, its dream exciting power. An index has nothing to do with meanings; it has to bring the hearer to share the experience of the speaker by showing what he is talking about. The words this and that are indicative words. They apply to different things every time they occur.
It is the connection of an indicative word to a symbolic word which makes an assertion.
57. †1 The distinction between an assertion and an interrogatory sentence is of secondary importance. An assertion has its modality, or measure of assurance, and a question generally involves as part of it an assertion of emphatically low modality. In addition to that, it is intended to stimulate the hearer to make an answer. This is a rhetorical function which needs no special grammatical form. If in wandering about the country, I wish to inquire the way to town, I can perfectly do so by assertion, without drawing upon the interrogative form of syntax. Thus I may say, "This road leads, perhaps, to the city. I wish to know what you think about it." The most suitable way of expressing a question would, from a logical point of view, seem to be by an interjection: "This road leads, perhaps, to the city, eh?"
58. An index, then, is quite essential to a speech and a symbol equally so. We find in grammatical forms of syntax, a part of the sentence particularly appropriate to the index, another particularly appropriate to the symbol. The former is the grammatical subject, the latter the grammatical predicate. In the logical analysis of the sentence, we disregard the forms and consider the sense. Isolating the indices as well as we can, of which there will generally be a number, we term them the logical subjects, though more or less of the symbolic element will adhere to them unless we make our analysis more recondite than it is commonly worth while to do; while the purely symbolic parts, or the parts whose indicative character needs no particular notice, will be called the logical predicate. As the analysis may be more or less perfect — and perfect analyses are very complicated — different lines of demarcation will be possible between the two logical members. †1 In the sentence "John marries the mother of Thomas," John and Thomas are the logical subjects, marries-the-mother-of- is the logical predicate. . . .
59. In making general assertions it is not possible directly to indicate anything but the real world, or whatever world discourse may refer to. But it is necessary to give a general direction as to the manner in which an object intended may be found. Especially it is necessary to be able to say that any object whatever will answer the purpose, in which case the subject is said to be universal, and to be able to say that a suitable object occurs, in which case the subject is said to be particular.
60. If there are several subjects, some universal and some particular, it makes a difference in what order the selections of a universal and of a particular subject are made. For example, the four following statements are different:
1. Take any two things, A and C; then a thing, B, can be so chosen that if A and C are men, B is a man praised by A to C.
2. Take anything, A; then a thing, B, can be so chosen, that whatever third thing, C, be taken, if A and C are men, B is a man praised by A to C.
3. Take anything, C; then a thing, B, can be so chosen, that whatever third thing, A, be taken, if A and C are men, B is a man praised by A to C.
4. A thing, B, can be so chosen that whatever things A and C may be, if A and C are men, B is a man praised by A to C.
We should usually express these as follows:
1. Every man praises some man or other to each man.
2. Every man praises some man to all men.
3. To every man some man is praised by all men.
4. There is a man whom all men praise to all men. †1
61. . . . When we busy ourselves to find the answer to a question, we are going upon the hope that there is an answer, which can be called the answer, that is, the final answer. It may be there is none. If any profound and learned member of the German Shakespearian Society were to start the inquiry how long since Polonius had had his hair cut at the time of his death, perhaps the only reply that could be made would be that Polonius was nothing but a creature of Shakespeare's brain, and that Shakespeare never thought of the point raised. Now it is certainly conceivable that this world which we call the real world is not perfectly real but that there are things similarly indeterminate. We cannot be sure that it is not so. In reference, however, to the particular question which at any time we have in hand, we hope there is an answer, or something pretty close to an answer, which sufficient inquiry will compel us to accept.
62. Suppose our opinion with reference to a given question to be quite settled, so that inquiry, no matter how far pushed, has no surprises for us on this point. Then we may be said to have attained perfect knowledge about that question. True, it is conceivable that somebody else should attain to a like "perfect knowledge," which should conflict with ours. He might know something to be white, which we should know was black. This is conceivable; but it is not possible, considering the social nature of man, if we two are ever to compare notes; and if we never do compare notes, and no third party talks with both and makes the comparison, it is difficult to see what meaning there is in saying we disagree. When we come to study the principle of continuity †1 we shall gain a more ontological conception of knowledge and of reality; but even that will not shake the definition we now give.
63. Perhaps we may already have attained to perfect knowledge about a number of questions; but we cannot have an unshakable opinion that we have attained such perfect knowledge about any given question. That would be not only perfectly to know, but perfectly to know that we do perfectly know, which is what is called sure knowledge. No doubt, many people opine that they surely know certain things; but after they have read this book, I hope many of them will be led to see that that opinion is not unshakable. At any rate, as they are, after all, in some measure reasonable beings, no matter how pig-headed they might be (I am only saying that pigheaded people exist, not that they are very frequently met with among my opponents), after a time, if they live long enough, reason must get the better of obstinate adherence to their opinion, and they must come to see that sure knowledge is impossible.
64. Nevertheless, in every state of intellectual development and of information, there are things that seem to us sure, because no little ingenuity and reflection is needed to see how anything can be false which all our previous experience seems to support; so that even though we tell ourselves we are not sure, we cannot clearly see how we fail of being so. Practically, therefore, life is not long enough for a given individual to rake up doubts about everything; and so, however strenuously he may hold to the doctrine of catalepsy, he will practically treat one proposition and another as certain. This is a state of practically perfect belief.
65. We have now to define the five words necessary, unnecessary, possible, impossible, and contingent. But first let me say that I use the word information to mean a state of knowledge, which may range from total ignorance of everything except the meanings of words up to omniscience; and by informational I mean relative to such a state of knowledge. Thus, by "informationally possible," I mean possible so far as we, or the persons considered, know. Then, the informationally possible is that which in a given information is not perfectly known not to be true. The informationally necessary is that which is perfectly known to be true. The informationally contingent, which in the given information remains uncertain, that is, at once possible and unnecessary.
66. The information considered may be our actual information. In that case, we may speak of what is possible, necessary, or contingent, for the present. Or it may be some hypothetical state of knowledge. Imagining ourselves to be thoroughly acquainted with all the laws of nature and their consequences, but to be ignorant of all particular facts, what we should then not know not to be true is said to be physically possible; and the phrase physically necessary has an analogous meaning. If we imagine ourselves to know what the resources of men are, but not what their dispositions and desires are, what we do not know will not be done is said to be practically possible; and the phrase practically necessary bears an analogous signification. Thus, the possible varies its meaning continually. We speak of things mathematically and metaphysically possible, meaning states of things which the most perfect mathematician or metaphysician does not qua mathematician or metaphysician know not to be true.
67. There are two meanings of the words possible and necessary which are of special interest to the logician more than to other men. These refer to the states of information in which we are supposed to know nothing, except the meanings of words, and their consequences, and in which we are supposed to know everything. These I term essential and substantial possibility, respectively: and of course necessity has similar varieties. That is essentially or logically possible which a person who knows no facts, though perfectly au fait at reasoning and well-acquainted with the words involved, is unable to pronounce untrue. The essentially or logically necessary is that which such a person knows is true. For instance, he would not know whether there was or was not such an animal as a basilisk, or whether there are any such things as serpents, cocks, and eggs; but he would know that every basilisk there may be has been hatched by a serpent from a cock's egg. That is essentially necessary; because that is what the word basilisk means. On the other hand, the substantially possible refers to the information of a person who knows everything now existing, whether particular fact or law, together with all their consequences. This does not go so far as the omniscience of God; for those who admit Free-Will suppose that God has a direct intuitive knowledge of future events even though there be nothing in the present to determine them. That is to say, they suppose that a man is perfectly free to do or not do a given act; and yet that God already knows whether he will or will not do it. This seems to most persons flatly self-contradictory; and so it is, if we conceive God's knowledge to be among the things which exist at the present time. But it is a degraded conception to conceive God as subject to Time, which is rather one of His creatures. Literal fore-knowledge is certainly contradictory to literal freedom. But if we say that though God knows (using the word knows in a trans-temporal sense) he never did know, does not know, and never will know, then his knowledge in no wise interferes with freedom. The terms, substantial necessity and substantial possibility, however, refer to supposed information of the present in the present, including among the objects known all existing laws as well as special facts. In this sense, everything in the present which is possible is also necessary, and there is no present contingent. But we may suppose there are "future contingents." Many men are so cocksure that necessity governs everything that they deny that there is anything substantially contingent. But it will be shown in the course of this treatise that they are unwarrantably confident, that wanting omniscience we ought to presume there may be things substantially contingent, and further that there is overwhelming evidence that such things are. . . . †1
68. To conclude from the above definitions that there is nothing analogous to possibility and necessity in the real world, but that these modes appertain only to the particular limited information which we possess, would be even less defensible than to draw precisely the opposite conclusion from the same premisses. It is a style of reasoning most absurd. Unfortunately, it is so common, that the moment a writer sets down these definitions nine out of ten critics will set him down as a nominalist. The question of realism and nominalism, which means the question how far real facts are analogous to logical relations, and why, is a very serious one, which has to be carefully and deliberately studied, and not decided offhand, and not decided on the ground that one or another answer to it is "inconceivable." Nothing is "inconceivable" to a man who sets seriously about the conceiving of it. †1 There are those who believe in their own existence, because its opposite is inconceivable; yet the most balsamic of all the sweets of sweet philosophy is the lesson that personal existence is an illusion and a practical joke. Those that have loved themselves and not their neighbors will find themselves April fools when the great April opens the truth that neither selves nor neighborselves were anything more than vicinities; while the love they would not entertain was the essence of every scent. †2
69. A leading principle of inference which can lead from a true premiss to a false conclusion is insofar bad; but insofar as it can only lead either from a false premiss or to a true conclusion, it is satisfactory; and whether it leads from false to false, from true to true, or from false to true, it is equally satisfactory. The first part of this theorem, that an inference from true to false is bad, [follows] from the essential characteristic of truth, which is its finality. For truth being our end and being able to endure, it can only be a false maxim which represents it as destroying itself. Indeed, I do not see how anybody can fail to admit that (other things being equal) it is a fault in a mode of inference that it can lead from truth to falsity. But it is by no means as evident that an inference from false to false is as satisfactory as an inference from true to true; still less, that such a one is as satisfactory as an inference from false to true. The Hegelian logicians seem to rate only that reasoning A1 which setting out from falsity leads to truth. But men of laboratories consider those truths as small that only an inward necessity compels. It is the great compulsion of the Experience of nature which they worship. On the other hand, the men of seminaries sneer at nature; the great truths for them are the inward ones. Their god is enthroned in the depths of the soul. How shall we decide the question? Let us rationally inquire into it, subordinating personal prepossessions in view of the fact that whichever way these prepossessions incline, we can but admit that wiser men than we, more sober-minded men than we, and humbler searchers after truth, do today embrace the opinion the opposite of our own. How, then, shall we decide the question? Yes, how to decide questions is precisely the question to be decided. One thing the laboratory-philosophers ought to grant: that when a question can be satisfactorily decided in a few moments by calculation, it would be foolish to spend much time in trying to answer it by experiment. Nevertheless, this is just what they are doing every day. The wisest-looking man I ever saw, with a vast domelike cranium and a weightiness of discourse that left Solon in the distance, once spent a month or more in dropping a stick on the floor and seeing how often it would fall on a crack; because that ratio of frequency afforded a means of ascertaining the value of {p}, though not near so close as it could be calculated in five minutes; and what he did it for was never made clear. Perhaps it was only for relaxation; though some people might have found reading Goldsmith or Voltaire fully as lively an occupation. If it were not for the example of this distinguished LL.D., I should have ventured to say that nothing is more foolish than carrying a question into a laboratory until reflection has done all that it can do towards clearing it up — at least, all that it can do for the time being. Of course, for a seminary-philosopher, to send a question to the laboratory is to have done with it, to which he naturally has a reluctance; while the laboratory-philosopher is impatient to get a whack at it.
70. Suppose that, at any rate, we try applying this maxim of methodology to the question now in hand. Then the first thing that has to be remarked is that every inference proceeds according to a general rule — and that, a comprehended rule — so that in the very act of drawing it the reasoner thinks of there being other similar inferences to be drawn. For unless the premiss determines the conclusion according to a rule, there is no intelligible meaning in saying that it determines it at all; unless, indeed, we are prepared to say that the conclusion feels compelled but knows not how; and if it knows not how, how can it know it was the premiss which compelled it? But a conclusion is not only determined by the premiss, but rationally determined, and that implies that in drawing said conclusion we feel we are following a rule and a comprehensible rule. . . .
71. Descartes marks the period when Philosophy put off childish things and began to be a conceited young man. By the time the young man has grown to be an old man, he will have learned that traditions are precious treasures, while iconoclastic inventions are always cheap and often nasty. He will learn that when one's opinion is beseiged and one is pushed by questions from one reason to another behind it, there is nothing illogical in saying at last, "Well, this is what we have always thought; this has been assumed for thousands of years without inconvenience." The childishness only comes in when tradition, instead of being respected, is treated as something infallible before which the reason of man is to prostrate itself, and which it is shocking to deny. In 1637, Descartes (aged 41) published his first work on philosophy, the Discours de la méthode pour bien conduise sa raison et chercher la verité dans les sciences. In the fourth part of this dissertation, after insisting upon the doubtfulness of everything, even the simplest propositions of mathematics, in a strain quite familiar to readers of the present work, he goes on to say how at one time "je me résolus de feindre que toutes les choses qui m'étoient jamais entrées en esprit n'étoient non plus vraies que les illusions de mes songes." Thereupon follows the grand passage: "Mais aussitôt après je pris garde que, pendant que je voulais ainsi penser que tout étoit faux, il falloit nécessairement que moi qui le pensois susse quelque chose; et, remarquant que cette vérité: je pense, donc je suis, étoit si ferme et si assurée que toutes les plus extravagantes suppositions des sceptiques n'étoient pas capable de l'ébranler, je jugeai que je pouvois la recevoir sans scrupule pour le premier principe de la philosophie que je cherchois."
Descartes thought this "très-clair"; but it is a fundamental mistake to suppose that an idea which stands isolated can be otherwise than perfectly blind. He professes to doubt the testimony of his memory; and in that case all that is left is a vague indescribable idea. There is no warrant for putting it into the first person singular. "I think" begs the question. "There is an idea: therefore, I am," it may be contended represents a compulsion of thought; but it is not a rational compulsion. There is nothing clear in it. Here is a man who utterly disbelieves and almost denies the dicta of memory. He notices an idea, and then he thinks he exists. The ego of which he thinks is nothing but a holder together of ideas. But if memory lies there may be only one idea. If that one idea suggests a holder-together of ideas, how it can do so is a mystery. To make the reflection that many of the things which appear certain to us are probably false, and that there is not one which may not be among the errors, is very sensible. But to make believe one does not believe anything is an idle and self-deceptive pretence. Of the things which seem to us clearly true, probably the majority are approximations to the truth. We never can attain absolute certainty; but such clearness and evidence as a truth can acquire will consist in its appearing to form an integral unbroken part of the great body of truth. If we could reduce ourselves to a single belief, or to only two or three, those few would not appear reasonable or clear.
72. Now, then, how is truth to be inferred from falsehood? First, it may happen accidentally, from the falsehood that Alexander the Great was the great-grandson of Benjamin Franklin it may be inferred there lived a great-grandson of Benjamin Franklin named Alexander, which happens to be true. It cannot be considered as a merit of a rule that its results accidentally have any character; for an accidental result ex vi termini is not determined by the rule. Secondly, truth may follow from falsehood because no lie is altogether false. Every precept of inference which does not lead from truth to falsity, must sometimes lead from falsity to truth. For let A be a true premiss and B a conclusion from it according to such a precept. Then B must be true. But if we add to A something false, B will follow from it just the same. A mode of inference may accordingly infer a larger proportion of true conclusions from false premisses than another simply by inferring less. But concluding falsehood from falsehood is by no means useless, provided it follows a precept which cannot conclude falsehood from truth. For it hastens the detection and rejection of the falsity. Consequently of two modes of inference neither ever leading from truth to falsity, one of which infers something false from a false premiss from which the other infers something true, the former is rather to be preferred because it infers more. Suppose for instance it is false that the sides of a triangle measure 4 inches, 5 inches, and 6 inches, then the rule of inference which deduces for the area 15/4 √7 square inches is certainly superior to a rule of inference which only concludes that the area is finite. Thirdly, truth may follow from falsehood because that falsehood is impossible and refutes itself. But in this way, only what is logically necessary can be inferred, that is only what a person ought to know independently of any particular premisses. As this is a mode of inference which infers less than any other, its value is the least that any mode can have which never leads from truth to falsity. Many persons will be inclined to dispute this, and will point to the utility of the reductio ad absurdum in geometry. But the reductio ad absurdum is not a method of inferring truth from falsity; it is only a form of statement of an inference from truth to truth. . . . †1
Now it may be that everything is so bound up with everything else that to understand perfectly any single fact, as it really is, would involve a knowledge of all facts. But this is not admitting that from any proposition, understood as it is understood, and not as the reality it represents ought to be understood, much can be inferred; far less that valuable truth can be deduced from falsehood.
It thus appears that the inference of truth from falsity is never so valuable as when it is accidental, in which case its value is precisely the same as that of an inference from false to false.
73. The inference from true to true has precisely the same value as that from false to false. For to infer B from A involves inferring the falsity of A from the falsity of B. The two inferences are inseparable; when either is made the other is made. Now if either of these is an inference from truth to truth, the other is an inference from falsity to falsity; and conversely, if either is an inference from false to false, the other is an inference from true to true. Accordingly it is impossible to set different values upon the two modes of inference.
74. Leading principles are of two classes: those whose pretension it is to lead always to the truth unless from the false, and never astray; and those which only profess to lead toward the truth in the long run. This distinction separates two great branches of reasoning, the one bringing to light the dark things of the hidden recesses of the soul, the other those hidden in nature. We may, for the present, call them Imaginative and Experiential reasoning; or reasoning by diagrams and reasoning by experiments. †1
75. . . . The necessity for a sign directly monstrative of the connection of premiss and conclusion is susceptible of proof. That proof is as follows. When we contemplate the premiss, we mentally perceive that that being true the conclusion is true. I say we perceive it, because clear knowledge follows contemplation without any intermediate process. Since the conclusion becomes certain, there is some state at which it becomes directly certain. Now this no symbol can show; for a symbol is an indirect sign depending on the association of ideas. Hence, a sign directly exhibiting the mode of relation is required. This promised proof presents this difficulty: namely, it requires the reader actually to think in order to see the force of it. That is to say, he must represent the state of things considered in a direct imaginative way.
76. A large part of logic will consist in the study of the different monstrative signs, or icons, serviceable in reasoning.
Suppose we reason
Enoch was a man,
Then, Enoch must have died.
Let this reasoning be called in question, and the reasoner searches his mind to discover the leading principle which actuated it. He finds this in the truth (as he assumes it to be) that
Every man dies.
He now repeats his reasoning, joining this proposition to the premiss previously assumed, to make the compound premiss,
Enoch was a man, and every man dies.
This may be otherwise stated thus:
If we are talking of Enoch, what we are talking of is a man; and if we are talking of a man, what we are talking of dies.
The conclusion is
If we are talking of Enoch, what we are talking of dies.
Or we may state it thus:
From being Enoch follows being a man, and from being a man follows being subject to death;
Hence, from being Enoch follows being subject to death.
If this reasoning is called in question, the reasoner searches his mind for the leading principle and may state it thus:
If one truth, A, makes another truth, B, certain, and if this truth, B, makes a third truth, C, certain; then, the truth, A, makes the truth, C, certain.
This is the logical principle called the Nota notæ, because one statement of it is, nota notæ est nota rei ipsius. †1
Now shall the reader add this as a premiss to the compound premiss already adopted? He gains nothing by doing so. For he cannot reason at all without a monstrative sign of illation; and this sign is not really monstrative unless it makes clear the proposition here proposed to be abstractly stated. Nor could any use of that statement be made without using the truth which it expresses.
That if the fact A is certain evidence of the fact B and the fact B is certain evidence of the fact C, then the fact A is certain evidence of the fact C, appears to us perfectly clear. That appearance of evidence may be an argument that the proposition is probably about true; for our instincts are generally pretty well adapted to their ends. But its appearing clear will not prevent our reflecting that things that seem evident are often found to be mistakes, so that it may be the proposition is not true.
77. Now although the reader does not really doubt that the proposition is true, it may be instructive to feign such a doubt, and see what the nature of the source of knowledge is.
A common form of the maxim is this: The word mortal is applicable to everything to which the word man is applicable, and the word man is applicable to everything to which the word Enoch is applicable. Hence, the word mortal is applicable to everything to which the word Enoch is applicable. This mode of representing the matter is embodied in a maxim called the Dictum de omni: †1 if A is in any relation to all to which B is in the same relation, and if B is in this relation to all to which C is in this relation, then A is in this relation to all to which C is in this relation; that is, if the things to which A is applicable are wholly included among the things to which B is applicable, and the things to which B is applicable are wholly included among the things to which C is applicable, then the things to which A is applicable are wholly included among the things to which C is applicable.
Here we have a mental diagram representing receptacles or spaces successively included in one another; and the question of the truth of the maxim may be divided into two parts:
First: Is the maxim certainly true of the mental diagram; and if so how do we know it?
Second: Does the mental diagram represent the relations of truths of nature to one another, in fact?
As to the first question, there would seem to be no reason to doubt that we know it is true of our mental diagram, just as we know of our idea of numbers that 2 and 3 make 5. And no line can be drawn between this case and knowing that √2=1.414213562373095 except that the latter is more complicated. It would thus appear that our certainty about the mental diagram is merely due to our having gone over it many times and being confident we could not be all wrong about a matter so simple. Still, as it is easy to make a mistake in calculating the √2, and that mistake may be repeated, it is barely possible that any conclusion reached in the same way is wrong. Besides, how do I know I am not crazy and am not uttering the greatest absurdity when I enunciate the Nota notæ? Of course, it is not rational for a man to assume that he is utterly irrational. A man cannot be speaking the truth in saying that everything he says is false. For this very thing is one of the things he says; and if this be false then in what it says of itself it is true, and therefore false. †1 But this remark does not clear up the matter; and we shall leave the problem for the present, to return to it later. †2
As to the second question, it is important to remark that the Nota notæ does not declare that there is any infallible mark of anything, or any rule without exceptions. If, as we have seen, the Nota notæ itself is not absolutely certain, nothing else ought to be so regarded. We cannot go so far as to declare that absolutely no rule is without exceptions; for this declaration is itself a rule. Nor can we say that no rule but this is without exceptions. For this rule either has exceptions or it has not. If it has exceptions and every other rule has exceptions, it has no exceptions. But if it has no exceptions, then in accordance with its declaration it has exceptions. We are thus obliged to admit that there are rules without exceptions, or at least that the denial of it has no sense. †P1 But we ought not to suppose that we can identify any general proposition as being certainly or even probably without exceptions. The case is like the following. We say 1/2 of 1/3 is 1/6. Now we do not really think we can divide anything into precisely equal parts; but we think that, barring the possibility that we have made a mistake in doing the sum, which is excessively improbable, the nearer we can come to 1/2 of 1/3 of anything, that is, to the ideal state of things in our imagination, the nearer we shall come to 1/6 . . .
78. In like manner, it may be nothing in the world precisely conforms to rigidity of our idea of something steady enough to be represented by a sign. The reader has had several examples of insolubilia, †1 as they are called by logicians, that is, cases in which every attempt to reason lands us in absurdity. Here are two more examples.
In order to prove black is white, you have only to say, "Either what I am saying is false or black is white." Is that proposition false? It cannot be so; for it only says that one or other of two things is true; and if either is true the proposition is true. It cannot, therefore, be false; for that is one of the alternatives that it leaves open. The proposition is true, then. Consequently, one of the alternatives is true. But not the first; therefore the second. Hence, black is white.
A man invented an ink containing Vanadium the like of which had never been made before. He was just about to try it for the first time, when a friend asked, "Has anything ever been written in Vanadium ink before?" "No." "Will you please write what I tell you for the first handsel of it?" "Yes." "Very well, here is a folded paper marked 'Exhibit A.' Write: What is written in exhibit A is true." He did so. "Now," said the friend, "do you know you have lied to me?" "Oh, but I only wrote that to please you. I did not mean to say it was true." "Very well; suppose it false. Then, what exhibit A says is false. Now read Exhibit A. It reads: 'Something written in Vanadium ink is false.' If that is false, what you have written must be true." "Good! So much the better!" "Not so fast, if you please. What you have written is, of course, true; and consequently exhibit A is true; and consequently something written in Vanadium ink is false. Now it is not what you have just written, for that is true; and therefore you must have lied when you told me nothing had ever been written with that ink before."
It may be that all the propositions in the world would, if subjected to a dialectical examination, prove thus elusive. But that does not affect the truth of the Nota notæ, which only says that so far as things conform to our idea of successive inclusion, so far (unless we have blundered almost inconceivably) the Nota notæ holds. . . .
79. The logician does not assert anything, as the geometrician does; but there are certain assumed truths which he hopes for, relies upon, banks upon, in a way quite foreign to the arithmetician. Logic teaches us to expect some residue of dreaminess in the world, and even self-contradictions; but we do not expect to be brought face to face with any such phenomenon, and at any rate are forced to run the risk of it. The assumptions of logic differ from those of geometry, not merely in not being assertorically held, but also in being much less definite.
Paper 3: Second Intentional LogicP †1
80. Second intentional, or, as I also call it, Objective Logic, is much the larger part of formal logic. It is also the more beautiful and the interesting subject; and in serious significance it is superior in a far higher ratio. But it is highly abstract, remote from the bread and butter of all parties, and to yield to the temptation of going into it would be to forget
| That not to know at large of things remote | |
| From use, obscure and suttle, but to know | |
| That which before us lies in daily life, | |
| Is the prime Wisdom, what is more is fume, | |
| Or emptiness, or fond impertinence, | |
| And renders us in things that most concerne | |
| Unpractis'd, unprepar'd, and still to seek. |
81. Second intentional logic treats at length of the properties of logical conceptions. First, come such simple relations as 0, ∞, 1, T. †2 There is also an extensive doctrine concerning q, the relation of inherence. Kant, in his celebrated Appendix to the Transcendental Dialectic, †3 has set forth three sporadic propositions of this sort, whose significance can hardly be seen away from their crowd. Besides, it is more satisfactory to see these things set forth in a purely logical way and deduced mathematically, than to have them treated at their first presentation as regulative principles. As a part of this general doctrine of inherence, there is a special doctrine of the properties of relations. Of course, all logical treatises consider these things; but they do not consider them in a formal way, nor at all in the manner in which they are turned out by the machinery of this calculus. One of the questions which pertain to this branch of logic is that of the classification of relations. There are also some special relations of logical origin which have to be considered, among which is that of correspondence, which has been studied by mathematicians without much logical analysis.
82. A number of interesting features of the logical calculus itself emerge in the application of it to the second intentions. One of these, for example, is that the subjacent letters I call indices do not essentially differ from any other letters. Thus we may define identity as follows:
That is, to say that anything whatever, K, is identity is to say that if any two things i and j are in the relation, K, the i to the j, then any proposition whatever, x, is true of i, or else that proposition is false of j. The point calling for notice is that x is put into the logisterium, although it is one of the principal letters of the Boolian. †1
83. Another thing is that the forms of logisteria, themselves, become subjects of study, and certain general propositions with regard to them are expressed as if they were shops or trees; and yet these very propositions can be made use of in the calculus.
Among the forms of logisteria which require attentive study and which are found to possess interesting properties are particularly those which are infinite series, though the very purpose of the lectical symbols is to embrace infinite series. But we find that we have to resort to logisteria of logisteria, and to their logisteria again, and so on indefinitely, and that the distinctive characters of different such infinite series of logisteria have to be discriminated.
84. Another point of logical interest is that when our discourse relates to a universe of possibility which virtually embraces all logical possibility, everything is true from which no false consequence can possibly follow; and the only way of investigating certain propositions is by proving that they cannot give rise to any contradiction; and this being proved, they are proved true.
For example, it is required to prove that
That is, that every object, a, whether individual or general, has a quality, K, which is a quality of no object, b, unless b is identical with a. Now this can only lead to an absurd result if K be eliminated. But without "logical involution," or the compounding of the premiss with itself, K can only be eliminated in two ways; first, by eliminating gKa and ḡKb independently, and second, by identifying b with a. In the first way, we can only get
which is true; and in the second way we can only get
Πa1aa
which is equally true. We next proceed, then, to square the proposition in question, and so get
ΠaΣKΠbΠc gKa·(ḡKb 1ab)·(~gKc
1ab)·(~gKc 1ac).
1ac).
Unless we identified K in the factors, there could be no aid in eliminating K. But this identification forces us to identify a which is to the left of it in the logisterium. But it is easy to show that from the square so written K cannot be eliminated in any new way, nor from any higher power. Therefore, the proposition can lead to no absurdity, and is true.
Suppose, however, we were to subject the following (which seems hardly distinguishable from it to a loose thinker) to the same test
Squaring this, we have
ΣKΠaΠbΠcΠd gKa·gKc·(~gKb 1ab)·(~gKd
1ab)·(~gKd 1cd).
1cd).
Now identifying d with a and c with b, we get
ΠaΠb1ab
which is as much as to say that everything is identical with everything. So that in a universe of more than one object this proposition is false.
Paper 4: The Logic of QuantityP †1
§1. Arithmetical Propositions
85. Kant, in the introduction to his Critic of the Pure Reason †2, started an extremely important question about the logic of mathematics. He begins by drawing a famous distinction, as follows:
"In judgments wherein the relation of a subject to a predicate is thought . . . this relation may be of two kinds. Either the predicate, B, belongs to the subject, A, as something covertly contained in A as a concept; or B is external to A, though connected with it. In the former case, I term the judgment analytical; in the latter synthetical. Analytical judgments, then, are those in which the connection of the predicate with the subject is thought to consist in identity, while those in which this connection is thought without identity, are to be called synthetical judgments. The former may also be called explicative, the latter ampliative judgments, since those by their predicates add nothing to the concept of the subject, which is only divided by analysis into partial concepts that were already thought in it though confusedly; while these add to the concept of the subject a predicate not thought in it at all, and not to be extracted from it by any analysis. For instance, if I say all bodies are extended, this is an analytical judgment. For I need not go out of the conception I attach to the word body, to find extension joined to it; it is enough to analyze my meaning, i.e., merely to become aware of the various things I always think in it, to find that predicate among them. On the other hand, if I say, all bodies are heavy, that predicate is quite another matter from anything I think in the mere concept of a body in general."
Like much of Kant's thought this is acute and rests on a solid basis, too; and yet is seriously inaccurate. The first criticism to be made upon it is, that it confuses together a question of psychology with a question of logic, and that most disadvantageously; for on the question of psychology, there is hardly any room for anybody to maintain Kant right. Kant reasons as if, in our thoughts, we made logical definitions of things we reason about! How grotesquely this misrepresents the facts, is shown by this, that there are thousands of people who, believing in the atoms of Boscovich, do not hold bodies to occupy any space. Yet it never occurred to them, or to anybody, that they did not believe in corporeal substance. It is only the scientific man, and the logician who makes definitions, or cares for them.
86. At the same time, the unscientific, as well as the scientific, frequently have occasion to ask whether something is consistent with their own or somebody's meaning; and that sort of question they themselves widely separate from a question of how experience, past or possible, is qualified. The Aristotelian [logicians] — and, in fact, all men who ever have thought — have made that distinction. It is embodied in the conjugations of some barbarous languages. What was peculiar to Kant — it came from his thin study of syllogistic figure-was his way of putting the distinction, when he says we necessarily think the explicatory proposition although confusedly, whenever we think its subject. This is monstrous! The question whether a given thing is consistent with a hypothesis, is the question of whether they are logically compossible or not. I can easily throw all the axioms of number, which are neither numerous nor complicated, into the antecedent of a proposition — or into its subject, if that be insisted upon — so that the question of whether every number is the sum of three cubes, is simply a question of whether that is involved in the conception of the subject and nothing more. But to say that because the answer is involved in the conception of the subject, it is confusedly thought in it, is a great error. To be involved, is a phrase to which nobody before Kant ever gave such a psychological meaning. Everything is involved which can be evolved. But how does this evolution of necessary consequences take place? We can answer for ourselves after having worked a while in the logic of relatives. It is not by a simple mental stare, or strain of mental vision. It is by manipulating on paper, or in the fancy, formulæ or other diagrams — experimenting on them, experiencing the thing. Such experience alone evolves the reason hidden within us and as utterly hidden as gold ten feet below ground — and this experience only differs from what usually carries that name in that it brings out the reason hidden within and not the reason of Nature, as do the chemist's or physicist's experiments.
87. There is an immense distinction between the Inward and the Outward truth. I know them alike by experimentation only. But the distinction lies in this, that I can glut myself with experiments in the one case, while I find it most troublesome to obtain any that are satisfactory in the other. Over the Inward, I have considerable control, over the Outward very little. It is a question of degree only. Phenomena that inward force puts together appear similar; phenomena that outward force puts together appear contiguous. We can try experiments establishing similarity so easily, that it seems as if we could see through and through that; while contiguity strikes us as a marvel. The young chemist precipitates Prussian blue from two nearly colorless fluids a hundred times over without ceasing to marvel at it. Yet he finds no marvel in the fact that any one precipitate when compared in color with the other seems similar every time. It is quite as much a mystery, in truth, and you can no more get at the heart of it, than you can get at the heart of an onion.
But nothing could be more extravagant than to jump to the conclusion that because the distinction between the Inward and the Outward is merely one of how much, therefore it is unimportant; for the distinction between the unimportant and the important is itself purely one of little and much. Now, the difference between the Inward and the Outward worlds is certainly very, very great, with a remarkable absence of intermediate phenomena.
88. The first question, then, to ask concerning arithmetical and geometrical propositions is, whether they are logically necessary and merely relate to hypotheses, or whether they are logically contingent and relate to experiential fact.
Beginning with the propositions of arithmetic, we have seen already †1 that arithmetical propositions may be syllogistic conclusions from ordinary particular propositions. From
A B
and Ā B̿, †2
taken together, or
Some A is B,
Some not-A is B,
it follows that there are at least two B's. This inference is strictly logical, depending on the principle of contradiction, that is, on the non-identity of A and not-A. By the same principle, from
Some A is B,
Some not-A is B,
Any B is C,
Some not-B is C,
taken together it follows that there are at least three C's.
89. Hamilton admits †3 that the arithmetical proposition, "Some B is not some-B," is so urgently called for in logic, that a special propositional form must be made for it. So, if a distributive meaning be given to "every," Every A is every A, implies that there is but one A, at most. This is what this proposition must mean, if it is to be the precise contradiction of the other. If a proposition is infra-logical in form, its denial must be admitted to be so.
90. It clearly belongs to logic to evolve the consequences of its own forms. Hence, the whole of the theory of numbers belongs to logic; or rather, it would do so, were it not, as pure mathematics, prelogical, that is, even more abstract than logic. †4
91. These considerations are sufficient of themselves to refute Kant's doctrine that the propositions of arithmetic are "synthetical." As for the argument of J. S. Mill, †5 or what is usually attributed to him, for what this elusive writer really meant, if he precisely meant anything, about any difficult point, it is utterly impossible to determine — I mean the argument that because we can conceive of a world in which when two things were put together, a third should spring up, therefore arithmetical propositions are experiential, this argument proves too much. For, in the existing world, this often happens; and the fact that nobody dreams of its constituting any infringement of the truths of arithmetic shows that arithmetical propositions are not understood in any experiential sense.
But Mill is wrong in supposing that those who maintain that arithmetical propositions are logically necessary, are therein ipso facto saying that they are verbal in their nature. This is only the same old idea that Barbara in all its simplicity represents all there is to necessary reasoning, utterly overlooking the construction of a diagram, the mental experimentation, and the surprising novelty of many deductive discoveries.
If Mill wishes me to admit that experience is the only source of any kind of knowledge, I grant it at once, provided only that by experience he means personal history, life. But if he wants me to admit that inner experience is nothing, and that nothing of moment is found out by diagrams, he asks what cannot be granted.
92. The very word a priori involves the mistaken notion that the operations of demonstrative reasoning are nothing but applications of plain rules to plain cases. The really unobjectionable word is innate; for that may be innate which is very abstruse, and which we can only find out with extreme difficulty. All those Cartesians who advocated innate ideas took this ground; and only Locke failed to see that learning something from experience, and having been fully aware of it since birth, did not exhaust all possibilities.
Kant declares that the question of his great work is "How are synthetical judgments a priori possible?" By a priori he means universal; by synthetical, experiential (i.e., relating to experience, not necessarily derived wholly from experience). The true question for him should have been, "How are universal propositions relating to experience to be justified?" But let me not be understood to speak with anything less than profound and almost unparalleled admiration for that wonderful achievement, that indispensible stepping-stone of philosophy.
93. To return to number, there are various ways in which arithmetic may be conceived to connect itself with and spring out of logic. Besides the path of spurious propositions [as indicated in 88], there is another which I pursued on an early paper †1 in which I defined the arithmetical operations in terms of those of the reformed Boolian calculus. In a later paper, †2 I considered quantity from the point of view of the logic of relatives.
I shall in the present chapter endeavor, as much as I can, to avoid tedious questions of detail and seek to make clear some of the main points of the logic of mathematics.
§2. Transitive and Comparative Relations
94. I have certainly written to little purpose, and so has Dr. Schröder, if we have not succeeded in making readers perceive the pervasive working of balance and symmetry in every part of logic. Now, we have seen the ubiquitous logical agency of the form
ll̄̆. †3
We say that this is due to the formula ll̄̆ ⤙ T, †4 which is balanced by 1 †5 ⤙ l†l̄̆. †6 But, be it observed, that this is a kind of balance which throws all the active work upon the shoulders of the former principle, and allows the latter to moulder in innocuous desuetude. Yet really, the form
l†l̄̆
is all-important, inasmuch as it is the basis of all quantitative thought. For the relation expressed by it is a transitive relation. By a transitive relation, we mean a relation like that of the copula. If A be so related to B, and B be so related to C, then A is so related to C. In other words, if t is a transitive relation,
tt ⤙ t.
Now, this is the case with l†l̄̆. For that
(l†l̄̆)(l†l̄̆) ⤙ l†l̄̆
is obvious. Though the reader sees how, I will, in consideration of the importance of the matter, set down the steps:
| (l†l̄̆)(l†l̄̆) | |
| ⤙ | l†l̄̆(l†l̄̆) |
| ⤙ | l†l̄̆ l†l̄̆ |
| ⤙ | l†T†l̄̆ |
| ⤙ | l†l̄̆. |
This is not only a transitive relation, but it is one which includes identity under it. That is,
1 ⤙ l†l̄̆
But it is further demonstrable that every transitive relation which includes identity under it is of the form
l†l̄̆.
For let t be such a relation that
1 ⤙ t.
Multiplying by t̄̆, we get,
t̄̆ ⤙ 1t̄̆ ⤙ tt̄̆ ⤙ T.
Hence, †1
t†t̄̆ ⤙ t†T ⤙ t.
On the other hand,
| t ⤙ t1 | |
| ∴ | t ⤙ t(t†t̄̆) |
| ∴ | t ⤙ tt†t̄̆. |
But because t is transitive,
tt ⤙ t
∴ t ⤙ t†t̄̆.
Having just found
t†t̄̆ ⤙ t,
we can write
t = t†t̄̆,
so that t may be expressed in the form l†l̄̆, Q. E. D.
95. I am now going to allow myself to be led aside out of the main channel of thought upon this subject merely to show how little interest there is in transitive relationship apart from the logical form (l†l̄̆).
Let us use the zodiacal sign of Leo to signify a transitive relation, such that not everything is in that relation to itself. The inference holds,
x☊y, y☊z,
∴ x☊z.
Let L be an individual that is not in this relation to itself, which we may write,
L☊L.
Then, the (equivalent) inferences hold
| L☊x | x☊L | ||
| ∴ | x~☊L | ∴ | L~☊x. |
We may, therefore, divide all other individuals into three classes; first, K, J, etc. such that
K☊L
J☊L, etc.;
second, M, N, etc., such that
L☊M
L☊N, etc.;
and third, Γ, Δ, etc., such that
| Γ~☊L | L~☊Γ |
| Δ~☊L | L~☊Δ, etc. |
Taking any one of the first class, K, and any one of the second, M, we have
M~☊K.
Let G be a letter of the first class which is a non-Leo of itself; then
G~☊G,
and the first class may be subdivided into three with reference to G, just as all were divided relatively to L. So, if R be a letter of the second class which is non-Leo of itself, or
R~☊R.
We can then divide all possible individuals other than G, L, and R into ten classes, viz.:
First, Those which, as B, C, etc. are Leos of G; as
B☊G;
Second, Those which, as r, are neither Leos of nor Leo'd by G, but are Leos of L; as
Γ~☊G, G~☊Γ, Γ☊L;
Third, Those which, as H, K, etc., are Leo'd by G and are Leos of L; as
G☊K, K☊L;
Fourth, Those which, as Δ, are not Leo'd by G, nor are Leos of L, but are Leos of R; as
G~☊Δ, Δ~☊L, Δ☊R;
Fifth, Those which, as Θ, are Leo'd by G, are neither Leos of nor Leo'd by L, and are Leos of R; as
G☊Θ, L~☊Θ, Θ~☊L, Θ☊R;
Sixth, Those which, as P, Q, etc. are Leo'd by L and are Leos of R; as
L☊P, P☊R;
Seventh, Those which as Ξ are not Leo'd by G nor are Leos of R; as
G~☊Ξ, Ξ~☊R;
Eighth, Those which as Π are Leo'd by G, are not Leo'd by L, and are not Leos of R;
G☊Π, L~☊Π, Π~☊R;
Ninth, Those as Σ which are Leo'd by L but are neither Leos of nor Leo'd by R;
L☊Σ, R~☊Σ, Σ~☊R;
Tenth, Those as X, Y, etc. which are Leo'd by R; as
R☊X.
96. The above gives some idea what the further doctrine of transitive relations not including identity would be like. It is evidently more interesting to consider further the study of relatives of the form (l†l̄̆) and others allied to them.
The converse of l†l̄̆ is l̄†l̆, †1 which is, of course, also transitive. The negative is l̄l̆, †2 which is not transitive, but which has the property,
l̄l̆ ⤙ l̄l̆†l̄l̆.
For l̄l̆ = l̄1l̆ ⤙ l̄(l̆†l̄)l̆ ⤙ l̄l̆†l̄l̆.
This is a property allied to transitiveness.
If A is a lover of something not loved by B, which is, in its turn, a lover of something not loved by C, the conclusion is, that A is a lover of something different from something not loved by C. That is,
(ll̄̆)(ll̄̆) ⤙ lTl̄̆.
The natural current of thought next carries us to the hypothesis that the relation expressed by l be such that
ll̄̆ ⤙ l†l̄̆.
In this case, ll̄̆ is a transitive relation. For
ll̄̆ ll̄̆ ⤙ ll̄̆(l†l̄̆) ⤙ ll̄̆.
Such a relation may well be termed a comparative relation. If Samson can lift something Ajax cannot lift, then Samson can lift everything Ajax can lift. Such a relation underlies all measurement; and the propriety of the designation I propose will be allowed.
With this conception, quantitative science begins. Note well how it has been suggested to us.
A trial of strength must begin by young Ajax, the challenger, doing various things which he "stumps" the champion, Samson, to imitate. If Samson cannot perform all of Ajax's feats, that settles it. But if it seems that Samson can do all that Ajax can do then he will, in his turn, do something which he proposes that Ajax shall imitate. If Ajax cannot do all that Samson can do, that again settles it. But if it seems that each can repeat all the performances of the other, we conclude that they are equally strong. Thus equality is a complex relation. †3
In a universe of quantities of one dimension (where are only quantities, not quanta) things equal are identical; so that, not only,
ll̄̆ ⤙ T,
which is always true and
ll̄̆ ll̄̆ ⤙ T,
which is true for all comparative relations, but also
T ⤙ ll̄̆ l̄l̆. †1
l̄l̆. †1
That is, if A and B are not identical, either A can do something that B cannot, or B can do something that A cannot.
We have thus analyzed the conception of quantity; and we see that nothing but logical conceptions enter into its constitution. The idea of being able, especially in the broad sense in which one quantity is said to be able to do something another is unable to do, is only a modification of the idea of possibility, the precise explanation of which is given in second intentional logic.
97. Although I cannot, in this work, carry the student deeply into second intentional logic, yet it will be indispensible to look upon quantity somewhat in that way; for quantitative thought, like the traditional "chimæra bombinans in vacuo," feeds upon second intentions.
That l is a comparative relation in a universe of quantity, may be expressed by the formula,
0†(1 ll̄̆
ll̄̆ l̄l̆)†0 †1
l̄l̆)†0 †1
But the same thing may be expressed in another way, by throwing the relation l among the indices. Thus, let us use the three symbols, u, v, w.
wij means that i is an individual relation of which j is the general character,
uij means that i is an individual relation of which j is the first relate,
vij means that i is an individual relation of which j is the correlate.
Then, we shall have
lij = Σkukivkjwkl,
that is, there is an individual relation of which i is the relate, j the correlate, and l the general character.
That being premissed, the proposition that l is a comparative relation may be written,
ΠhΠkΣiΣjΣpΠqΠrΣs 1hk uph·vpi·wpl·(ūqk
uph·vpi·wpl·(ūqk v̄qi
v̄qi w̅ql)
w̅ql) (ūrh
(ūrh v̄rj
v̄rj w̅rl)·usk·vsj·wsl;
w̅rl)·usk·vsj·wsl;
that is, of any two different objects, h and k, one or other is l to something to which the other is not l.
More simply, if
rijk
means that i is a relation in which j stands to k; we may write,
ΠhΠkΣiΣj 1hk rlhir̄lki
rlhir̄lki rlkj~rlhj
rlkj~rlhj
to express that l is a comparative relation.
98. We are next naturally led to remark that it is a very important thing to say of a class of objects, say the A's, that there is some one relation such that, of any two A's not identical, one stands in that relation to the other, while the second does not stand in that relation to the first. This we write
ΣlΠmΠn Ām Ān
Ān 1mn
1mn rlmn~rlnm
rlmn~rlnm rlnm~rlmn
rlnm~rlmn
But this becomes particularly important, in case the relation l is a relation of comparison. If that be the case, we multiply in the above definition of such a relation.
99. The question arises, is it possible there should be a class which does not possess the property just defined? It is a difficult question, to which a good logician will be reluctant to give a negative answer. In order to answer it, we must have some way of constructing an icon of a class, in general. Now, a class may be said to comprise all of which something is true. Shall we say of the different individuals composing it that they are distinguished by having some of them qualities which the others do not possess? It seems far from evident that this is so; although, no doubt, after two instances have presented themselves, it is possible in the circumstances of the presentation to find distinguishing qualities. But supposing this difficulty surmounted, of two individuals of a class, each may have qualities the other wants. If, then, we seek to establish an order of precedence among the things, such as a relationship of comparison supposes, we must first establish some order of precedence among the qualities. We are thus brought back to the question with which we set out, whether among a collection of objects an order of precedence can always be establishable. It thus becomes clear that no contradiction can emerge from the hypothesis of a class among the members of which no thoroughgoing order of precedence can be established, and to which all quantitative conceptions are quite inapplicable. About such classes we can reason, but we cannot reason quantitatively.
§3. Enumerable Collections
100. But supposing we have to do with a class of things throughout which a relationship of comparison can be established, the next question that balance and symmetry suggest is, whether, as we have
l1̄̆ ll̄̆ ⤙ ll̄̆,
we have also
ll̄̆ ⤙ l1̄̆ ll̄̆.
It is clear enough, that cases can be imagined in which this shall not be true. Classes of a mixed character exist, too, where this holds in certain parts, but not in others. Such mixed cases are not, however, of much interest. The interesting cases are those in which
ll̄̆ ⤙ l1̄̆ ll̄̆
invariably holds, †1 and those in which whatever is ll̄̆ to anything is ll̄̆ to something to which it is not l1̄̆ ll̄̆. To speak in more familiar terms, whatever is greater than anything may or may not always be next greater than something, that is, may or may not be always greater than something else, greater than that thing.
101. But a further distinction immediately arises, according as, on the one hand, one or other of these propositions is true for every comparative relation, or on the other hand for some comparative relations the one proposition is true and for others the other.
This trichotomy constitutes the most important distinction between classes in respect to their multitude.
Let us first consider a class in which, no matter what comparative relation may be signified by ll̄̆,
ll̄̆∞ ⤙ [ll̄̆·(l̄†l̆†l̄†l̆)]∞. †1
That is, whatever is greater than anything is next greater than something, in every sense of being greater, that is, for every comparative relation, ll̄̆, for which
102. We have now pushed our way far enough into the theory of quantity and its complications of logic to meet with theorems. Such is the following: any class of which the conditions enunciated holds has a maximum and a minimum individual for each comparative relation, that is, one which is not ll̄̆ to any member of the class, and one which is not l̄l̆ to any member. I will first show that there is a maximum. For this purpose, assume a0 to be any member of the class of A's, and consider the relation
(ll̄̆ l̄l̆)a0ă0
l̄l̆)a0ă0 l1̄̆ a0ă0l̄l̆·ll̄̆
l1̄̆ a0ă0l̄l̆·ll̄̆ l̄l̆ a0ă0l̄l̆
l̄l̆ a0ă0l̄l̆ l̄l̆a0ă0ll̄̆·l̄l̆.
l̄l̆a0ă0ll̄̆·l̄l̆.
This is an aggregate of four relations, viz.:
First, That having for its relate any A, superior (ll̄̆) or inferior (l̄l̆) to a0, and for its correlate a0,
Second, That having for both relate and correlate A's superior to a0, the relate being superior to the correlate,
Third, That having for relate any A inferior to a0, and for correlate any A superior to a0,
Fourth, That having for both relate and correlate A's inferior to a0, the relate being inferior to the correlate.
This, I say, will be a quantitative relation. That is, it will be transitive, included under its own negative converse, and including negation under the aggregate of itself and its converse. That it is transitive, that is, that, if X is in this relation to Y, and Y to Z, then X is in this relation to Z, is plain; for, if Y is superior to a0, then Z must either be a0 (in which case, X, whatever A it may be, is in this relation to Z) or must be superior to a0 but inferior to Y. Then, if X is superior to a0, it is superior to Y, and consequently also to Z, and is in this relation to Z. But if X is inferior to a0, it is in this relation to Y, which is superior. X can in no case be a0. If Y is inferior to a0, Z is either a0 (when as before X will be in this relation to it) or superior to a0, or inferior to a0, but superior to Y. X will be inferior to Y, and thus will be in this relation to Z. This shows that the relation is transitive. That it is included under its negative converse, that is, inconsistent with its converse, is plain; for if U could be in this relation to V and in the converse relation, too, that is, V in this relation to U, then, since the relation is transitive, U would be in this relation to itself, which, it is easy to see, the definition excludes. That of any pair of different A's, one is in this relation to the other, is easily seen by running over the definition.
We will call this relation "second-superior." Now, I say, if the class of A's has no maximum for the relation ll̄̆, then that A which is next inferior to a0 is not next second-superior to any A. Will it be objected that I have not proved that there is an A next inferior to a0? It is easy to supply the defect. For by hypothesis whatever A is superior is next superior to some A for every comparative relation. Now, we have only to substitute l̆ for l and vice versa, and next inferior becomes next superior. Therefore, to say that for every comparative relation, whatever has a superior has a next superior, is the same as to say that for every comparative relation, whatever has an inferior has a next inferior. The A next inferior to a0 is second-superior only to a0, to A's superior to a0 and to A's inferior to a0 but superior to itself. Because it is next inferior, of the last there are none. That of which it is next superior is therefore superior to a0, and any other A superior to it is second-superior to it and second-inferior to the next inferior to a0. Thus, that to which the next inferior to a0 is next second-superior, is the superior of all other A's superior to a0; that is, it is the maximum. The proof that there will be a minimum is altogether similar.
Hence, any class of things in which whatever is anywise superior to another of the class is next superior to some one can be enumerated. For in enumeration, the objects of a class are singly told, and "told later than" evidently satisfies the three conditions of a quantitative relative. If there is a maximum, the telling comes to an end, the class is told out, it is enumerated. For that reason, it is convenient to term a class every member of which anywise superior to another is next superior to some, an enumerable collection.
103. †1 About an enumerable collection certain forms of reasoning hold which, though they had been used more or less since man began to be a reasoning animal, were first signalized in a logical work by De Morgan in 1847, †P1 and constitute one of his claims to be considered the greatest of all formal logicians. In his Formal Logic he gives eight forms which in the Appendix to his fourth Memoir on the Syllogism are increased to 64. The eight are as follows:
For every Z there is an X that is Y,
Some Z is not Y;
∴Some X is not Z.
For every Z there is an X not Y,
Some Z is Y;
∴Some X is not Z.
For every non-Z there is an X that is Y,
There is something besides Y's and Z's;
∴Some X is Z.
For every non-Z there is an X not Y,
Some Y is not Z;
∴Some X is Z.
For every Z there is a Y not X,
Some Z is not Y;
∴There is something besides X's and Z's.
For every Z there is something neither X nor Y,
Some Y is Z;
∴There is something besides X's and Z's.
For every non-Z there is a Y not X,
There is something besides Y's and Z's;
∴Some Z is not X.
For every non-Z there is something neither X nor Y,
Some Y is not Z;
∴Some Z is not X.
We might also have such a reasoning as this:
For every Z there is an X that is Y,
For every X not Z there is an X not Y;
∴Every Z is X.
This is not one of De Morgan's Forms. He gives, however such as these:
For every Z an X is Y,
Every Y is Z;
∴Every Z is X.
For every not Z is an X not Y,
For every X is a Y not Z;
∴Every Z is X.
De Morgan termed these "syllogisms of transposed quantity," because they transfer the lexis from one term to another. His point of view was this: Take Baroko,
Any M is P,
Some S is not P;
∴Some S is not M.
The converse,
Some M is not S,
does not follow; but if there are as many M's as there are S's, then this does follow. "For if M's, as many as there are S's, be among the P's, and some of the S's be not among the P's, though all the rest were, there would not be enough to match all the M's, or some M's are not S's."
The rank and file of old-fashioned logicians were not pleased with the syllogisms of transposed quantity. They belonged to that class of minds who decry originality, who dread novelty, who hate discoveries, and who will go to some trouble to inflict any personal injury on those who perpetrate them, provided they can inflict it without serious injury to themselves. They circulated an unfounded innuendo that De Morgan was a drunkard; their spitefulness was only bounded by their prudence. The idea of so lifeless a subject as formal logic — too abstract to be philosophical — exciting such passions is laughable. Yet such was the fact.
But they could not find anything better to say against those syllogisms of transposed quantity than that they were "extralogical." If it had only occurred to them that they were not sound reasoning, that is, not universally valid, they would have seized upon that defect with glee. Nor, singularly enough, does De Morgan himself seem to have remarked the circumstance; although it ought to have been evident from the line of thought which led him to those forms. By the logic of relatives, we at once find that the statement that such a syllogism is necessary implies that a certain collection is enumerable.
The following is the first form De Morgan adduced:
Some X is Y,
For every X there is something neither Y nor Z;
Hence, something is neither X nor Z.
Let us put for X "odd number," for Y "prime," for Z "either an even number or not a number," so that its negative is "a number not even." Then, the conclusion is false though the premisses are true. Thus:
Some odd numbers are prime,
Every odd number has for its square a number not even nor prime;
Hence, some number not even is not odd.
104. Let us enclose the description of a class in square brackets to denote the number of individuals in it. Then the premisses of the above may be arithmetically stated thus:
[x·y] > 0
[x] ≦ [ȳ·z̄]
Developing the last, we get
[x·y·z] + [x·y·z̄] + [x·ȳ·z] + [x·ȳ·z̄] ≦ [x·ȳ·z̄] + [x̄·ȳ·z̄]
Cancelling [x·ȳ·z̄], we have
[x·y·z] + [x·y·z̄] + [x·ȳ·z] ≦ [x̄·ȳ·z̄]
Developing the first premiss
[x·y·z] + [x·y·z̄] > 0.
It thus follows, not only that
[x̄·z̄] > 0
but even that, throwing aside Y's, there are more non-X's not Z's than there are X's that are Z's. But the fallacy lies in assuming the Simple Simon proposition that every part is less than its whole. That is, because the odd squares are no fewer than all the odd numbers, we quietly reason as if they were more than a part of odd numbers; so that after taking away alike from odd squares and from odd numbers the odd primes, we should necessarily have as many odd squares left over as we have odd numbers. Of collections not enumerable it is not generally true that the part is less than the whole. Every integer has a square; and thus there are as many squares as there are integers; although the squares form but a part of all the integers.
Take this example:
Every woman marries a man,
For every man there is a woman;
∴Every man is married to a woman.
The necessity of this plainly arises from the fact that after every woman has got a husband, the collection of men is exhausted. To say this, is to imply that for every quantitative relation it would have a maximum, that is, a last reached, in any order of running it through. . . .
105. The commonest sort of paralogism by far among thoughtful persons consists in reasoning as if collections were enumerable which are, in fact, inenumerable. How often do we hear one, speaking of objects in a linear series, say there must be a first or must be a last! Logic lends no color to such ideas; but, on the contrary, shows them to be pure assumptions. In metaphysics, particularly, it is frequently argued that something is analyzable into a series — by pure abstract reasoning — and then because "there must be a first" some consequence truly startling follows. Years of experience bring us to expect, as a matter of course, some fallacy, big or little, in every demonstration which seems to advance knowledge very much.
106. De Morgan's syllogism of transposed quantity does not seem very clearly or accurately to set forth precisely what the nature of the reasoning specially applicable to enumerable collections is. What does precisely describe it is, that in whatever order you pass, one by one, through the collection, you come to a last unit. But let us logically analyze this. Here there is a relation of the later-taken to the earlier-taken. The earlier is taken at a time at which the later is not taken. If l signify "taken at a time," then "taken at a time at which was not taken" is written
ll̄̆.
We see at once that this running through the collection is only a specialized way of saying that we have to do with a quantitative relation, a way of expressing it which brings in the irrelevant idea of time. The better statement is that, in reference to every quantitative relation, the enumerable collection has a last. From this it quite obviously follows that there is also a first, and that every superior of anything is next superior of something, and so also with the inferior. Another form of definition of the enumerable collection is, to say that it is a collection any part of which is less than the whole. That is, given a class, the b's, such that
∞ ⤙ b̄̆†a,
or every b is a, while
∞ ⤙ ăb̄,
or some a is not b; if, further, k is such a relative that
kbk ⤙ 1,
then
∞ ⤙ ă(k̄̆†b̄).
This is a good statement of the kind of inference peculiar to enumerable classes. It has three premisses, involving two class terms and a relative term; and it reposes directly upon the axiom that an enumerable part is less than the whole. One of the three premisses is implicitly assumed but not stated by De Morgan; the relative is his "for every," and one of his three terms is superfluous. Thus he puts the argument about the checks into form as follows: †1
"For every memorandum of a purchase a countercheque is a transaction involving the drawing of a cheque,
"Some purchases are not transactions involving the drawing of checks;
"Therefore, some countercheques are not memoranda of purchases."
But I should put it in form as follows:
Some payment for purchase was not a check,
Every payment by purchase is told off against a check;
No two payments by purchase are told against the same check;
∴ Some checks are not payments by purchase.
That is, we prove the checks are not a part of the payments by purchase, because they are not less than the payments by purchase; and it is assumed they were enumerable. If they ran on endlessly, each payment by purchase might be told off against a check of a subsequent day, the purchases increasing in number day by day.
§4. Linear Sequences
107. The second, or middling, grade of multitude is that of collections which have different attributes for different quantitative collections; namely, for some such relations, every member of the class superior to another member is next superior to some member, definitely designatable, while for other quantitative relations it is not so. I undertake to show that there is always some quantitative relation for which (1) the class has a minimum but no maximum, (2) for which every member of the class that is superior to another is next superior to some other, (3) and for which the partial class consisting of any two members of the class we are speaking of, together with all that are superior to one of these two members but inferior to the other, is enumerable. Let us begin by thinking of a member of this class, say ax. Then, considering a quantitative relation in which every a superior to an a is next superior to an a, let us think of that to which ax is next superior. Then, think of that to which the last is next superior. Then consider a partial class to all of which ax is superior, and the next inferior of each member of which is also included under it, so that either there is a minimum, which is not superior to any member of the class, or else, if ay is any member of the class to which ax is superior, and the a's at once inferior to ax and superior to ay are enumerable, it follows that ay is a member of the partial class. For if not, of all the a's superior to ay and inferior to ax, a part belongs to the partial class, and this part of an enumerable collection, being itself (as such) enumerable, must have a minimum. But by the definition of the partial class, whatever is next inferior to any member of it also belongs to it. To this partial class, then, belongs every a inferior to ax, so long as between it and az, the collection of a's is enumerable. We do not know that there is an a next superior to ax. But we define a second partial class as containing the a next superior to ax, if there be any, and as containing nothing else, except that it contains the a next superior to any a that it contains. Then, it will either contain all the a's superior to ax up to some maximum, which need not be the maximum of all the a's, but which has no a next superior to it, or, in the absence of such a maximum, it will contain all the a's up to and beyond any a superior to ax, but such that the a's inferior to it and superior to ax form an enumerable collection. The proof of this (so plain that it hardly needs statement) is as follows: if this be not the case let az be an a superior to ax and such that the a's inferior to az but superior to ax form an enumerable multitude. Then, those of those which belong to the second partial class, being part of an enumerable collection. are themselves enumerable. Hence, they have a maximum, contrary to the hypothesis. Taking the first and second partial classes together, I propose to call such a series of a's a linear sequence. I will repeat its characteristics:
1. It contains ax.
2. It contains every a inferior to ax and identical with or superior to ay, no matter what ay may be, so long as it is inferior to ax, and so long as the a's superior to ay and inferior to az form an enumerable collection.
3. It contains every a superior to ax and identical with or inferior to az, no matter what az, may be, so long as it is superior to ax, and so long as the a's inferior to az and superior to ax form an enumerable collection.
4. It has no minimum unless that minimum be the minimum of all the a's.
5. It has no maximum unless that maximum be an a which has no a next superior to it.
6. Unless the linear series happens to have a minimum and a maximum, it is itself an inenumerable collection of a's.
108. Having formed this linear sequence, if there be any a's not included in it, let a'x be one of them. We then proceed to form a second linear sequence in which a'x takes the place of ax. If, after that, there still be a's not included in the linear sequences already formed we proceed to form a next succeeding linear sequence, and so on indefinitely. The multitude of linear sequences may be inenumerable; but as necessary consequences of the rule for the formation of these sequences, the following propositions hold.
First, The linear sequences are formed successively. If we take
t
to signify "already formed at a time —", then
t̄t̆ ⤙ t̄†t̆
that is "what is not yet formed at some time at which X was already formed," is included under "formed only at times at which X was already formed." Moreover
That is, of two linear sequences not the same one was formed earlier than the other.
Second, None of the linear sequences was t̄t̆ to the first.
Third, Every sequence t̄t̆, that is formed subsequent to another, was formed on the occasion of its having been found that some a's were left over not included in the previous sequences, and thus was not t̄t̆t̄t̆, or was formed next subsequent to some other.
Fourth, All the sequences formed previous to a given sequence, have a first and last, and are an enumerable collection.
109. It is well to remark, as a matter of language, that whenever a quantitative relation is applied to a class which has for that relation a minimum, and every member of the class superior to another in respect to this relation is next superior to some other, and the partial class consisting of all inferior to any given member is enumerable, then we can conveniently speak of the relationship as constituting an arithmoidal order in which the individuals are taken, the next superior being said to come next after, etc.
110. I propose now to show that all the a's can be embraced in such a serial order. But for this purpose, I must first establish a preliminary arithmoidal order in each of the linear sequences. The first sequence may have both a minimum and a maximum, and if so, it is enumerable. If it has a minimum but no maximum, the arithmoidal order will already exist, the minimum being the first. In every sequence which has a maximum, the arithmoidal order is established by simply considering the converse of the quantitative relation for which that maximum is a maximum. It remains only to establish an arithmoidal order in each of the sequences which has neither minimum nor maximum. This we do by taking arbitrarily any a of the sequence as first of the series, and for the one next after it, the a to which it is next superior, and thereafter the following rule is to be used; next after any a, as aw, which is inferior to the a next preceding it, which we may call av, is to be taken the a next superior to av; but next after any a, as au, which is superior to the a next preceding it, which we may call uw, is to be taken the a next inferior to uw. The demonstration that this reduces the sequence to such a series is so easy that it may be omitted. We then take all the a's together in the following order: first, we take the whole of the first sequence if it is enumerable; next, we take the first a of the first inenumerable series; next, after any a of any inenumerable series we take the first a not already taken of the next inenumerable series, unless the last taken were the first of its series, when next after it we take the first not already taken of the first inenumerable series. The demonstration that this has the desired effect is sufficiently easy to be left to the student.
Such an arithmoidal series is just like the series of positive whole numbers. I call it with reference to its grade of multitude, dinumerable. That is, it corresponds one to one to the numbers, yet the count of it cannot be completed. To such a series applies the kind of reasoning called by me the Fermatian inference. This consists in proving a proposition to be true of such a series, because otherwise it must be false of an enumerable collection, such falsity, by reasoning on the principle of the part being less than the whole, being shown to be impossible. Fermat himself called it indefinite descent. He states his "manière de demonstrer," which he calls "une route tout à fait singulière" as consisting in showing that if the proposition to be proved were false of any number, it would be false of some smaller number. This statement shows a good comprehension of its nature. †1
111. If we take all the whole numbers and write opposite to each the same figures in inverse order with a decimal point before them — as, opposite 1894, for example, .4981 — and then arrange the numbers in the order of these decimal fractions, we shall have established a quantitative relation according to which no number is next superior or next inferior to any other. A story is told of a bar of tin which being sent into Russia in the depths of winter, arrived in good order only that every atom had broken away from every other. If this tale did not serve to put money in somebody's pocket, it at least affords a pretty simile of the condition of the numbers when looked upon from that below-zero point of view. To bind them together after they are in their new order would require a multitude of new units inexpressibly more numerous relative to these numbers than the totality of them is to one.
112. If from the entire series of integer numbers, ranged in regular order, we imagine none, certain ones, or all to be omitted, we have what we may call a broken series, and the multitude of the entire collection of all such broken series possible is so great that they cannot be arranged by means of any quantitative relation so that whatever one is superior to another is next superior to some one. The proof which I offer of this is at bottom not mine. It seems to me sound, and if so is wonderful. In order to show that those broken series cannot themselves be arranged in an arithmoidal order, let us first arrange them in any quantitative order. This is easy, for each number may represent a place of decimals in the binary system of numeration, 1 the 1/2 place, 2 the 1/23 place, 3 the 1/23 place, and n the 1/2n place. The absence of a number being represented by zero, and its presence by 1, each series is represented by a binarial fraction, and these may be arranged in the order of their values. (Of course, the series could not be represented by integer numbers by reflection from the binarial point, because so they would all be infinite.) Now the question is whether the series of whole numbers can in any way whatever be made to correspond to these fractions. And in order that the matter may appear in a clearer light let us suppose that parallel to the series of infinite binarial fractions is ranged the entire series of values of rational fractions between 0 and 1, expressed in the same notation and set down in the same order. Let us first take a mode of correspondence which obviously will not fulfill the purpose, but which will serve to show the difference between such a series as that of the rational fractions and the series with which we are dealing. Suppose that the numbers correspond to the fractions in the order of their simplicity. Thus our first two fractions (I won't take the trouble to write them in binary notation) are:
| 1/3 .3333333333 | 1/2 0.5000000000; |
| 2/5 .4000000000 | 3/7 0.4285742857; |
| 7/17 .4117647059 | 5/12 0.4166666667; |
| 12/29 .4137931034 | 17/41 0.4146341463; |
| 41/99 .4141414141 | 29/70 0.4142857143; |
| 70/169 .4142011834 | 99/239 0.4142259414. |
All these are found in both parallel rows; but they are converging toward
0.41421356
or √2-1 which is not a rational fraction.
Now the fact that in this case the numbers happened to be rational fractions had nothing to do with the result. It is plain that in every case, when between two values we insert two, and between those two, two more again, and so on indefinitely, there remains a limit which is never reached; and the multitude which includes all such limits cannot be made to correspond, one to one, to any dinumerable collection.
§5. The Method of Limits
113. Let us settle the terminology as shown in this diagram
The relation of the Innumerable to the Dinumerable is analogous to that of the Dinumerable to the Enumerable. Dinumerable is the multitude of enumerable numbers; innumerable is the multitude of dinumerable series. The dinumerable follows after the enumerable; but so closely after that as soon as you have passed all that is enumerable you have passed the dinumerable; so that we rightly reason such-and-such must be the character of the dinumerable, for if not there must be an enumerable which wants this character. In like manner the innumerable lies beyond the dinumerable; it is its limit; but it lies so closely beyond that we rightly reason, such-and-such must be the character of the innumerable; for if not, there must be a gap between this character and that of the dinumerable.
All reasoning about the Innumerable derives its force from the conception of a limit. We therefore have to study this conception. But two or three prolegomena are called for.
114. The idea that there can be any vigorous and productive thought upon any great subject without reasoning like that of the differential calculus is a futile and pernicious idea. Some newspapers maintain that all doctrines involving such reasoning ought to be struck out of political economy because that science is of no service unless everybody, or the great majority of voters, individually comprehend it and assent to its reasonings. I do not observe that it is a fact that voters are such asses as to insist upon thinking they personally comprehend the effects of tariff-laws, etc. But whether they be so or not, it is certain that the ratio of the circumference to the diameter is 3.1415926535897932384626433832795028841971694 . . . whether the reasoning that proves it is hard or easy. That I feel sure of, although I personally have not verified the above figures; and if I had, I should not feel perceptibly more sure of the matter than I am. Certainly, if on attempting to verify them I got a slightly different result, I should feel pretty sure it was I who had committed an error. But whether people be wise or foolish, it remains that there is no possible way of establishing the true doctrines of political economy except by reasonings about limits, that is, reasoning essentially the same as that of the differential calculus. (I do not know why I should hesitate to say that the journal which I have particularly in mind is the New York Evening Post, incontestably one of the very best newspapers in the world, and especially remarkable for the sagacity of its judgments upon all questions of public policy.)
115. The reasoning of Ricardo about rent is this. †1 When competition is unrestrained by combination, producers will carry production to the limit at which it ceases to be profitable. Thus, a man will put fertilizers on his land, until the point is reached where, were he to add the least bit more, his little increased production would no more than just pay the increased expense. Every piece of land will be treated in this way, and every grade of land will be used down to the limit of the land upon which the product can just barely pay.
The whole reasoning of political economy proceeds in this fashion. If we put an import duty upon any article, the price to the consumer cannot be raised by the full amount of the tax. For the price before the imposition was such as to sell a certain amount. Now, if the price is raised, less can be sold. If less can be sold, less will be produced. But production will only be diminished by the producer getting a less price; and it is this less price plus the duty that the consumer pays. Of course, we must understand by the duty, not merely what goes to the government, but what has to be paid in consequence to brokers, bankers, and increased expenses of all kinds caused by the change of the law. Looking at the matter from this point of view (and abstracting from other considerations) the best articles on which to levy duties are those upon the production of which our demand is so influential that a small decrease in the demand will cause a relatively large fall in the price. †P1
116. As another preliminary to the analysis of the conception of Limit, I now pass to a widely different topic. The student has not failed to remark how much I have insisted upon balance and symmetry in logic. It is a great point in the art of reasoning; although I do not know that one could say that logic requires it. As long ago as 1867 I spoke of a trivium of formal sciences of symbols in general. "The first," I said, "would treat of the formal conditions of symbols having meaning, and this might be called formal grammar; the second, logic, would treat of the formal conditions of the truth of symbols; and the third would treat of the formal conditions of the force of symbols, or their power of appealing to a mind, and this might be called formal rhetoric." †P1 It would be a mistake, in my opinion, to hold the last to be a matter of psychology. That which needs no further premisses for its support than the universal data of experience that we cannot suppose a man not to know and yet to be making inquiries, that I do not think can advantageously be thrown in with observational science. Each of these kinds of science is strong where the other is weak; and hence it is well to discriminate between them. Now, the Grundsatz of Formal Rhetoric is that an idea should be presented in a unitary, comprehensive, systematic shape. Hence it is that many a diagram which is intricate and incomprehensible by reason of the multitude of its lines is instantly rendered clear and simple by the addition of more lines, these additional lines being such as to show that those that were there first were merely parts of a unitary system. The mathematician knows this well. We have seen what endless difficulties there are with "some's" and "all's". The mathematician almost altogether frees himself from "some's"; for wherever something outlying and exceptional occurs, he enlarges his system so as to make it regular. I repeat that this is the prime principle of the rhetoric of self-communing. Nobody who neglects it can attain any great success in thinking.
117. The innumerable appears in two different shapes. In the first place, if we append to the entire series of finite integral numbers, which is a dinumerable collection, all the infinite numbers, we obtain an innumerable collection. Or, if we take the series of rational fractions, also a dinumerable collection, and add to them the limits of all infinite series of such fractions, then again we obtain an innumerable collection. In this latter case, each instance taken from the innumerable collection is a limit which may be passed through. This latter is a more balanced conception than the other; but the mathematician reduces the other to it by conceiving, that in the former case also, after passing through infinity as a mere point, we pass into a new region — a new world. We pass off, for example, in a straight line parallel to the earth's axis northwardly: after passing through infinity we pass into an imaginary region from which after an infinite passage we re-emerge into our space at the extreme south. Or, it may be that this imaginary world reduces to nothing and that the points at infinity north and south coincide. This is the way the mathematician supplements facts in the interest of formal rhetoric. Of course, in doing so he has to take care not to misrepresent the real world; but his ideal addition to it may have any properties that simplicity dictates. This is an immense engine of thought in mathematics. It affords a little difficulty to the mind at first presentation; but that passes away very soon, and then it is found to be greatly in the interest of comprehensibility. Every mathematician will tell you this; if you are not already aware of it. But even among mathematicians there is a trace of that human weakness, the stupidity of adhering to what ought to be obsolete; and consequently the idea that infinity is something to pass through has not been everywhere carried out.
118. In many mathematical treatises the limit is defined as a point that can "never" be reached. This is a violation not merely of formal rhetoric but of formal grammar. True, in the world of real experience, "never" has at least an approximate meaning. But in the Platonic world of pure forms with which mathematics is always dealing, "never" can only mean "not consistently with —." To say that a point can never be reached is to say that it cannot be reached consistently with —, and has no meaning until the blank is filled up. And thereupon, the mathematical and balanced conception must be that the point is instantly passed through. The metaphysicians have in this instance been clearer than the mathematicians — and that upon a point of mathematics; for they have always declared that a limit was inconceivable without a region beyond it.
I understand that Jordan has rewritten the first volume of his Cours d'analyse. I have not seen this new edition (for all my life my studies have been cruelly hampered by my inability to procure necessary books), but I can guess to some extent what the character of it will be; and it no doubt contains much, most pertinent to the subject now under our attention. It was, I presume, this work which suggested to Klein a remark which he makes in his Evanston Colloquium, to the effect that there is a distinction between the naïve and the refined geometrical intuition. "In imagining a line," he says, "we do not picture to ourselves length without breadth, but a strip of a certain width. Now such a strip has, of course, always a tangent; i.e., we can always imagine a straight strip having a small portion (element) in common with the curved strip." †1 The psychological remark seems to me incorrect. I, for my individual part, imagine a curve (even of an odd degree, which I convert into an even degree by doubling it, or by crossing it by a line) as the boundary between two regions pink and bluish grey; and I do not think I imagine the line as a strip. But it is of little consequence what individual ways of imagining may be. Klein's naïve view has a real importance far greater than his adjective imports, at which I have hinted in the Century Dictionary, under Limits, Doctrine of, where I say that this doctrine "should be understood to rest upon the general principle that every proposition must be interpreted as referring to a possible experience." †P1 What I mean is that absolute exactitude cannot be revealed by experience, and therefore every boundary of a figure which is to represent a possible experience ought to be blurred. If this is the case, it is both needless and useless to talk of infinitesimals. Still thought of this inexact kind (I mean upon these essentially inexact premisses) will be found much more intricate and difficult than the exact doctrine.
119. To define a limit, mathematicians usually write
xn,
where x1, x2, x3, etc. are supposed to successively approximate toward a value. Then they say that if after, perhaps, some scattering values, the successive xn's at length come nearer and nearer to a constant which they indefinitely approach but never reach, that quantity is the limit. By saying they never reach it, they mean that as the n of xn passes through infinity, xn passes through the limit. This n = ∞ of course marks the point at which the collection which n measures becomes dinumerable. At that point xn ceases to vary with n; else the value would be indeterminate.
120. I insert here a few remarks. The dinumerable is to the innumerable as logarithmic infinity is to ordinary infinity. The analogy may be traced in two ways; first the number of numbers expressible by n decimal points is, of course, bn where b is the base of the system of numeration; but the innumerable is the number of numbers expressible by dinumerable decimal points. In the second place, the innumerable is not only dinumerably more than the dinumerable but is innumerably more.
§6. The Continuum
121. It may be asked whether there be not a higher degree of multitude than that of the points upon a line. At first sight, the points on a surface seem to be more; but they are not so. For points on surfaces can be discriminated by two coördinates with values running to a dinumerable multitude of decimal places. Now two such numbers or any enumerable multitude of them can be expressed by one series of numbers. Thus to express two, write a number such that the succession of figures in the odd places of decimals gives one coördinate, and those in the even places, the other. Thus,
u = 32.174118529821685238548599709435 . . . . will mean
x = 3.141592653589793 . . .
y = 2.718281828459045 . . .
This method would break down if the number of dimensions were dinumerable; but even then another method could be found. But if the number of dimensions were innumerable, it is difficult to say without more study than I have given, how to proceed. The idea of space with innumerable dimensions does not, at first blush, at least, strike one as presenting great difficulty.
But if bn when n is dinumerable gives a new grade of multitude, we might expect that when n was innumerable, a still higher grade would be given.
Yet, on the other hand, looking at the matter from the point of view of the original definitions given above, the three classes of multitude seem to form a closed system. Still, nothing in those definitions prevents there being many grades of multiplicity in the third class. I leave the question open, while inclining to the belief that there are such grades. †1 Cantor's theory of manifolds appears to me to present certain difficulties; but I think they may be removed.
Let us now consider what is meant by saying that a line, for example, is continuous. The multitude of points, or limiting values of approximations upon it, is of course innumerable. But that does not make it continuous. Kant †2 defined its continuity as consisting in this, that between any two points upon it there are points. This is true, but manifestly insufficient, since it holds of the series of rational fractions, the multitude of which is only dinumerable. Indeed, Kant's definition applies if from such a series any two, together with all that are intermediate, be cut away; although in that case a finite gap is made. I have termed the property of infinite intermediety, or divisibility, the Kanticity of a series. It is one of the defining characters of a continuum. We had better define it in terms of the algebra of relatives. Be it remembered that continuity is not an affair of multiplicity simply (though nothing but an innumerable multitude can be continuous) but is an affair of arrangement also. We are therefore to say not merely that there can be a quantitative relation but that there is such, with reference to which the collection is continuous. Let ll̄̆ denote this relation. Then, as quantitative, this has, as we have seen, †1 these properties:
ll̄̆ ⤙ l†l̄̆,
and
Then the property of Kanticity consists in this:
ll̄̆ ⤙ l1̄̆ ll̄̆.
122. To complete the definition of a continuum, the a's, we require the following property. Namely, if there be a class of b's included among the a's but all inferior to a certain a, that is, if
b ⤙ a,
1 ⤙ ă(ll̄̆†b̄);
and if further there be for each b another next superior to it; that is,
1 ⤙ b̄̆{ll̄̆·[l̄†l̆†(b̄ l̄†l̆)]}†b,
l̄†l̆)]}†b,
then there is an a next superior to all the b's. That is,
1 ⤙ ă{(ll̄̆†b̄)·[l̄†l̆†(l̄†l̆)b]}.
I call this the Aristotelicity of the series, because Aristotle seems to have had it obscurely in mind in his definition of a continuum as that whose parts have a common limit. †2
123.  If we consider a line (which, for rhetoric's sake, we will consider as returning into itself, though if it did not, it would give no difficulty further than an intolerably tedious complexity) it consists in a connection of points, such that by virtue of it, if any two points, A and ♈ , be taken on that line, the points are divided into two parts, say the a0 and the a∞, such that a certain continuous quantitative relation, say l0, subsists between all the a0's having A for minimum and ♈ for maximum, and another continuous quantitative relation, say l∞, subsists between all the a∞'s having the same maximum and minimum. The student is invited to state this in algebraic form using Π's, Σ's, and indices. He begins, for example
If we consider a line (which, for rhetoric's sake, we will consider as returning into itself, though if it did not, it would give no difficulty further than an intolerably tedious complexity) it consists in a connection of points, such that by virtue of it, if any two points, A and ♈ , be taken on that line, the points are divided into two parts, say the a0 and the a∞, such that a certain continuous quantitative relation, say l0, subsists between all the a0's having A for minimum and ♈ for maximum, and another continuous quantitative relation, say l∞, subsists between all the a∞'s having the same maximum and minimum. The student is invited to state this in algebraic form using Π's, Σ's, and indices. He begins, for example
ΣiΠjΠk Āj Āk
Āk qij·q̄ik
qij·q̄ik q̄ij·qik
q̄ij·qik l0jk
l0jk l0kj
l0kj ∞jk
∞jk l∞kj.
l∞kj.
To this I wish to add something, which seems to require a preliminary remark. There are certain quantitative relations between the points such that if one of them were to govern an arrangement of the points in space, it would derange their connection in a line, in this sense, that it would cause some four points which are connected in the cyclical order PQRS (=PSRQ) to be brought in to one of the two orders PQSR (=PRSQ) or PSQR (=PRQS). We will call such a relation, for short, incompatible. Of course, there is nothing to prevent its existing; only the points cannot be arranged according to this order and remain in their order in the line. I now say that by no compatible continuous quantitative order can we pass from any a0 to any a∞, without passing through A or Ω . The student will do well to express this in terms of the algebra. Of course this statement requires modification in case the line forks. But for the purposes of logic it does not seem necessary to examine such details.
124. Pass we now to the study of the Surface. It is here that the mathematical conception of a "spread" — as Clifford calls it in insular but expressive language — at length displays itself. For an example of a surface, think of something irregularly round — multiple-connected surfaces complicate the subject, without advantage. They are easily taken into account later and the modifications they require made. A surface contains an innumerable multitude of lines. Let one of these — a complete oval — be marked upon it. Then the connection of points is such that this line separates those that do not lie upon it into two classes, such that it is impossible to pass from any point of one class to any point of the other by a compatible continuous quantitative order without passing through some point of the line. This is, however, perhaps not quite clear. Let us endeavor to make a better statement. Upon the oval take two points A and Ω . Then by virtue of the connection of points on the surface there is an innumerable series of continuous quantitative orders, each beginning at A and ending at Ω . Two of these, signified by the relative terms l0 and l∞, follow the two parts of the oval. These orders are such that no two of them embrace the same point, except the initial and final points which are common to them all. And all other lines (or compatible continuous quantitative orders), twice cutting the oval, cut these different lines in the same order, say l0 . . ln . . l∞ . . ln . . . l0 . . . Every point on the surface lies on one of these lines.
§7. The Immediate Neighborhood
125. I wish to remark that it is a serious fault in the ordinary treatment of the fundamentals of geometry that attention is not paid to the distinction between the two sides of points on a line, lines on a surface, and surfaces in space. This is why certain theorems indubitably true are so difficult of formal proof. It is that a part of the fundamental properties of space have no expression among the Postulates of Geometry.
I think that I have thus described the nature of the connection of points upon the surface — and nothing need be added.
But there are three very important ideas I have left undefined. I mean those of the simplest line (straight line on a plane, great circle on a sphere, perhaps the geodetic line on other surfaces), the immediate neighborhood, and measurement. I have also imaginary quantity still to consider.
The easiest of these ideas seems to be that of the immediate neighborhood. It supposes that we recognize that every region stands in relation to a certain scale of quantity. We do not yet assign its quantity but we are able to say whether it is connected with an enumerable, a dinumerable, or an innumerable multitude. Two regions which are connected with quantities of the same class are said to be about alike. Suppose, then, we have a region about like the whole surface, or about like some region which we take as a standard. Suppose a thunder-bolt rends this into two parts about alike, a crack separating them. Suppose a second thunderbolt similarly rends both parts; and each successive thunderbolt rends all the parts the last left into two new parts about alike. Suppose these thunderbolts to follow at the completion of each rational fraction of a minute. Then, at the end of the minute, the region will be rent into innumerable parts about alike. These parts are neighborhoods or infinitesimals.
126. It will at once be objected that there is no reason to suppose that this operation would leave any parts at all, or if it did there is no reason to suppose they would be surfaces rather than angels, or oranges, or precessions of the equinoxes; for the only reason for thinking they remained of the same genus is that no one thunderbolt would change them. Reasoning from that premiss, however, would be a Fermatian inference, and would, as such, only hold good for the dinumerable.
But the reply is that there is no need of calling in the Fermatian inference. The minute of thunderbolts does not differ from any other minute, as far as the character of the surface goes. The parts have been moved a little, but all their mutual relations are undisturbed. Even if the operation broke it up into single points, which is an unfounded proposition, still all the cracks that have been made in no wise alter the relations of the points to one another. The space the region occupies, though interfiltrated through with another space, remains the same, and the relations of its parts the same. If this conception is too difficult, imagine that the thunderbolts do not rend the regions, but only cause a mind to imagine them rent.
It would, however, be quite out of order to consider the question of whether these parts are single points or what their composition may be, until it first be fully admitted that the logical division of the region into innumerable parts is logically possible. But there is no room for dispute here. It has been irrefragably demonstrated that the points of a line, and a fortiori of a surface, are innumerable. Now, as no two coincide, there is nothing in logic to prevent their being drawn asunder. My definition of a continuum only prescribes that, after every innumerable series of points, there shall be a next following point, and does not forbid this to follow at the interval of a mile. That, therefore, certainly permits cracks everywhere; for there is no ordinal place in the series where such a limit point is not inserted. But if anybody thinks my definition is in error here, still it will not be maintained that that definition involves any contradiction. Hence, there is no contradiction in the separation into parts, even if I am wrong in saying that it involves no breach of continuity. There is no contradiction involved in breaking the region anywhere. But perhaps it may be said, the contradiction lies, not in breaking it anywhere, nor in breaking it into as many parts as it has points, but that the idea of an innumerable multitude involves a contradiction. That it does not can be formally demonstrated by second-intentional logic; but that part of this book having been excised, it is necessary to find other arguments. There is no difficulty about the existence of Π, and therefore none in the existence of incommensurable limits. There is no more difficulty about the existence of any one number not accurately expressible in a finite number of decimals than in any other. Therefore, there is no logical contradiction in supposing all numbers to which decimals can indefinitely approximate to exist, i.e., as all the objects of mathematics exist, as abstract hypotheses. Besides, that the innumerable multitudes are logically possible is shown by the fact that many propositions (namely all that are true of the dinumerable but not of the numerable) cannot be demonstrated in a way which will stand logical examination unless it be expressly introduced as a premiss that a given multitude is numerable. Now a logically necessary proposition is of no avail as a premiss. On the whole then, there is nothing in logic to prevent a region from being divided into innumerable parts about alike.
Now I say that each of those parts contains innumerable points. For if that were not the case each of these parts could be so arranged that every point had another next after it; and, since a continuum has no molecular constitution, the divisions could everywhere be made between points having other points next them; and so, after rearranging the parts (no matter how the continuity might be broken up) all the points would have points next after them. But this is contrary to the fact that the points are innumerable. Besides, going back to the unanalyzed idea of continuity, it is evident that in a continuum the points are so connected that every part, irrespective of its magnitude, contains innumerable points. It may be objected that the single points are parts. But that is not properly true. The single points are parts of the collection; but they cannot be broken off by a division of parts unless they are on the outer boundary of a region, or unless they are not continuous with the rest. They can be extracted from the middle; but doing this breaks the continuity. Thus the incommensurable numbers taken by themselves do not form a continuum.
127.  A drop of ink has fallen upon the paper and I have walled it round. Now every point of the area within the walls is either black or white; and no point is both black and white. That is plain. The black is, however, all in one spot or blot; it is within bounds. There is a line of demarcation between the black and the white. Now I ask about the points of this line, are they black or white? Why one more than the other? Are they (A) both black and white or (B) neither black nor white? Why A more than B, or B more than A? It is certainly true,
A drop of ink has fallen upon the paper and I have walled it round. Now every point of the area within the walls is either black or white; and no point is both black and white. That is plain. The black is, however, all in one spot or blot; it is within bounds. There is a line of demarcation between the black and the white. Now I ask about the points of this line, are they black or white? Why one more than the other? Are they (A) both black and white or (B) neither black nor white? Why A more than B, or B more than A? It is certainly true,
First, that every point of the area is either black or white,
Second, that no point is both black and white,
Third, that the points of the boundary are no more white than black, and no more black than white.
The logical conclusion from these three propositions is that the points of the boundary do not exist. That is, they do not exist in such a sense as to have entirely determinate characters attributed to them for such reasons as have operated to produce the above premisses. This leaves us to reflect that it is only as they are connected together into a continuous surface that the points are colored; taken singly, they have no color, and are neither black nor white, none of them. Let us then try putting "neighboring part" for point. Every part of the surface is either black or white. No part is both black and white. The parts on the boundary are no more white than black, and no more black than white. The conclusion is that the parts near the boundary are half black and half white. This, however (owing to the curvature of the boundary), is not exactly true unless we mean the parts in the immediate neighborhood of the boundary. These are the parts we have described. They are the parts which must be considered if we attempt to state the properties at precise points of a surface, these points being considered, as they must be, in their connection of continuity.
One begins to see that the phrase "immediate neighborhood," which at first blush strikes one as almost a contradiction in terms, is, after all, a very happy one.
What is the velocity of a particle at any instant? I answer it is the ratio of space traversed to time of traversing, in the moment, or time in the immediate neighborhood, of that instant, or point of time. Some logicians object to this. They say that the velocity means nothing but the limiting value of the ratio of the space to the time when the time is indefinitely diminished. But they say they use the expression "immediate neighborhood" to mean nothing more than that, as a convenience of language. Sometimes we meet with an assertion difficult to refute because it involves several difficult logical blunders. The position just stated is an example of this. People who talk in this way do not see that what they say is a justification of the idea of a part such as the whole contains an innumerable multitude of. I do not yet say "immeasurably small," because we have not yet studied the conception of measurement. These people do not seem to have analyzed the conception of a "meaning," †1 which is, in its primary acceptation, the translation of a sign into another system of signs, and which, in the acceptation here applicable, is a second assertion from which all that follows from the first assertion equally follows, and vice versa. It is true that, when we find with reference to a continuous motion that something would be true at the limit of a dinumerable series, it follows this is true for the part about the point considered. . . . This is as much as to say that the one assertion "means" the other. But do these people mean to say that when I think of a particle as having a velocity, I can only think, or that it is convenient to think, simply that at different times it is stationed at different points? Do they mean to say I have no direct, clear icon of a movement? If so, they are shutting their eyes to the plain truth. Remember it is by icons only that we really reason, and abstract statements are valueless in reasoning except so far as they aid us to construct diagrams. The sectaries of the opinion I am combating seem, on the contrary, to suppose that reasoning is performed with abstract "judgments," and that an icon is of use only as enabling me to frame abstract statements as premisses.
The idea of "immediate neighborhood" is an exceedingly easy one, into which everybody is continually slipping, though he fancies it unjustifiable. Klein says of his "refined intuition" that, strictly speaking, it is not an intuition. But, speaking as strictly as that, there is no such psychological phenomenon as an intuition. †1 The strip, which he says makes the curve in the naïve intuition, makes two parallel curves with a region between. But the simple idea is that of a blurred outline, to which we all, wise and simple, append the mental note that its breadth is such that an innumerable number would be contained in any surface.
Those who, finding themselves betrayed into the use of the expression "immediate neighborhood" or something equivalent, seek to justify it by the exigencies of speech, are mistaken. It is not English grammar which forces these words upon them, but it is the very grammar of thought — formal grammar — which forces the idea upon them. The idea of supposing that they can think about motion without an image of something moving!
We must return to this subject after having considered the nature of measurement.
§8. Linear Surfaces
128. Euclid †2 defines a straight line as a line which lies evenly between its points. This is the real Greek acuteness; it is as much as to say that if a straight line be moved, its new position intersects its old one in one point at most. This is substantially the idea of all modern geometry. Legendre, †3 it is true, defined the straight line as the shortest distance between two points, as it most indubitably is. Nor do I think that it would be fair to object that this definition is metrical, that is, supposes a definition of measurement. For all kinds of measurement known make the straight line the shortest (or the longest, sometimes, if there be a longest) distance, if there be a shortest distance. But a more serious objection to Legendre's definition is that, if that be adopted, its property of two straight lines not intersecting in two places follows as a consequence; while, if Euclid's definition be adopted, there must be a separate postulate to the effect that there is a shortest distance. Thus, Euclid's definition involves a more thorough analysis of the properties of space. Legendre conceived the other way, which wraps up as much as possible in one formula, to be the best. It certainly is not so for the purposes of logic.
When instead of a plane we consider a roundish surface, it is difficult to say what sort of an oval best corresponds to a straight line. Most writers have assumed that it is the geodetic line which is the shortest (or longest) distance between its points. But they seem to have forgotten that a geodetic line on almost any surface but a perfect sphere generally intersects itself a dinumerable multitude of times. The discussion of this question would involve very difficult mathematics, quite out of place in this work.
We must, therefore, confine ourselves to the plane. Now it is evident that the definition we have adopted supposes straight lines to move about in the plane without ceasing to be straight. Hitherto, all the properties of the connection of points are such as might hold if the plane were a fluid; for though discontinuous fluid motion is conceivable, it has no place in the usual conceptions of the student of hydrokinetics. But now we propose that the straight line should move about as if it were a rigid bar. However, it is not necessary to broach the theory of elasticity, a doctrine of Satanic perplexity. We may call a straight line the path of a ray of light, or the shadow of a dark point cast from a luminous point. That is rather a pretty idea. Or going down to the roots of physics, we may define the straight line as the path of a particle, not deflected by any force. This is, so far as we can see, the origin of the importance of the straight line in the physical world. But, then, at present it is doubtful whether we are concerned at all with the physical world. We would like, if we could, to find some logical property of the straight line distinguishing it from other curves. I fear, however, there is none, if we are to leave its shortness out of account. We can perfectly well conceive of a cubic curve, such as is shown in the figure,  moving about with modifications of its shape, so as in any position to cut any other position once and once only (in real space). A mathematician will easily write down the conditions for this. Namely, the equation of the serpentine is y = 1/(x+(1/x)),
moving about with modifications of its shape, so as in any position to cut any other position once and once only (in real space). A mathematician will easily write down the conditions for this. Namely, the equation of the serpentine is y = 1/(x+(1/x)),
and that of the different cubics is
x/a + {y-(1/(x+(1/x)))}/b=1.
There is nothing in the plane geometry of the straight line which is not equally true, mutatis mutandis, of such a system of cubics.
But the intersectional properties of straight lines in a plane are not exhausted in saying that any two straight lines intersect once and once only.
129. Let us resort to our algebra of relatives. Denote unlimited straight lines by lower case italic letters. Let capitals denote points. Let Greek minuscules denote certain marks of lines. All these letters are treated as indices; but they will be written on the line.
Let aB (or any similar pair of letters) mean that the line a is considered as having the point B, which lies on it. If the point B is not on the line a, then ~(a B); but even if B be on a, it does not necessarily follow that B is regarded as belonging to the line a, and if not, again ~(a B). A point may belong to two lines, at once.
Let ab (or any similar pair of letters) signify that the line b has the mark a, the nature of which will appear in the sequel.
Let αB, etc., signify that the point B belongs to some line that has the mark α.
Let us now endeavor to sum up in a series of propositions the fundamental truths about the intersections of lines.
First proposition.
| ΠAΠBΣc | cA·cB |
Second proposition.
| ΠαΠβΣc | αc·βc, |
Third proposition.
| ΠaΠbΠCΠD | ~(aC) ~(aD) ~(aD) ~(bC) ~(bC) ~(bD) ~(bD) 1ab 1ab 1CD, 1CD, |
Fourth proposition.
| ΠαΠβΠcΠd | ~(αc) ~(αd) ~(αd) ~(βc) ~(βc) ~(βd) ~(βd) 1αβ 1αβ 1cd, 1cd, |
Fifth proposition.
| ΠAΠbΣγ | γb·γA, |
Sixth proposition.
| ΠαΠbΣC | αb·αC, |
Seventh proposition.
| ΠαΠβΠcΠD | ~(αc) ~(αD) ~(αD) ~(βc) ~(βc) ~(βD) ~(βD) cD cD 1αβ, 1αβ, |
Eighth proposition.
| ΠαΠbΠCΠD | ~(αC) ~(αD) ~(αD) ~(bC) ~(bC) ~(bD) ~(bD) αb αb 1CD, 1CD, |
Ninth proposition.
ΠαΠbΠcΠdΠE ~(αb) ~(αc)
~(αc) ~(αd)
~(αd) ~(bE)
~(bE) ~(cE)
~(cE) ~(dE)
~(dE) 1bc
1bc 1bd
1bd 1cd,
1cd,
that is, any three lines either have no common point or no common mark.
Tenth proposition.
| ΠbΠcΠdΣαΣE | αb·αc·αd bE·cE·dE †1 †P1, bE·cE·dE †1 †P1, |
130. . . . The student may object, at first blush, that the marks indicated by Greek letters have no meaning. This is a great mistake; they have precisely the meaning that is pertinent; but it is true they have no meaning in the sense of anything which particularly strikes ordinary attention. Reflect upon this. What people call an "interpretation" is a thing totally irrelevant, except that it may show by an example that no slip of logic has been committed.
131. At this point, I should like to give some account of Schubert's calculus of enumerative geometry †2, which is the most extensive application of the Boolian algebra which has ever been made, and is of manifestly high utility. But I do not feel that I could possibly condense the elementary explanations or clarify them more than Schubert has himself done in his book. He has by no means exhausted the powers of his method. There is plenty of room for new researches; but his work will stand as the classical treatise upon geometry as viewed from the standpoint of arithmetic for an indefinite future.
§9. The Logical and the Quantitative Algebra
132. Cauchy †3 first gave the correct logic of imaginaries, and very instructive it is. But the majority of writers of textbooks, who reason by the rule of thumb, do not understand it to this day. The square of the imaginary unit, i, is -1, and therefore it may be allowable to speak of i and -i as being two square roots of -1. But to speak of them as the two square roots of -1 will not do. The algebraist sets out with a single continuous quantitative relation. But when he comes to quadratics he finds himself confronted with impossible problems. He says: "I want a square root of negative unity. Now there is no such thing in the universe: clearly, then, I must import it from abroad." Let us see how one would go about to prove there is no square root of negative unity. He would reason indirectly: that is the mathematician's recipe for everything. He would say let i be this square root if there be one. Then, whether its sign be + or -, its square will have a positive sign, contrary to the hypothesis. Then the whole impossibility depends upon this, that every quantity is supposed to be positive or negative. Suppose we make i neither positive nor negative. "But there is no such thing," some rule-of-thumb man says. Really? In that respect it is just like all the other objects the mathematician deals with. They are one and all mere figments of the brain. †1 "But to say that a quantity is neither positive nor negative means nothing," objects the thumbist. I reply, the meaning of a sign is the sign it has to be translated into. Now in mathematics, which is merely tracing out the consequences of hypotheses, to say a thing has no meaning is to say it is not included in our hypothesis. In that case, all we have to do is to enlarge the hypothesis and put it in. That is your course when you have a concrete hypothesis. That was our conduct when we called a debt, negative property. But, at present, we are dealing with algebra in the abstract. The only hypothesis we make is that our letters obey the laws of algebra. If there is one of those laws which requires a quantity to be either positive or negative, find out which it is and delete it. If you have a system of laws which is self-consistent, it will not be less so when one of them is wiped out. But let us see what the laws of algebra are and how they are affected toward a quantity whose square is negative. We have,
| (1) | If x = y, then x may anywhere be substituted for y. |
| (2) | x+y = y+x. |
| (3) | x+(y+z) = (x+y) +z. |
| (4) | xy = yx. |
| (5) | x(yz) = (xy) z. |
| (6) | (x+y) z = xz+yz. |
| (7) | x+0 = x. |
| (8) | x1 = x. |
| (9) | x+∞ = ∞. |
| (10) | If x+y = x+z, either y = z or x = ∞. |
| (11) | If xy = xz, either y = z, or x = 0, or x = ∞. |
| (12) | If x>y, not y>x. |
| (13) | If x>y, then there is a quantity a such that a>0 [and] a+y = x. |
| (14) | If x>y, then x+z>y+z. |
| (15) | If x>0 and y>0, then xy>0. |
| (16) | Either x>y, or x = y, or y>x. |
| (17) | 1>0. |
It is plain that from these equations it is impossible to prove that x2<0 is not true except by the aid of one of the last six formulæ, and further that it will be requisite to consider the factors of x2. Now (15) is the only one of the last six formulæ, directly containing a product. This gives x2>0 provided x>0. Also, if 0>x, let x+ξ = 0, by (13), where ξ>0.
Then, by (6),
xξ+ξ2 = 0
But by (7),
y+0 = y,
and by (6),
(y+0)ξ = yξ+0ξ = yξ,
and by (7),
yξ+0ξ = yξ+0,
and by (10),
either 0ξ = 0 or yξ = ∞ whatever y may be.
But the last alternative is absurd; for then by (9),
y0 = y(x+ξ) = yx+yξ = yx+∞ = ∞.
But if y = 1 by (8),
y0 = 10 = 0.
Hence we should have
0 = ∞
whence by (7) and (9),
z = 0 = ∞
whatever z may be. Hence by (1),
If u>v v>u
Hence by (12), in no case is u>v. But this contradicts (17).
We have, then,
0ξ = 0.
Hence by (2) and (7),
xξ+ξ2 = 0,
But by (15),
ξ2>0.
Hence by (14),
xξ+ξ2>xξ+0.
Hence by (7),
xξ+ξ2>xξ
or,
0>xξ.
But by (6) and (4),
x(x+ξ) = x2+xξ = x0 = 0x = 0.
Hence,
x2+xξ>xξ.
Now since 0>xξ by (13) there is a quantity a such that
a>0, a+xξ = 0
Hence, by (14),
x2+xξ+a>xξ+a
Hence, finally, by (3),
x2+0>0
or by (7),
x2>0.
Hence, by (16), in every case
x2>0 or x = 0.
But it is plain that without (16) this conclusion could not be drawn, since no other of the formulæ (12)-(17) have anything to say about quantities neither greater, less, nor equal to one another.
It thus appears that we have only to strike out (16), and the quantity i such that i2 = -1, becomes perfectly possible, and perfectly conceivable, in the only clear sense of that word, namely, that we can write down
i2+1 = 0
without conflict with any formula. If we define -x by the formula
x+(-x) = 0,
then, necessarily, if i2 = -1, we have also (-i)2 = -1. Ordinary algebra assumes there is no other quantity except these two whose square equals -1. Thus, if the algebraist finds x2 = y2 he at once writes x = ±y. This is because he chooses to exclude all other square roots of -1. I will return to this point shortly. †1
133. Men are anxious to learn what the square root of negative unity means. It just means
i2+1 = 0;
precisely as -1 means
1+(-1) = 0.
The algebraic system of symbols is a calculus; that is to say, it is a language to reason in. Consequently, while it is perfectly proper to define a debt as negative property, to explain what a negative quantity is, by saying that it is what debt is to property, is to put the cart before the horse and to explain the more intelligible by the less intelligible. To say that algebra means anything else than just its own forms is to mistake an application of algebra for the meaning of it. †P1 But to this statement a proviso should be attached. If an application of algebra consists in another system of diagrams having properties analogous to those of the sixteen fundamental formulæ, or to the greater number of them, and if that other system of diagrams is a good one to reason in, and may advantageously be taken as an adjunct of the algebraic system in reasoning, then such system of diagrams should be regarded as more than a subject for the application of logic, and though it is too much to say it is the meaning of the algebra, it may be conceived as a secondary, or junior-partner meaning. Such junior interpretations are especially, the logical and the geometrical.
134. Logical algebra ought to be entirely self-developed. Quantitative algebra, on the contrary, ought to be developed as a special case of logical algebra. I do not mean that elementary teaching should set it on that basis; but that should be recognized as the fundamental philosophy of it. The seminary logicians have often seemed to think that those who study logic algebraically entertain the opinion that logic is a branch of the science of quantity. Even if they did, the error would be a trifling one; since it would be an isolated opinion, having no influence upon the main results of their studies, which are purely formal. But with the possible exception of Boole himself, whose philosophical views have not been lauded by any of his followers, none of the algebraic logicians do hold any such opinion. For my part, I consider that the business of drawing demonstrative conclusions from assumed premisses, in cases so difficult as to call for the services of a specialist, is the sole business of the mathematician. Whether this makes mathematics a branch of logic, or whether it cuts off this business from logic, is a mere question of the classification of the sciences. I adopt the latter alternative, making the business of logic to be analysis and theory of reasoning, but not the practice of it. To show how reasoning about quantity may be facilitated by considering logical interpretations, I may instance the Enumerate Geometry of Schubert, †1 which works by means of the logical calculus, and Mr. MacColl's †2 method of transposing the limits of multiple integrals, which is done by the Boolian algebra. Dr. Fabian Franklin has effected some difficult algebraical demonstrations by considering quantities as expressive of probabilities. I myself made two additions to the theory of multiple algebra by considering it as expressive of the logic of relatives. †3
135. The idea of multiplication has been widely generalized by mathematicians in the interest of the science of quantity itself. In quaternions, and more generally in all linear associative algebra, which is the same as the theory of matrices, it is not commutative. The general idea which is found in all of these is that the product of two units is the pair of units regarded as a new unit. Now there are two senses in which a "pair" may be understood, according as BA is, or is not, regarded as the same as AB. Ordinary arithmetic makes them the same. Hence, 2×3 or the pairs consisting of one unit of a set of 2, say, I, J, and another unit of a set of 3, say X, Y, Z, the pairs IX, IY, IZ, JX, JY, JZ, are the same as the pairs formed by taking a unit of the set of 3 first, followed by a unit of the set of 2. So when we say that the area of a rectangle is equal to its length multiplied by its breadth, we mean that the area consists of all the units derived from coupling a unit of length with a unit of breadth. But in the multiplication of matrices, each unit in the Pth row and Qth column, which I write P:Q, of the multiplier coupled with a unit in the Qth row and Rth column, or Q:R gives
(P:Q)(Q:R) = P:R
or a unit of the Pth row and Rth column of the multiplicand. If their order be reversed,
(Q:R)(P:Q) = 0,
unless it happens that R = P.
136. In my earlier papers on the logic of relatives I made an application of the sign of involution †1 which, I am persuaded, is less special than it seems at first sight to be. Namely, I there wrote
ls
for the lover of every servant, while ls was the lover of some servant.
l(sm) = (ls)m
or the lover of everything that is servant to a man stands to every man in the relation of lover of every servant of his.
or the lover of everything that is either woman or man is the same as the lover of every woman and, at the same time, lover of every man.
(l·b)m = lm·bm
or that which is to every man at once lover and benefactor is the same as a lover of every man who is benefactor of every man.
(e c)f = ef
c)f = ef [f]ef-1*·c1*
[f]ef-1*·c1* ([f]·([f]-1))/2·ef-2*·c2*
([f]·([f]-1))/2·ef-2*·c2* etc.
etc.
that is to say, those things each of which is to every Frenchman either emperor or conqueror consist first of the emperors of all Frenchmen; second, of a number of classes equal to the number of Frenchmen, each class consisting of all emperors of all Frenchmen but one who are at the same time conquerors of that one; third, of a number of classes equal to half the product of the number of Frenchmen by one less than the number of Frenchmen, each class consisting of every individual which is emperor of all Frenchmen but two and conqueror of those two; etc.
This makes
lm = l m1·l m2·l m3·l m4· etc.
Of course, the ordinary idea which makes of involution the iteration of an operation, is a special case under this.
Thus, quantitative algebra is only a special development of logical algebra. On the other hand, it is equally true that the Boolian algebra is nothing but the mathematics of numerical congruences having 2 for their modulus.
137. The geometrical interpretation affords great aid in reasoning, because man has, so to speak, a natural genius for geometry. Thus we see easily enough, algebraically, that
and further that
But that which is by no means obvious algebraically, but becomes obvious geometrically, is that when we plot x and y as abscissa and ordinate of rectangular coördinates and u, v as other values of the same coördinates, and the product in the same way, the angle from the axis of abscissas of the product is equal to the sum of those of the two factors. This once found out, in the geometrical way, is easily put into algebraical form. Geometry here renders a precisely similar service to that which the theory of probabilities often lends. There are several instances in which mechanical instincts have been valuable in the same way. A choice collection of such lemmas would be interesting.
§10. The Algebra of Real Quaternions
138. I now turn back to square roots of negative unity, not supposing multiplication to be commutative. That is, we do not generally have xy = yx. Suppose we have two quantities i and j, such that
i2+1 = 0
j2+1 = 0
Then it is plain that
(iji)(iji) = (ij)ii(ji) = -(ij)(ji) = -i·jj·i = ii = -1,
so that iji and jij are also square roots of negative unity.
Five cases may be studied:
| First, | iji = i |
| Second, | iji = -i |
| Third, | iji = j |
| Fourth, | iji = -j |
| Fifth, | iji = k (a third unit). |
| First Case. | iji | = i. | Then, |
| i·iji | = -ji | = ii | |
| -j | = i. |
| Second Case. | iji | = -i. | Then, |
| i·iji | = -ji | = -ii | |
| j | = i. |
| Third Case. | iji | = j. | Then, |
| ijij | = jj | = - 1 | |
| jiji = jj = - 1 |
and ij and ji are also square roots of negative unity.
iji·i = -ij = ji.
But,
(ij)i = j
i(ij) = -j,
equations that do not hold for ij = i nor for ij = j.
Nor can we put
ij = sin Θ.i+cos Θ.j
For then,
i.ij = -sin Θ+cos Θ.ij = -sinΘ+cosΘ sinΘ.i+cos2 Θ.j
and we have
cosΘ = √-1.
Let us then write
ij = k
ji = -k
Then,
ki = iji = j
ik = iij = -j
kj = ijj = -i
jk = -jji = i
This is the algebra of quaternions. †1
Fourth Case.
iji = -j. Then,
iji.i = -ij = -ji
or
ji = ij.
Hence, sincei2 = j2
(i-j)(i+j) = 0
j = ±i.
Fifth Case.
iji=k.
The multiplication cannot be commutative. We may then have four infinite series of units
| i1 = i | j1 = j | k1 = ij | l1 = ji |
| i2 = iji | j2 = jij | k2 = ijij | l2 = jiji |
| i3 = ijiji | j3 = jijij | k3 = ijijij | 13 = jijiji |
| i4 = ijijiji | j4 = jijijij | k4 = ijijijij | 14 = jijijiji |
| etc. | etc. | etc. | etc. |
Here
| in = | iln-1 = kn-1i |
| jn = | jkn-1 = ln-1j |
| imjn = | km+n-1 |
| jmin = | lm+n-1 |
It is possible to suppose these all different.
If, on the other hand, any two are equal, there are but a finite number of different units. For example, if
ijijiji = jij
then,
ijiji = jijij
And all forms of more than five letters are equal to forms of quite as few as five letters. Thus,
ijijij = jijij.j = -jiji.
139. †1 But the moment we suppose the number of linearly independent letters is finite we can reason as follows. Taking any expression, A, some power of it is a linear function of inferior powers. Hence, there is some equation
Σm(amAm)+a0 = 0.
By the theory of equations, this is resoluble into quadratic factors. One of these, then, must equal zero. Let it be
(A-s)2+t2 = 0.
Then,
((A-s)/t)2 = -1
or, every expression, upon subtraction of a real number from it, can be converted, in one way only, into a square root, of a negative number. Let us call such a square root, the vector of the first expression, and the real number subtracted, the scalar of it.
Let v2 = -1, j2 = -1, and ij = s+v,
where s is scalar, and v vector. Then it is impossible to find three real numbers, a, b, c, such that
v = a+bi+cj
For assume this equation. Then, since
| ij.j = -i, | |
| -i = sj+vj | =-c+(s+a)j+bij |
| = bs-c+ab+b2i+(s+a+bc)j. |
Whence,
b2 = -1,
and b could not be real.
Moreover, we shall have
ji = r(s-v),
where v is a real number. For write
ji = s'+v',
where s' is the scalar, and v' the vector, of ji. Let us write, too,
vv' = s''+v'',
where s'' and v'' are again the scalar and vector of vv'. Then,
ij.ji = (s+v)(s'+v') = ss'+sv'+s'v+s''+v''.
But
ij.ji = 1.
Hence,
v'' = 1-ss'-s''-sv'-s'v.
But it has just been proved that the vector of the product of two vectors is linearly independent of these vectors and of unity. Hence
v'' = 0.
That is,
sv' = 1-ss'-s''-s'v.
But it has just been shown that a quantity can be separated into a scalar and a vector part in only one way. Hence
sv' = -s'v
s'' = 1-ss'.
The former equation makes
ji = (s'/s)(s-v).
Let us next consider such an expression as
ai+bj = S+V
where S and V are the scalar and vector of the first member. Squaring the vector, we get
V2 = -N = (ai+bj-S)2 = -a2-b2+S2+abs+abs'-2aSi-2bSj +ab(1-(s'/s))v
or
ab(1-(s'/s))v = -N+a2+b2-S2-abs-abs'+2aSi+2bSj.
But since v is the vector of ij it must, as we have seen, be linearly independent of unity, i, and j. Hence the first member must vanish. But if v = 0, ij = s, whence -i = sj, contrary to hypothesis. Hence,
1-(s'/s) = 0
or
s' = s.
Whence,
s'' = 1-s2.
But s'' being the negative of the square of v is positive. Hence,
s2≦1.
We know that ai+bj cannot be a scalar; for then a quantity could in two ways be resolved into a scalar and vector part. Now
(ai+bj)2 = -a2-b2+2abs.
This must therefore be negative. For (ai+bj) = S+V, and V does not vanish. Hence
(ai+bj)2 = S2+V2+2SV;
and since, by comparison, it appears the vector part 2SV vanishes, it follows that S = 0, and the sum, or linear function, of two vectors is a vector.
The same thing is evident because S2≦1; whence
-a2-b2+2abs = -p(a+b)2-(1-p)(a-b)2,
where p = (1+s)/2 and 1-p = (1-s)/2, both of which are positive, or zero.
Let us then assume a vector j, such that
j1 = (si+j)/(√(1-s2))
j12 = (-s2-1+2s2)/(1-s2) = -1
ij1 = (-s+s+v)/(√(1-s2) = v/(√(1-s2)
j1i = -(v/(√(1-s2))
j1 = (v/(√(1-s2)) = j1ij1 = -j12i = i
(v/(√(1-s2))j1 = ij1j1 = -i
i(v/(√(1-s2)) = iij1 = -j1
(v/(√(1-s2))i = -jii = j1
(v/(√(1-s2))2 = -ij1j1i = -1
Writing j for j1 and k for v/√(1-s2) and the above formulæ define the algebra of real quaternions.
140. †1 I will now prove that it is not possible to add to this a fourth linearly independent vector. For suppose l to be such a unit vector. Write
jl = S'+V',
li = S''+V''.
Substitute for l,
l1 = S''i+S'j+l
Then,
jl1 = -S''k-S'+S'+V' = -S''k+V',
l1j = S''k-S'+S'-V' = S''k-V',
l1i = -S''-S'k+S''+V'' = -S''k+V'',
il1 = -S''+S'k+S''-V'' = S''k-V''.
Let us further assume
kl1 = S'''+V'''
Whence,
l1k = S'''-V'''.
But
l1j = -jl1 and l1i = -il1.
Hence,
kl = i.jl1 = -i.l1j = -il1.j = l1i.j = l1.ij = lk.
So,
kl1 = l1k
or,
kl1-l1k = 0
But we have seen that
kl1-l1k = S'''+V''-S'''+V''' = 2V'''.
Hence V''' = 0. Then these vectors are not linearly independent, and a fourth unit vector is impossible.
But this proof does not apply when the multitude of linearly independent expressions is endless; such algebras are nonlinear.
We thus see that even when we annul the commutative law of multiplication, there are but three linear algebras, real single algebra, ordinary imaginary algebra, and the algebra of real quaternions which obey all the other algebraic laws. The law which so limits the number is:
If xy = xz, then y = z, unless x = 0 or x = ∞.
141. In all other algebras this law fails and with it goes all semblance of importance for the inverse operation of division. †P1 The algebra of logic illustrates the vanity of that device for solving equations, which must on the contrary usually be solved by producing special known quantities by direct operations.
§11. Measurement
142. It was necessary to say something about imaginaries before coming to the subject of measurement since the modern theory of measurement (due to the researches of Cayley, Clifford, Klein, etc.) depends essentially upon imaginaries.
Let us first consider measurement in one dimension. There is a certain absurdity in talking about measurement in one dimension. This is seen in the instance of time. Suppose we only knew the flow of our inward sensations, but nothing spread into two dimensions, how could one interval of time be compared with another? Certainly, their contents might be so alike that we should judge them equivalent. But that is not shoving a scale along. It does not enable us to compare intervals unless they happen to have similar contents. However, it is convenient to put that consideration aside, and to begin (with Klein) at unidimensional measurement.
We are to measure, then, along a line. We will, for formal rhetoric's sake, conceive that line as returning into itself. We will, first, in order that we may apply numerical algebra, give a preliminary numbering to all the points of that line, so that every point has a number and but one number, and every real number, positive or negative, rational or surd, has a point and but one point, and so that the succession of any four numbers is the same as the succession on the line of the four corresponding points. Now, we must make a scale to shift along that line. We must imagine that we have a movable line which lies everywhere in coincidence with the fixed line, and which can be shifted. In the shifting, parts of it may become expanded or contracted, for we cannot tell whether they do or not unless we had some third standard to shift along to tell us; and then the same question would arise. But the continuity and succession of points shall not be broken in the shifting; and moreover, when the movable line has any one point brought back to coincidence with a former position, all the points shall be brought back. Now imagine all this extended to the imaginary numbers. Then, it is shown in the mathematical theory of functions, that if x be the number against which any point of the movable line falls in any one position and y be the number the same point falls against in any other position, it follows, because for each value of x there is just one value of y and for each value of y just one value of x, that x and y are connected by an equation linear in each, that is, an equation of the form
xy+Ax+By+C = 0.
This gives
y = -(Ax+C)/(x+B).
Now this is a function which forms the subject of some very beautiful and simple algebraical studies. †P1 It is convenient to put
A = B-α-β
C = B2-(α+β)B+αβ.
Then
| y | = ((α+β-B)x-B2+(α+β)B-αβ)/(x+B) |
| = (((α+β)x+(α+β)B-αβ)/(x+B))-B | |
| = (((α2-β2)(x+B)-αβ(α-β))/((x+B)(α-B)))-B | |
| = (((x+B-β)α2-(x+B-α)β2))/((x+B-β)α1-(x+B-α)β1)))-B |
But
x = ((x+B-β)α1-(x+B-α)β1)/((x+B-β)α°-(x+B-α)β°)-B.
So that the effect of the shifting has been to raise the exponents of α and β by 1.
It is easily proved that the same operation, performed any number t times, gives
((x+B-β)αt+1-(x+B-α)βt+1)/((x+B-β)αt-(x+B-α)βt)-B
If α has a modulus greater than that of β, it is easily seen that when t becomes a very large positive number, the first terms of numerator and denominator will become indefinitely greater than the second terms and the value will indefinitely approximate to
α-B.
But when t is a very large negative quantity, the reverse will occur, and the value will approximate toward
β-B.
143. If we look at the field of imaginary quantity, what we shall see is shown in the diagram.
Here we have a stereographic projection of the globe. At the south pole is β-B; at the north pole, α-B. The parallels are not at equal intervals of latitude but are crowded together infinitely about the pole. Now an increase of t by unity carries a point of the scale along a meridian from one parallel to the one next nearer the north pole. But an addition to t of an imaginary quantity carries the point of the scale round along a parallel.If the real line of the scale lies along a meridian all real shiftings of it will crowd its parts toward the north or the south pole; and the distance of either pole, as measured by the multitude of shiftings required to reach it, is infinite. †P1 The scale is limited, but immeasurable.
But if the real line of the scale lies along a parallel, real shiftings, that is shiftings from real points to real points, will carry it round, so that a finite number of shiftings will restore it to its first position. Such is the scale of rotatory displacement. It is unlimited, but finite, or measurable. A scale of measurement, in the sense here defined, cannot be both limited and finite. We seem to have such a scale in the measurement of probabilities. But it is not so. Absolute certainty, or probability 0 or probability 1 are unattainable; and therefore, the numbers attached to probabilities do not constitute any proper scale of measurement, which can be shifted along. But it is possible to construct a true scale for the measurement of belief. †P2 It was a part of the definition of a scale that in all its shiftings it should cover the whole of the line measured. ("For every point of the line a number of the scale in every position.") Hence the shifting can never be arrested by abuttal against a limit. If there is a limit, it must be at an immeasurable distance.
144. But there is a special case of measurement, very different from the one considered. Namely, it may happen that the nature of the shifting is such that [given] the equation
xy+Ax+By+C = 0,
where A, B, C, may have any values, real or imaginary, we have
C = 1/4(A+B)2.
Substituting this in the expressions for A and C in terms of α, β, and B, we get
1/4(α+β)2 = αβ
or
α = β.
This necessitates an altogether different treatment. In this case, we have
| y = | -((Ax+(1/4)(A+B)2)/(x+B)) |
| 2y = | -(A+B)+((B-A)(2x+A+B)/((B-A)+(2x+A+B))) |
| 2x = | -(A+B)+((B-A)(2x+A+B)/((B-A)+0(2x+A+B))) |
And t shifts give
-(A+B)+((B-A)(2x+A+B)/((B-A)+t(2x+A+B))).
This gives for t = ±∞, -(A+B). The scale is in this case then unlimited and immeasurable. This is the manner in which the Euclidean geometry virtually conceives lengths to be measured; but whether this method accords precisely with measurement by a rigid bar is a question to be decided experimentally, or irrationally, or not at all.
145. The fixed limits of measurement are very appropriately termed by mathematicians the Absolute. †P1 It is clear that even when measurement is not practical, even when we can hardly see how it ever can become so, the very idea of measuring a quantity, considerably illuminates our ideas about it. Naturally, the first question to be asked about a continuous quantity is whether the two points of its absolute coincide; if not, a second less important, but still significant question is whether they are in the real line of the scale or not. These are ultimately questions of fact which have to be decided by experimental indications; but the answers to them will have great bearing on philosophical and especially cosmogonical problems.
146. The mathematician does not by any means pretend that the above reasoning flawlessly establishes the absolute in every case. It is evident that it involves a premiss in regard to the imaginary points which only indirectly relates to anything in visible geometry, and which, of course, may be supposed not true. Nevertheless, the doctrine of the mathematical absolute holds with little doubt for all cases of measurement, because the assumptions virtually made will hardly ever fail.
147. When we pass to measurement in several dimensions, there seems to be little difference between one number of dimensions and another; and therefore we may as well limit ourselves to studying measurement on a plane, the only spatial spread for which our intuition is altogether effortless.
Radiating from each point of the plane is a continuity of lines. Each of these has upon it its two absolute points (possibly imaginary, and even possibly coincident); and assuming these to be continuous, they form a curve which, being cut in two points only by any one line, is of the second order. That is, it is a conic section, though it may be an imaginary or even degenerate one.
Now as the foot has different lengths in different countries, so the ratios of units of lengths along different lines in the plane is somewhat arbitrary. But the measurement is so made that first, every point infinitely distant from another along a straight line is also infinitely distant along any broken line; and second, if two straight lines intersect at a point, A, on the absolute conic and respectively cut it again at B and C; and from D, any point collinear with B and C, two straight lines be drawn, the segments of the first two lines, EF and GH, which these cut off, are equal. I omit the geometrical proof that this involves no inconsistency. This proposition enables us to compare any two lengths.
148. We now have to consider angular magnitude. In the space of experience, the evidence is strong that, when we turn around and different landscapes pass panorama-wise before our vision we come round to the same direction, and not merely to a new world much like the old one. In fact, I know of no other theory for which the evidence is so strong as it is for this. But it is quite conceivable that this should not be so; there might be a world in which we never could get turned round but should always be turning to new objects. But certain conveniences result from assuming for the measurement of the angles between lines the same absolute conic which is assumed as the absolute of linear measure. Thus, it is assumed that two straight lines meeting at infinity have no inclination to one another, just as it is assumed that in a direction such that the opposite infinities should coincide, all other points would have no distance from one another. The latter is another way of saying that if a point is at an infinite distance from another point on a straight line, it is so on a broken line. The other assertion is that if an infinite turning is requisite to reach a line from one centre, it is equally so if you attempt to reach it by turning successively about different centres. The analogue of the proposition for which the last figure was drawn is as follows:
Upon a line, a, tangent to the absolute let two points be taken from which the other tangents to the absolute are b and c. Through the intersection of b and c draw any line, d, then any two lines e and f, meeting at the intersection of a and b, make the same angle with one another as two other lines having the same intersections with d, and cutting one another at the intersection of a and c. This enables us to compare all angles.
149. Suppose a man to be standing upon an infinitely extended plane free from all obstructions. Would he see something like a horizon line, separating earth from sky, being the foreshortened parts of the plane at an infinite distance? If space is infinite, he would. Now suppose he sets up a plane of glass and traces upon it the projection of that horizon, from his eye as a centre. Would that projection be a straight line? Euclid virtually says, "Yes." Modern geometers say it is a question to be decided experimentally. As a logician, I say that no matter how near straight the line may seem, the presumption is that sufficiently accurate observation would show it was a conic section. We shall see the reason for this, when we come to study probable inference.
Let us suppose, then, that the horizon is not a straight line upon a level with the eye, but is a small circle below that level. If then two straight lines meet at infinity, their other ends must be infinitely distant; but the angle between them is null. Hence, there may be a triangle having all its angles null, and all its sides infinite. Let us assume (what might, however, be proved) that two triangles, having all the sides and angles of the one respectively and in their order equal to those of the other, are of equal area. Then all triangles having the sum of their angles null are of equal area. Call this T. Then the area of an ordinary polygon of V vertices all on the absolute is (V-2)T. The area of the absolute is therefore infinite.
If a triangle has two angles null and the third 1/N part of 180°, what is its area? Let ABD be the triangle, AB being on the absolute. Continue BD the absolute at C. Let ADE, EDF, etc., be N-1 triangles having their angles at D all equal to ADB. Then these N triangles are all equal, because their sides and angles are equal. They make a polygon of N+1 vertices on the absolute, the area of which is (N-1)T. Hence, the area of each triangle is (1-1/N)T.
What is the area of a triangle having one angle zero and the others mX180° and nX180°? Let AMN be such a triangle; extend MN on the side of N to the absolute at B. Then the area of ABM is (1-m)T and that of ABN is nT. Hence the area of AMN, which is their difference, is (1-m-n)T.
What is the area of a triangle having its three angles equal to lX180°, mX180°, and nX180°? Let LMN be such a triangle. Produce LM on the side of M to the absolute at A and join AN. Then if the angle MNA is put equal to x.180°, the area of ALN is (1-l-n-x)T, while that of AMN is (m-x)T. Hence, that of LMN, which is their difference, is (1-l-m-n)T.
Thus, the area of a triangle is proportional to the amount by which the sum of its angles falls short of two right angles. Of course, this does not forbid that amount being infinitely small for all triangles whose sides are finite.
150. The above reasoning may appear to be fallacious because it forgets that subtraction is not applicable to infinites. But it does not fall into that error. I may remark, however, that subtraction is applicable to infinites, in case their transformations are so limited that x+y cannot equal x+z unless y = z. For instance, we have considered the triangle ABC having two vertices on the absolute. This triangle is finite. But we might perfectly well reason about the infinite sector ABC provided this sector be not allowed to vary so as to change the area of the triangle, and provided, further, that we always add to each sector, BAC, its equal vertical sector B'AC'.
Looking at a triangle from this point of view, we see that the sum of the six sectors (two for each angle) is twice three times the triangle plus all the rest of the plane, or twice the area of the triangle plus the whole plane. The whole plane is four right angled sectors. But we have thus reckoned together with the sectors of the angles of the triangle their equal vertical sectors. Dividing by two, we find the sum of the angular sectors of a triangle is two right angles plus the area of the triangle.
Now since the sector is proportional to its angle, and since further, for the largest possible sector the angle is zero, it follows that the sector is equal to the negative of the angle, whence we find
area Δ = 2 ⥿ -Σ Angles.
151. . . . Such are the ideas which the mathematician is using every day. They are as logically unimpeachable as any in the world; but people, who are not sure of their logic, or who, like many men who pride themselves on their soundness of reason, are totally destitute of it, and who substitute for reasoning an associational rule of thumb, are naturally afraid of ideas that are unfamiliar, and which might lead them they know not whither.
As compared with imaginaries, with the absolute, and with other conceptions with which the mathematician works fearlessly — because good logicians, the Cauchys and the like, †P1 have led the way — as compared with these, the idea of an infinitesimal is exceedingly natural and facile. Yet men are afraid of infinitesimals, and resort to the cumbrous method of limits. This timidity is a psychological phenomenon which history explains. But I will not occupy space with that here. †1
It was Fermat, a wonderful logical and still more wonderful mathematical genius, whose light was almost extinguished by the bread-and-butter difficulties which the secret plotting of worldlings forced upon him, who first taught men the method of reasoning which lies at the bottom of all modern science and modern wealth, the method of the differential calculus. †2 He gave a variety of instructive examples, did this lawyer, this "conseiller de minimis," as the jealous Descartes was base enough to call him, joining himself to the "born missionaries" who were determined to "head off" this hope of mankind. But the first and simplest of them is the solution of the problem to divide a number, a, into two parts so that their product shall be a maximum. Let the parts be x and a-x. Let e be a quantity such that a+e is "adequal" or {parisos}, say perequal to a. Then, the product being a maximum is at the point when increase of x ceases to cause it to increase. Hence Fermat writes
x(a-x) = (x+e)(a-x-e)
which gives
0 = -xe+e(a-x-e)
or
0 = e(a-2x-e)
Fermat now divides both sides by e (which assumes e is not zero). Whence
0 = a-2x-e.
But a-2x-e is "adequal" to a-2x; and the e may consequently be "elided." Thus we get
0 = a-2x,
or
x = (1/2)a.
The peculiar properties of e, which we now call, after Leibniz, the infinitesimal, are:
First, that if pe = qe, then p = q, contrary to the property of zero; while
Second, that, under certain circumstances, we treat e as if zero, writing
p+e = p.
Of course, we cannot adopt the last equation without reservation. For it would follow that
e = 0,
whence, since
4×0 = 5×0,
4e = 5e,
and then by the first property,
4 = 5.
The method of indivisibles †P1 had recognized that infinitely large numbers may have definite ratios, so that division is applicable to them.
152. The simplest way of defending the algebraical device is to say that e represents a quantity immeasurably small, that is, so small that the Fermatian inference does not hold from these quantities to any that are assignable. That no contradiction is involved in this has been shown in the former part of this chapter. †1 In the sense of measurement, then, p+e = p, while from a formally logical point of view, it is assumed that e>0. This is the most natural way, a perfectly logical way, and the way the most consonant with modern mathematics.
It is also possible to conceive the reasoning to represent the following. (The problem is the same as above.) Let x be the unknown. Then, since x(a-x) is a maximum,
x(a-x)>(x+e)(a-x-e)
for all neighboring values of e. That is
0>e(a-2x-e).
Then the sign of a-2x-e is opposite to that of e no matter what the value of e. It follows that 2x differs from a by less than any assignable quantity.
The great body of modern mathematicians repudiate infinitesimals in the above literal sense, because it is not clear that such quantities are possible, or because they cannot entirely satisfy themselves with that mode of reasoning. They therefore adopt the method of limits, which is a method of establishing the fundamental principles of the differential calculus. I have nothing against it, except its timidity or inability to see the logic of the simpler way. Let x be a variable quantity which takes an unlimited series of values x1, x2, . . . xn, so that n will be a variable upon which xn, depends. If, then, there be a quantity c such that
x∞ = c,
that is, as the mathematicians prefer to say, in order to avoid speaking of infinity, if for every positive quantity e sufficiently small, there be a positive quantity ν such that for all values of n greater than ν
Modulus (xn-c)<e
then c is said to be the limit of x.
Upon this definition is raised quite an imposing theory about limits which I can only regard with admiration, when it is erected with modern accuracy. Only, I wish to point out that the need for such a definition is not limited to its application to n = ∞, nor because infinity presents peculiar difficulties. It is only because ∞ is not an assignable number with which we can perform arithmetical processes. Let the function xn = n2, then the same difficulty arises when n = Π, and the same definition of a limit is called for.
The differential calculus deals with continuity, and in some shape or other, it is necessary to define continuity. I accept the above definition, with unimportant modifications, as a good definition of continuity. From it, as it appears to me, the idea of infinitesimals follows as a consequence; but, if not, no matter — so long as the algebraic expression of the infinitesimal be accepted, which is really the essential point. Infinitesimals may exist and be highly important for philosophy, as I believe they are. But I quite admit that as far as the calculus goes, we only want them to reason with, and if they be admitted into our reasoning apparatus (which is the algebra) that is all we need care for.
Paper 5: A Theory about QuantityP †1
§1. The Cardinal Numerals
153. Quantity presents certain metaphysical difficulties, to appreciate which it would be as hopeless a task to bring this generation as to bring it to a sense of sin. Medieval doctors apprehended such points of logic far more clearly. Why a mass distant one yard from a pound of matter should gravitate toward that pound by precisely that fraction of an inch per second that it does, neither more nor less — how it is possible that the exact value of this quantity ever should be explained and brought under the manifest governance of that unyielding and universal law which is supposed to regulate all facts, how this can be when the general properties of an inch are nowise different from a mile, is a question which those philosophers who oppose my tychism †2 would find a puzzling one, could they once be brought to understand what this question is. My present purpose, however, is not to discuss this problem in its entirety, but merely to follow out, in a rambling spirit, a pretty little opening of thought suggested by an objection to a part of my solution of that problem.
154. That part of my solution is that Quantity is merely the mathematician's idealization of meaningless vocables invented for the experimental testing of orders of sequence. In our experience we often have occasion to remark that something is true of two or more things — say, for example, that one thing eats another, or that one day is pleasanter than another. A fact true of several subjects is called a "relation" between them. A fact true of a pair of subjects (as in the examples just suggested) is a "dyadic relation." Of some kinds of dyadic relation we find that if one thing, A, be so related to a second, B, while B is so related to a third thing, C, then A is always related in that same way to C. When this is so, the relation is said to be "transitive." We also call it a "succession" or "sequence." Now I hold that numbers are a mere series of vocables serving no other purpose than that of expressing such transitive relations, or, at least, no other purpose except one whose accomplishment is necessarily involved in that. I admit that our senses may inform us, not merely that A is heavier than B, but that A is a great deal more heavier than B, than C is heavier than D; and undoubtedly numbers do serve to express this verdict of sense with greater precision than sense can render it. But this, as I think, is a use of numbers which necessarily results from their primary use; the judgment, that one thing is much heavier than another, being a mere complexus of judgments each that one thing is heavier by a unit than another.
155. When a number is mentioned, I grant that the idea of a succession, or transitive relation, is conveyed to the mind; and insofar the number is not a meaningless vocable. But then, so is this same idea suggested by the children's gibberish
"Eeny, meeny, miney, mo,"
Yet all the world calls these meaningless words, and rightly so. Some persons would even deny to them the title of "words," thinking, perhaps, that every word properly means something. That, however, is going too far. For not only "this" and "that," but all proper names, including such words as "yard" and "metre" (which are strictly the names of individual prototype standards), and even "I" and "you," together with various other words, are equally devoid of what Stuart Mill †1 calls "connotation." Mr. Charles Leland informs us that "eeny, meeny," etc. are gipsy numerals. †2 They are certainly employed in counting nearly as the cardinal numbers are employed. The only essential difference is that the children count on to the end of the series of vocables round and round the ring of objects counted; while the process of counting a collection is brought to an end exclusively by the exhaustion of the collection, to which thereafter the last numeral word used is applied as an adjective. This adjective thus expresses nothing more than the relation of the collection to the series of vocables.
156. Still, there is a real fact of great importance about the collection itself which is at once deducible from that relation; namely, that the collection cannot be in a one-to-one correspondence with any collection to which is applicable an adjective derived from a subsequent vocable, but only to a part of it; nor can any collection to which is applicable an adjective derived from a preceding collection be in a one-to-one correspondence with this collection, but only with a part of it; while, on the other hand, this collection is in one-to-one correspondence with every collection to which the same numeral adjective is applicable. This, however, is not essentially implied as a part of the significance of the adjective. On the contrary, it is only shown by means of a theorem, called "The Fundamental Theorem of Arithmetic," †1 that this is an attribute of the collections themselves and not an accident of the particular way in which they have been counted. Nevertheless, this is a complete justification for the statement that quantity — in this case, multitude, or collectional quantity — is an attribute of the collections themselves. I do not think of denying this; nor do I mean that any kind of quantity is merely subjective. I am simply not using the word quantity in that acception. I am not speaking of physical, but of mathematical, quantity.
157. Were I to undertake to establish the correctness of my statement that the cardinal numerals are without meaning, I should unavoidably be led into a disquisition upon the nature of language quite astray from my present purpose. I will only hint at what my defence of the statement would be by saying that, according to my view, there are three categories of being; ideas of feelings, acts of reaction, and habits. †2 Habits are either habits about ideas of feelings or habits about acts of reaction. The ensemble of all habits about ideas of feeling constitutes one great habit which is a World; and the ensemble of all habits about acts of reaction constitutes a second great habit, which is another World. The former is the Inner World, the world of Plato's forms. The other is the Outer World, or universe of existence. The mind of man is adapted to the reality of being. Accordingly, there are two modes of association of ideas: inner association, based on the habits of the inner world, and outer association, based on the habits of the universe. †1 The former is commonly called association by resemblance; but in my opinion, it is not the resemblance which causes the association, but the association which constitutes the resemblance. An idea of a feeling is such as it is within itself, without any elements or relations. One shade of red does not in itself resemble another shade of red. Indeed, when we speak of a shade of red, it is already not the idea of the feeling of which we are speaking but of a cluster of such ideas. It is their clustering together in the Inner World that constitutes what we apprehend and name as their resemblance. Our minds, being considerably adapted to the inner world, the ideas of feelings attract one another in our minds, and, in the course of our experience of the inner world, develop general concepts. What we call sensible qualities are such clusters. Associations of our thoughts based on the habits of acts of reaction are called associations by contiguity, an expression with which I will not quarrel, since nothing can be contiguous but acts of reaction. For to be contiguous means to be near in space at one time; and nothing can crowd a place for itself but an act of reaction. The mind, by its instinctive adaptation to the Outer World, represents things as being in space, which is its intuitive representation of the clustering of reactions. What we call a Thing is a cluster or habit of reactions, or, to use a more familiar phrase, is a centre of forces. †2 In consequence, of this double mode of association of ideas, when man comes to form a language, he makes words of two classes, words which denominate things, which things he identifies by the clustering of their reactions, and such words are proper names, and words which signify, or mean, qualities, which are composite photographs of ideas of feelings, and such words are verbs or portions of verbs, such as are adjectives, common nouns, etc.
158. Thus, the cardinal numerals in being called meaningless are only assigned to one of the two main divisions of words. But within this great class the cardinal numerals possess the unique distinction of being mere instruments of experimentation. "This" and "that" are words designed to stimulate the person addressed to perform an act of observation; and many other words have that character; but these words afford no particular help in making the observation. At any rate, any such use is quite secondary. But the sole uses of the cardinal numbers are, first, to count with them, and second, to state the results of such counts.
159. Of course, it is impossible to count anything but clusters of acts, i.e., events and things (including persons); for nothing but reaction-acts are individual and discrete. To attempt, for example, to count all possible shades of red would be futile. True, we count the notes of the gamut; but they are not all possible pitches, but are merely those that are customarily used in music, that is, are but habits of action. But the system of numerals having been developed during the formative period of language, are taken up by the mathematician, who, generalizing upon them, creates for himself an ideal system after the following precepts.
§2. Precepts for the Construction of the System of Abstract NumbersP
160. First, There is a relation, G, such that to every number, i.e., to every object of the system, a different number is G and is G to that number alone; and we may say that a number to which another is G is "G'd" by that other;
Second, There is a number, called zero, 0, which is G to no cardinal number;
Third, The system contains no object that it is not necessitated to contain by the first two precepts. That is to say, a given description of number only exists provided the first two precepts require the existence of a number which may be of that description.
161. This system is a cluster of ideas of individual things; but it is not a cluster of real things. It thus belongs to the world of ideas, or Inner World. Nor does the mathematician, though he "creates the idea for himself," create it absolutely. Whatever it may contain of [that which is] impertinent [to Mathematics] is soilure from [elsewhere]. The idea in its purity is an eternal being of the Inner World.
162. This idea of discrete quantity having an absolute minimum subsequently suggests the ideas of other systems, all of which are characterized by the prominence of transitive relations. These mathematical ideas, being then applied in physics to such phenomena as present analogous relations, form the basis of systems of measurement. Throughout them all, succession is the prominent relation; and all measurement is affected by two operations. The first is the experiment of super-position, the result of which is that we say of two objects, A and B, A is (or is not) in the transitive relation, t, to B, and B is (or is not) in the relation, t, to A; while the second operation is the experiment of counting. The question "How much is A?" only calls for the statement, A has the understood transitive relation to such things, and such things have this relation to A.
§3. Application of the Theory to ArithmeticP
163. According to the theory partially stated above, pure arithmetic has nothing to do with the so-called Fundamental Theorem of Arithmetic. †1 For that theorem is that a finite collection counts up to the same number in whatever order the individuals of it are counted. But pure arithmetic considers only the numbers themselves and not the application of them to counting.
164. In order to illustrate the theory, I will show how the leading elementary propositions of pure arithmetic are deduced, and how it is subsequently applied to counting collections.
Corollary 1. No number is G of more than one number. For every number necessitated by the first precept is G to a single number, and the only number necessitated by the second precept, by itself, is G to no number. Hence, by the third precept, there is no number that is G to two numbers.
Corollary 2. No number is G'd by two numbers. For were there a number to which two numbers were G, one of the latter could be destroyed without any violation of the first two precepts, since the destruction would leave no number without a G which before had one, nor would it destroy 0, since that is not G. Hence, by the third precept, there is no number which is G to a number to which another number is G.
Corollary 3. No number is G to itself. For every number necessitated by the first precept is G to a different number, and to that alone; and the only number necessitated by the second precept, by itself, is G to no number.
Corollary 4. Every number except zero is G of a number. For every number necessitated by the first precept is so, and the only number directly necessitated by the second is zero.
Corollary 5. There is no class of numbers every one of which is G of a number of that class. For were there such a class, it could be entirely destroyed without conflict with precepts 1 and 2. For such destruction could only conflict with the first precept if it destroyed the number that was G to a number without destroying the latter. But no number of such a class could be G of any number out of the class by the first corollary. Nor could zero, the only number required to exist by the second precept alone, belong to this class, since zero is G to no number. Therefore, there would be no conflict with the first two precepts, and by the third precept such a class does not exist.
165. The truly fundamental theorem of pure arithmetic is not the proposition usually so called, but is the Fermatian principle, which is as follows:
Theorem I. The Fermatian Principle: Whatever character belongs to zero and also belongs to every number that is G of a number to which it belongs, belongs to all numbers.
Proof. For were there any numbers which did not possess that character, their destruction could not conflict with the first precept, since by hypothesis no number without that character is G to a number with it. Nor would their destruction conflict with the second precept directly, since by hypothesis zero is not one of the numbers which would be destroyed. Hence, by the third precept, there are no numbers without the character.
166. Definition 1. Any number, M, is, or is not, said to be greater than, a number, N, and N to be, or not to be, less than M, according to [whether] the following conditions are, or are not, fulfilled:
First, Every number G to another is greater than that other;
Second, Every number greater than a second, itself greater than a third, is greater than that third;
Third, No number is greater than another unless the above two conditions necessitate its being so.
Theorem II. Every cardinal number except zero is greater than zero. †1
Theorem III. No cardinal number L is greater than any number, M, unless L is G to a cardinal number, N, which either is greater than [or equal to] M.
Corollary 1. By the same reasoning (substituting everywhere less for "greater" and G'd by for "G of") no number M is less than any number L unless L be G to M or be greater than the number that is G to M.
Corollary 2. Hence, by the first and second conditions of the definition, if a cardinal number, L is greater than a cardinal number, M, then the number that is G to L is greater than the number that is G to M.
Corollary 3. Zero is greater than no number.
Corollary 4. Every number greater than a number is G of some number.
Theorem IV. No cardinal number is both greater and less than the same cardinal number.
Corollary 1. No number is either greater or less than itself.
Corollary 2. No cardinal number, M, is greater than a cardinal number, N, and less than GN.
Theorem V. Of any two different cardinal numbers, one is greater than the other.
Corollary. If the cardinal number, GL, that is G to L, be greater than the cardinal number, GM, that is G to M, by Theorem IV it cannot be less. Hence by Corollary 2 from Theorem III, L cannot be less than M. But by the first corollary from Theorem IV, GL is not GM, and therefore L is not M. Hence L is greater than M if GL is greater than GM.
167. Theorem VI. (Modified Fermatian Principle.) If a character, α, be such that, taking any two cardinal numbers, A and Z, either α does not belong to both A and Z, or no cardinal number is greater than A and less than Z, or SOME cardinal number greater than A and less than Z has the character, α, then, α is also such that, taking any two cardinal numbers, B and Y, either α does not belong both to B and Y, or no cardinal number is greater than B and less than Y, or EVERY cardinal number greater than B and less than Y has the character, α.
Proof. For were there an exception, there would be, at least, one cardinal number of a class we may call the n's fulfilling the conditions that every n is greater than B and less than Y and no number at once greater than an n and less than an n possess α. Then, by Corollary 4 of Theorem III, every n, and also every number greater than every n, would be G to some cardinal number; and by Corollary 5 from the general precepts there would be some n G to a cardinal number, not an n, which we may call M, and there would be some number greater than every n which would be G to some n which we may call N. But then GN and M would possess α, and if any n's existed, they would be greater than M and less than GN and yet there would be no cardinal number greater than M and less than GN having α. Hence it is absurd to suppose any exception.
168. Definition 2. A sum of a cardinal number, M, added to a cardinal number, N, is a cardinal number which fulfills the following conditions:
First, A sum of zero added to zero is zero;
Second, A sum of zero added to a cardinal number which is G to any cardinal number, N, is a number which is G to a sum of zero added to N;
Third, A sum of a cardinal number that is G to any cardinal number, M, added to any cardinal number, N, is a cardinal number which is G to a cardinal number which is a sum of M added to N;
Fourth, No cardinal number is a sum of a cardinal number added to a cardinal number unless it is necessitated to be so by the above conditions.
Theorem VII. There is one cardinal number, and but one, which is a sum of a cardinal number, M, added to a cardinal number, N.
Corollary 1. Whatever cardinal numbers M and N may be, M+N>0 unless M = N = 0.
Corollary 2. Whatever cardinal numbers M and N may be M+N>N unless M = 0, and M+N>M unless N = 0.
Corollary 3. Whatever cardinal numbers M and N may be, M+GN = G(M+N).
Corollary 4. Whatever cardinal number N may be, 0+N = N.
Corollary 5. Whatever cardinal number N may be, N+0 = N.
Corollary 6. Whatever cardinal numbers M and N may be, M+N = N+M.
Corollary 7. Whatever cardinal numbers L, M, and N may be, L+(M+N) = (L+M)+N.
Theorem VIII. The sum of a greater cardinal number, L, added to any cardinal number, N, is greater than the sum of a lesser cardinal number, M, added to the same cardinal number, N.
Corollary 1. Whatever cardinal numbers L, M, and N may be if L>M, then N+L>N+M.
Corollary 2. Whatever cardinal numbers A, B, C, D may be, if A>C and B>D then A+B>C+D.
Corollary 3. Whatever cardinal numbers L, M, and N may be unless L = M, L+N or N+L is not M+N or N+M.
Corollary 4. If L+N>M+N then L>M.
Corollary 5. If A+B>C+D, either A or B is greater than C and than D or else either C or D is less than A and than B.
Theorem IX. Whatever cardinal numbers L and M may be, there is one and only one cardinal number, N, such that either N+M = L or N+L = M.
Definition 3. The difference between two cardinal numbers, L and M, is such a number, N, that either N+M = L or N+L = M. It is said to be the remainder after subtracting the smaller as subtrahend, from the larger, as minuend. It is best denoted by the "minus sign" written after the larger of L and M and before the smaller.
Corollary 1. L-M is no cardinal number unless L>M.
Corollary 2. If L>M, then (L-M)+M = L.
Definition 4. The product of a cardinal number, M, multiplied into a cardinal number, N, or the product of the multiplicand, N, multiplied by the multiplier, M, is a cardinal number, written M×N, or M.N, or MN, subject to the following conditions:
First, zero is a product of any cardinal number multiplied by 0;
Second, a product of a cardinal number, N, multiplied by the cardinal number, GM, that is G to any cardinal number, M, is the sum, N+M.N, of N added to the product of M multiplied into N;
Third, no cardinal number is a product of cardinal numbers unless necessitated to be so by the foregoing conditions.
A product is said to be a multiple of its multiplicand.
Theorem X. There is one cardinal number and but one which is M.N a product of one cardinal number, M, multiplied into a given cardinal number, N.
Corollary 1. The product of any cardinal number, N, multiplied into zero is zero.
Corollary 2. Whatever cardinal numbers M and N may be M×N>0 unless M = 0 or N = 0.
Corollary 3. The product of any cardinal number, N, multiplied by the cardinal number that is G to zero (which is called 1, one) is N.
Corollary 4. The product of any cardinal number, N, multiplied into G0, or 1, is N.
Corollary 5. Whatever cardinal numbers M and N may be, M×GN = M+M.N.
Corollary 6. Whatever cardinal numbers M and N may be, M×N>M unless M = 0 or N = 0 or N = G0, and M×N>N unless N = 0 or M = 0 or M = G0.
Corollary 7. Whatever cardinal numbers L, M, and N may be, L.(M+N) = L.M+L.N.
Corollary 8. Whatever cardinal numbers L, M, N may be L.(M.N) = (L.M).N.
Corollary 9. Whatever cardinal numbers M and N may be M.N = N.M.
Theorem XI. Of two products of the same multiplicand not zero, that by the greater multiplier is the greater.
Corollary 1. If L>M, N.L>N.M unless N = 0.
Corollary 2. If A>C and B>D, A×B>C×D in all cases.
Corollary 3. Unless L = M, L×N is not M×N, unless N = 0.
Corollary 4. If L×N>M×N, then L>M in all cases.
Corollary 5. If A×B>C×D, either A or B is greater than C and than D, or C or D is less than A and than B.
Corollary 6. If either B or C is greater than A or than D, then B.C>A.D, unless A+D>B+C.
Definition 5. A divisor of a cardinal number, N, is a cardinal number which multiplied by a cardinal number gives N as product. The number, N, is said to be exactly divisible by its divisor.
Abbreviations. We may write N ≡ N' (mod M) where M is any cardinal number, not zero, to express that N and N' are cardinal numbers leaving the same remainder after division by M. We may denote the remainder and quotient of N divided by M by RmN and QmN, respectively. Then N = RmN+(QmN)·M.
We may denote GG0 by Q.
Scholium. The number Q is logically and mathematically peculiar. In old arithmetics multiplication and division by Q are considered as peculiar operations, Duplation and Mediation. We have need of an arithmetic of two, even in reasonings which do not concern quantity in the ordinary sense.
Theorem XII. Every cardinal number, N, has with reference to every cardinal number, M, except zero, a remainder, RmN, and a quotient, QmN; and only one number is remainder or quotient.
Corollary 1. If the cardinal number, N, is less than the modulus, M, its remainder, RmN = N.
Corollary 2. The remainder of the sum of two numbers, N and N', is the remainder of the sum of their remainders.
Corollary 3. The remainder of the product of two numbers, N and N', is the remainder of the product of the remainders.
Corollary 4. The quotient of the sum of two numbers is the sum of the quotient of the sum of the remainders added to the sum of the quotients of the numbers.
Corollary 5. The quotient of the product of two numbers, N and N', is the sum of the product of N by QmN', the quotient of the other, added to the quotient of the product of N by RmN', the remainder of the other. Or Qm(N.N') = N.QmN'+Qm(N.RmN').
Corollary 6. Given any cardinal number, N, and any modular number, M, there is a multiple of M greater than N. For (GQmN).M is such a multiple.
Definition 6. The powers of any cardinal number, B, called the base of the powers, are a class of cardinal numbers, each having a cardinal number, E, connected with it, called its exponent; and the power is written, BE, and powers and exponents are defined by the following conditions:
First, G0 is a power of B whose exponent is zero;
Second, The product of the power BE, of B with exponent E, multiplied by B is BGE, a power of B with exponent GE;
Third, No cardinal number is a power of a cardinal number, unless necessitated to be so by the foregoing conditions. Corollary. BG0 = B×B0 = B×G0 = B.
Theorem XIII. Given any two cardinal numbers, B and E, there is one, and but one cardinal number which is a power, BE, of B with exponent, E.
Corollary 1. Hence, 00 = G0 and is not indeterminate. In this respect, the definition here assumed differs from the usual one, which substitutes for the first condition B1 = B and adds the condition that BE = P if BGE = B.P. But practically the present definition is just as useful, if not more so, than the usual one.
Theorem XIV. A given exponent of two powers with the same exponent greater than zero, that with the greater base is the greater, and two powers of the same base greater than G0, that with the greater exponent is the greater.
Definition 7. An even number is a cardinal number whose remainder, relative to GG0 as modulus, is zero.
An odd number is a cardinal number whose remainder, relative to GG0 as modulus, is G0.
Corollary 1. Every cardinal number, N, is even or odd; and if N be even, GN is odd and vice versa.
Corollary 2. The double of a cardinal number, N, is N+N, the sum of N added to itself.
Corollary 3. If a number is even, it has a cardinal number that is half of it, but if it is odd, it has not.
Corollary 4. If the difference of two cardinal numbers, M and N, is even, those two numbers have a cardinal number as their arithmetical mean, and the difference between this mean and either M or N is half the difference between M and N.
169. Theorem XV. (Binary form of the Fermatian Principle.) If any character belongs to every power of GG0 and also to the mean of any two numbers having a mean, if it belongs to the numbers themselves, then it belongs to every cardinal number except 0.
Paper 6: Multitude and NumberP †1
§1. The Enumerable
170. Let us consider the relation of a constituent unit to the collective whole of which it forms a part. Suppose A to be such a unit and B to be such a whole. Then in order to avoid the circumlocution of saying that A is a constituent unit of B as the collective whole of which it is a unit, I shall simply say A is a unit of B, and shall write "A is a u of B"; or I may reverse the order in which A and B are mentioned by writing "B is u'd by A."
The only logical peculiarities of this relation are as follows:
First, Whatever is u of anything is u'd by itself and by nothing else. Hence, if anything is u'd by anything not itself, it is not itself u of anything; and consequently nothing that is u'd by anything but itself is u'd by itself.
Second, Whatever is not u'd by anything does not exist.
171. By a collection, I mean anything which is u'd by whatever has a certain quality, or general description, and by nothing else. That is, if C is a collection, there is some quality, α, such that taking anything whatever, say x, either x possesses the quality of α and is a unit of C, or else it neither possesses the quality α nor is a unit of C. On the other hand, if C is not a collection, no matter what quality or general description, β may be taken, there is either something possessing the quality β without being a unit of C, or there is some unit of C which does not possess the quality, β.
It will be perceived, therefore, that there is a collection corresponding to every common noun or general description. Corresponding to the common noun "man" there is a collection of men; and corresponding to the common noun "fairy" there is a collection of fairies. It is true that this last collection does not exist, or as we say, the total number of fairies is zero. But though it does not exist, that does not prevent it from being of the nature of a collection, any more than the non-existence of fairies deprives them of their distinguishing characteristics. . . .
172. Whether the constituent individuals or units of a collection have each of them a distinct identity of its own or not, depends upon the nature of the universe of discourse. If the universe of discourse is a matter of objective and completed experience, since experience is the aggregate of mental effect which the course of life has forced upon a man, by a brute bearing down of any will to resist it, each such act of brute force is destitute of anything reasonable (and therefore of the element of generality, or continuity, for continuity and generality are the same thing), and consequently the units will be individually distinct. It is such collections that I desire first to call your attention. I put aside then, for the present, such collections as the drops of water in the sea; and assume that the units are of such a kind that they may be absolutely distinguished from one another. Then, I say, as long as the discourse relates to a common objective and completed experience, those units retain each its distinct identity. If you and I talk of the great tragedians who have acted in New York within the last ten years, a definite list can be drawn up of them, and each of them has his or her proper name. But suppose we open the question of how far the general influences of the theatrical world at present favor the development of female stars rather than of male stars. In order to discuss that, we have to go beyond our completed experience, which may have been determined by accidental circumstances, and have to consider the possible or probable stars of the immediate future. We can no longer assign proper names to each. The individual actors to which our discourse now relates become largely merged into general varieties; and their separate identities are partially lost. Again, statisticians can tell us pretty accurately how many people in the city of New York will commit suicide in the year after next. None of these persons have at present any idea of doing such a thing, and it is very doubtful whether it can properly be said to be determinate now who they will be, although their number is approximately fixed. There is an approach to a want of distinct identity in the individuals of the collection of persons who are to commit suicide in the year 1899. When we say that of all possible throws of a pair of dice one thirty-sixth part will show sixes, the collection of possible throws which have not been made is a collection of which the individual units have no distinct identity. It is impossible so to designate a single one of those possible throws that have not been thrown that the designation shall be applicable to only one definite possible throw; and this impossibility does not spring from any incapacity of ours, but from the fact that in their own nature those throws are not individually distinct. The possible is necessarily general; and no amount of general specification can reduce a general class of possibilities to an individual case. It is only actuality, the force of existence, which bursts the fluidity of the general and produces a discrete unit. Since Kant it has been a very wide-spread idea that it is time and space which introduce continuity into nature. But this is an anacoluthon. Time and space are continuous because they embody conditions of possibility, and the possible is general, and continuity and generality are two names for the same absence of distinction of individuals.
When the universe of discourse relates to a common experience, but this experience is of something imaginary, as when we discuss the world of Shakespeare's creation in the play of Hamlet, we find individual distinction existing so far as the work of imagination has carried it, while beyond that point there is vagueness and generality. So, in the discussion of the consequences of a mathematical hypothesis, as long as we keep to what is distinctly posited and its positive implications, we find discrete elements, but when we pass to mere possibilities, the individuals merge together. This remark will be fully illustrated in the sequel.
173. A part of a collection called its whole is a collection such that whatever is u of the part is u of the whole, but something that is u of the whole is not u of the part.
174. It is convenient to use this locution; namely, instead of saying A is in the relation, r, to B, we may say A is an r to B, or of B; or, if we wish to reverse the order of mentioning A and B, we may say B is r'd by A.
If a relation, r, is such that nothing is r to two different things, and nothing is r'd by two different things, so that some things in the universe are perhaps r to nothing while all the rest are r, each to its own distinct correlate, and there are some things perhaps to which nothing is r, but all the rest have each a single thing that is r to it, then I call r a one-to-one relation. If there be a one-to-one relation, r, such that every unit of one collection is r to a unit of a second collection, while every unit of the second collection is r'd by a unit of the first collection, those two collections are commonly said to be in a one-to-one correspondence with one another. †1. . .
175. I shall use the word multitude to denote that character of a collection by virtue of which it is greater than some collections and less than others, provided the collection is discrete, that is, provided the constituent units of the collection are or may be distinct. But when the units lose their individual identity because the collection exceeds every positive existence of the universe, the word multitude ceases to be applicable. I will take the word multiplicity to mean the greatness of any collection discrete or continuous.
176. We have to note the precise meaning of saying that a relation of a given description exists. A relation of the kind here considered has been called an ens rationis; but it cannot be said that because nobody has ever constructed it — perhaps never will — it exists any the less on that account. Its existence consists in the fact that, if it were constructed, it would involve no contradiction. An easy dilemma will show that to suppose three things to be in one-to-one correspondence with individuals of a pair involves contradiction. But it is much more difficult to prove that a given hypothesis involves no contradiction. In mathematics, such propositions are usually replaced by so-called "problems." That is to say, a construction shows how the thing in question can take place. When we know how it can take place, we know, of course, that it is possible. Cases are rare in mathematics in which anything is shown to be possible without its being shown how. But when we come to philosophical questions, such a construction is generally practically beyond our powers; and it becomes necessary to examine the principles of logic in order to discover a general method of proving that a given hypothesis involves no contradiction. Without a thorough mastery of the principles of logic such a search must be fruitless.
Mathematics never has hypotheses forced upon it that are perplexing from [their] seemingly irresoluble mistiness — which is the aspect of such a question of philosophical possibility, at first sight. Mathematics does not need to take up any hypothesis that is not crystal-clear. Unfortunately, philosophy cannot choose its first principles at will, but has to accept them as they are.
177. For example, the relations of equality and excess of multitude having been defined after Cantor, philosophy can not avoid the question which instantly springs up: must every two collections be either equal or the one greater than the other, or can they be so multitudinous that the units of neither can be in one-to-one relation to units of the other?
To say that the collection of M's and the collection of N's are equal is to say:
There is a one-to-one relation, c, such that every M is c to an N; and there is a one-to-one relation, d, such that every N is d to an M.
To say that the collection of M's is less than the collection of N's is to say:
There is a one-to-one relation, c, such that every M is c to an N; but whatever one-to-one relation d may be, some N is not d to any M.
To say the collection of M's is greater than the collection of N's is to say:
Whatever one-to-one relation c may be, some M is not c to any N; but there is a one-to-one relation d such that every N is d to an M.
Now, formal logic suggests the fourth relation:
Whatever one-to-one relation c may be, some M is not c to any N, and whatever one-to-one relation d may be, some N is not d to any M.
Or this last may be stated more simply thus:
Whatever one-to-one relation c may be, some M is not c to any N and some N is not c'd by any M.
How shall we proceed in order to find out whether this last relation is a possible one, or not? . . .
178. In the first place, it must not be supposed that even if a collection is so great that the constituent units lose their individual identity, a one-to-one relation necessarily becomes impossible. If such a relation implied an actual operation performed, it would indeed be impossible, I suppose. But this is not the case. As the collection enlarges and the individual distinctions are little by little merged, it also passes out of the realm of brute force into the realm of ideas which is governed by rules. This sounds vague, because until I have shown you how to develop the idea of such a collection, I can offer you no example. But it is not necessary actually to construct the correspondence. It suffices to suppose that a certain number of units of the two collections having been brought into such a relation (and, in fact, they always are in such relations), then the general rules of the genesis of the two collections necessitate the falling of all the other individuals into their places in the correspondence. All this will become quite clear in the sequel.
179. That difficulty, then, having been removed, we have two collections, the M's and the N's; and the question is whether there is, no matter what these collections may be, always either some one-to-one relation, c, such that any M is c to an N or else some one-to-one relation, d, such that every N is d'd by an M. To begin with, there are vast multitudes of relations such that taking any one of them, r, every M is r to an N and every N is r'd by an M. For example, the relations of coexistence, maker of, non-husband of, etc. In general, each M can have any set of N's whatever as its correlates, except that there must be one of the M's that shall have among its correlates all those N's that are not r'd by any other M. And all those sets of N's for each M can be combined in any way whatever. In order to make our ideas more clear, let us for the moment suppose that the M's are equal to the finite number, μ, and the N's are equal to the finite number, ν. Then, for each M except one there are 2ν-1 different sets of N's, any one of which can be its correlates. Hence, there are (2ν-1)μ-1 different forms of the relation r, without taking account of the variety of different sets of correlates which the remaining M may have. Suppose we had a diagram of each of those relations, each diagram showing the collection of M's above and the collection of N's below, with lines drawn from each M to all the N's of which it was r. Each of that stupendous multitude of relations may be modified so as to reduce it [to] what we may call a one-to-x relation, by running through the N's and cutting away the connection of each N with every M but one; and each of the r relations could be thus cut down in a vast multitude of different ways. Call any such resulting relation, s. Then, every N would be s'd by a single M. Each one of the r relations could also be so modified as to reduce it to what we may call an x-to-one relation, by running through the M's and cutting off the connection of each M with every N but one. Call such a resulting relation, t. Then, every M would be t to a single N. Suppose we had a collection of diagrams showing all the ways in which every r relation could thus be reduced to an s relation or a t relation, that is, be reduced to a one-to-x relation or to an x-to-one relation. The question is, could the multitudes of M and N, be such that there would not be a single one-to-one relation among all those one-to-x relations [which each M has to an N] and x-to-one relations [which each N has to an M]? If among the diagrams of the one-to-x relations there were not one where the one-to-x relation was a one-to-one relation, it would be because in each case there was some M which was s [i.e., one-to-x] to two or more N's. If, then, there were any of these diagrams in which some M was not s to any N, those diagrams could be thrown out of consideration, because there was no necessity for a pluralism of lines to one M, as long as there were M's to which no line ran; and since there was no necessity for it, there is no need of modifying those diagrams so as to take away plural lines from some of the M's so as to give lines to all the M's, because, since there is a diagram for every possible modification changing an r [x-x] relation to an s [one-x] relation, there must already be a diagram remedying this fault. There must, therefore, be among the diagrams, some diagrams in which every M is s to an N — unless indeed there is a diagram where the s is a one-to-one relation. Taking, then, any diagram in which every M is s to an N, all it is necessary to do is to erase all the lines but one which go to each M, and the relation so resulting, which we may call u, is such that every M is u to an N, no N is u'd by two M's (for no N is s'd by two M's and the erasures cannot increase the relates of any N), and no M is u of two N's. In other words, u is a one-to-one relation, and every M is u of an N. Q.E.D.
Is this demonstration sound? It may be doubted; at any rate I can show you how by a very small modification it would certainly become unsound; and thus direct your attention to the point which requires scrutiny. If, instead of casting aside those diagrams of s relations which showed some M's that are not s to any N, I had proposed to cure them by changing the course of lines from M's having two or more lines to M's having none, until there were either no M's left without any lines or no M's left with pluralities of lines, I should have fallen into a gross petitio principii. For I should be assuming that, of those two classes of M's, the whole of one (whichever it might be) could be put into a one-to-one relation with the whole or a part of the other; and whether or not this is always possible is the very question at issue.
But the true argument is this: Nothing can force all of the s diagrams to show pluralities of lines to M's except the fact that some of them show lines to all the M's. For since all possibilities are represented in the diagrams, if all the diagrams show pluralities of lines to M's, there must be a logical necessity for this, so that the conditions would be contradicted if it were not so. Now the only logical necessity there can be in making some lines terminate at M's, that already have lines, is that there are no M's that have not already lines. Hence, in some cases, at least, all the M's must have lines.
The gist of this argument is that it considers in what way contradiction can arise, and thus shows that the only circumstance which could render the one-to-one correspondence impossible in one way, necessarily renders it possible in another way.
180. I will now prove two general theorems of great importance. The first is, that the collection of possible sets of units (including the set that includes no units at all) which can be taken from discrete collections is always greater than the collection of units. †1 . . .
The other theorem, which gives great importance to the first, is that if a collection is not too great to be discrete, that is, to have all its units individually distinct, neither is the collection of sets of units that can be generally formed from that collection too great to be discrete.
For we may suppose the units of the smaller collection to be independent characters, and the larger collection to consist of individuals possessing the different possible combinations of those characters. Then, any two units of the larger collection will be distinguished by the different combinations of characters they possess, and being so distinguished from one another they must be distinct individuals.
On those two theorems, I build the whole doctrine of collections.
181. I will now run over the different grades of multitude of discrete collections, and point out the most remarkable properties of those multitudes.
The lowest grade of multitude is that of a collection which does not exist, or the multitude of none. A collection of this multitude has obvious logical peculiarities. Namely, nothing asserted of it can be false. For of it alone contradictory assertions are true. It is a collection and it is not a collection. Given the premisses that all the X's are black and that all the X's are pure white, what is the conclusion? Simply that the multitude of the X's is zero.
The least difference by which one multitude can exceed another is by a single unit. But I do not say that the multitude next greater than a given multitude always exceeds it by a single unit.
The multitude of ways of distributing nothing into two abodes is one. This is the next grade of multitude. This again has certain logical peculiarities. Namely, in order to prove that every individual of it possesses one character, it suffices to prove that every individual of it does not possess the negative of that character.
The multitude of ways of distributing a single individual into two houses is two. This is the next grade of multitude. This again has certain logical peculiarities which have been noted in Schröder's Logik.
The multitude of combinations of two things is four, which is not the next grade of multitude. The multitude of combinations of four things is 16. The multitude of combinations of 16 things is 65,536. The multitude of combinations of 65,536 things is large. It is written by 20,036 followed by 19,725 other figures. The multitude of combinations of that many things is a number to write which would require over 600,000 thousand trimillibicentioctagentiseptillions of figures on the so-called English system of numeration. What the number itself would be called it would need a multimillionaire to say. But I suppose the word trimillillillion might mean a million to the trimillillionth power; and a trimillillion would be a million to the three thousandth power. But the multitude considered is far greater than a trimillillillion. It is safe to say that it far exceeds the number of chemical atoms in the gallactic cluster. Yet this is one of the early terms of a series which is confined entirely to finite collections and never reaches the really interesting division of multitudes, which comprises these that are infinite.
182. The finite collections, however, or, as I prefer to call them, the enumerable collections, have several interesting properties. The first thing to be considered is, how shall an enumerable multitude be defined? If we say that it is a multitude which can be reached by starting at 0, the lowest grade of multitude, and successively increasing it by one, we shall express the right idea. The difficulty is that this is not a clear and distinct statement. As long as we discuss the subject in ordinary language, the defect of distinctness is not felt. But it is one of the advantages of the algebra which is now used by all exact logicians, that such a statement cannot be expressed in that logical algebra until we have carefully thought out what it really means. An enumerable multitude is said to be one which can be constructed from zero by "successive" additions of unity. What does "successive," here, mean? Does it allow us to make innumerable additions of unity? If so, we certainly should get beyond the enumerable multitudes. But if we say that by "successive" additions we mean an enumerable multitude of additions, we fall into a circulus in definiendo. A little reflection will show that what we do mean is, that the enumerable multitudes are those multitudes which are necessarily reached, provided we start at zero, and provided that, any given multitude being reached, we go on to reach another multitude next greater than that. The only fault of this statement is, that it is logically inelegant. It sounds as if there were some special significance in the "reaching," which by the principles of logic there cannot be. For the enumerable multitudes are defined as those which are necessarily so reached. Now the kind of necessity to which this "necessarily" plainly refers is logical necessity. But the perfect logical necessity of a result never depends upon the material character of the predicate. If it is necessary for one predicate, it is equally so for any other. Accordingly, what is meant is that the enumerable multitudes are those multitudes every one of which possess any character whatsoever which is, in the first place, possessed by zero and, in the second place, if it is possessed by any multitude, M, whatsoever, is likewise possessed by the multitude next greater than M. We, thus, find that the definition of enumerable multitude is of this nature, that it asserts that that famous mode of reasoning which was invented by Fermat †1 applies to the succession of those multitudes. The enumerable multitudes are defined by a logical property of the whole collection of those multitudes.
183. Since the whole collection of enumerable multitudes has this logical property it follows a fortiori that every single enumerable multitude has the same property.
184. But it further follows from the same definition that every single enumerable collection has a further logical property.
This property is, that if an enumerable collection be counted, the counting process eventually comes to an end by the exhaustion of the collection. This property follows from the other, in this sense, that it is true of the zero collection, and if it be true of any collection whatever, it is equally true of every collection that is greater than that by one individual. Hence, it is true of all enumerable collections, by Fermatian reasoning.
185. You may ask why I should call this a logical property. It does not at first sight appear to be of that nature. But that is because it is not distinctly expressed. In place of "coming next after in the count," we may substitute any relation, r, such that not more than one individual (at least of the collection in question) is an r to any one. Then, the property is that if the M's form an enumerable collection, then and only then, if every M is r to an M [say, L], then every M is r'd by an M [say, N]. For example, in a count no M is immediately preceded by more than one M, hence it cannot be that every M immediately precedes an M (so that the collection is never exhausted) unless every M is immediately preceded by an M (in which case, the count would have no beginning). Because this is a logical necessity, the property is a logical property and is the foundation of that mode of inference for which De Morgan first gave the logical rules, under the name of the syllogism of transposed quantity. He, however, overlooked the fact that this mode of reasoning is only valid of enumerable collections. †1. . .
186. A remarkable and important property of enumerable collections is, that every finite part is less than a whole. If the finite part is measured, the multitude of units it contains is enumerable; and if it is incommensurable with the unit, the unit can be changed so as to make the finite part commensurable. Thus, to say that a finite part is less than its whole is the same as to say that an enumerable collection which is part of another is less than that other. There are two cases: first, when the whole is enumerable; and second, when the whole is inenumerable. Let us consider the first case. Let the M's be contained among the N's (which form an enumerable collection). Suppose however that the collection of M's is not less than that of the N's. Then, by the definition of equality, there is such a one-to-one relation d, that every N is d'd by an M. Then, since this M is an N, every N is d'd by an N. But d being a one-to-one relation, there are not two N's that are d'd by the same N. Hence, by the syllogism of transposed quantity, every N is d of an N. But the N's are, by their equality to the M's, d'd by nothing but M's. Hence, every N is an M. That is, we have shown that if the N's form an enumerable collection, the only collection at once contained in that collection and equal to that collection is the collection itself, and is not a part of the collection. That is, no part of an enumerable collection is equal to the collection. But the relation of inclusion is a one-to-one relation of every unit of the part to a unit of the whole. Hence, the part cannot be greater than the whole, and must be less than the whole.
We now take up the second case. But we can go further, and show that every inenumerable collection is greater than any enumerable collection. It is to be shown that it is absurd to suppose that every unit of an inenumerable collection, the N's, is in a one-to-one relation, c, to a unit of any one enumerable collection, the M's. Let r be such a one-to-one relation that every M except one is r to an M. Then, by the syllogism of transposed quantity, every M except just one is r'd by an M. (For if every M were r to an M, every M would be r'd by an M; and since r is a one-to-one [relation], if there is a single one of the connections or relations between pairs of individuals, which is excluded from r, it leaves just one M not r to an M and just one M not r'd by an M.) This is so whatever one-to-one relation r may be. Hence, were every N c to an M, it would follow that every N but one would be c to an M that was r to an M that was c'd by an N; and this compound relation of being 'c to an r of something c'd by' would be a one-to-one relation, being compounded of one-to-one relations. And invariably, whatever one-to-one relation r might be, one N would be the last in a count of the N's which should proceed from each N, say Ni, to that N, say Nj, such that Ni was c of that M that was r of that M which was c'd by Nj. In every such mode of counting, I say, some N would be the last N completing the count. And the M's being equal to the N's, and the one collection tied to the other by the relative, for every possible order of counting of the N's there would be some r relation among the M's; and thus in every possible counting of the N's there would be a last N, contrary to the hypothesis that the N's form an inenumerable collection. Thus, it is shown to be impossible that an inenumerable collection should be no greater than an enumerable collection, and the demonstration that a finite part is less than its whole is complete.
Now it is singular that every time Euclid reasons that a part is less than its whole, he falls into some fallacy, even though the part he is speaking of be finite. †P1 I can only account for it by supposing that owing to the falsity of his axiom, he learned to think that very wonderful things could be proved by its aid, things that he would know could never be proved by any other axiom; for when a man appeals to an axiom he is pretty sure to be reasoning fallaciously. And thus he was prevented from suspecting and thoroughly criticizing those places in his reasoning. . . .
187. It is a curious illustration of how even that part of mankind who reason for themselves more than any others — I mean the mathematicians — yet how even they follow phrases and forget their meanings, that while everybody is in the habit of calling the proposition that a part is less than its whole an axiom, yet when this proposition is stated in another form of words — for the transformation amounts to little more — we always speak of it as the fundamental theorem of arithmetic. The statement is that if in counting a collection with the cardinal numerals the count of a collection comes to a stop from the exhaustion of the individuals it always comes to a stop at the same numeral. I say that this amounts pretty much to saying that an enumerable part can not equal its whole. For to say that the same collection can in one order of counting count 16 and in another order of counting count 15 would be the same as to say that the first 16 numerals could (through the identity of the objects counted) be put into a one-to-one correspondence with the first 15 numerals; and this, by the definition of equality, would be to say that the collection of the first 15 numerals was equal to the collection of the first 16 numerals, although the former collection is an enumerable part of the latter.
It is generally understood to be very difficult to demonstrate this theorem logically, and so it is somewhat so if the principles of logic are not attended to. At any rate several of the proposed demonstrations egregiously beg the question. †P1
§2. The Denumerable
188. But I have lingered too long among enumerable multitudes. Let us go on to inquire what is the smallest possible multitude which is inenumerable?
Take the collection of M's. If this collection be such that taking any one-to-one relation r whatever, if every M is r to an M it necessarily follows that every M is r'd by an M, the collection of M's thereby fulfills the definition of an enumerable collection. We can substitute a phrase for the letter r in this statement and say that to call the collection of M's enumerable is the same as to assert that if every M, in any order of arrangement, is immediately succeeded by another M, and that an M which does not so immediately succeed any other of the M's, then every M immediately succeeds another M, and there is some ring arrangement without any first. To say that if there be no last there can be no first, is to say the collection spoken of is enumerable.
To deny that the M's are enumerable is, then, as much as to assert that there is a possible arrangement in which each M is immediately followed by another M which so follows no third M, and yet there is an absolutely first M which does not follow any M. If now we deny that the collection of M's is enumerable but, at the same time, restrict it to including no individual that need not be included to make the collection inenumerable, we shall plainly have a collection of the lowest order of multitude which any inenumerable collection can have. Such a collection I call denumerable. To say, then, that the collection of M's is denumerable, is the same as to assert that it contains nothing except one particular object and except what is implied in the fact that there is a one-to-one relation r such that every M is r to an M. This is a logical character; for it is the same as to say that the syllogism of transposed quantity does not hold good of it but that the Fermatian inference does. That is, if the collection of M's is denumerable, every character which is true of a certain M, say M0 and is also true of every M which is in a certain one-to-one relation to an M of which it is true, is necessarily true of every M of the collection.
For example, the entire collection of whole numbers forms a denumerable collection. For zero is a whole number, which is not greater by one than any number, there is a number greater by one than any given whole number, and there is no number or numbers which could be struck out of the collection and still leave it true that zero belonged to the collection and that there was a number of the collection greater by one than each number of the collection.
189. I have already shown by the example of the even numbers that a part of a denumerable collection may be equal to the whole collection. I will now prove that all denumerable collections are equal. For suppose that the M's and the N's are two denumerable collections. Then, a certain M can be found which we may call M0 such that taking a certain one-to-one relation, r, every M except M0 is r to an M, and there is an r to every M; and in like manner there is a one-to-one relation, s, such that every N except one, N0, is s to an N, and every N is s'd by an N. Then, I say, that the relation, c, can be so defined that every M is c to an N, and every N is c'd by an M. For let M0 be c to N0 and to nothing else; and let N0 be c'd by nothing but M0 and if anything, X, is c to anything, Y, let the r to X (and it alone) be c to the s of Y and to nothing else. Then, evidently c is a one-to-one relation. But every M is c to an N, because M0 is c to an N (namely to N0) and if any M is c to an N, then the r of that M is c to an N (for it is, by the definition of c, c to the s of the N to which the former M is c). And in like manner every N is c'd by an M, because N0 is c'd by an M (namely by M0), and if any N is c'd by an M, then the s of that N is c'd by an M (for it is, by the definition of c, c'd by the r of the M by which the former N is c'd). Q. E. D.
Accordingly, there is but a single grade of denumerable multitude. So it is to be noted as a defect in my nomenclature, which I unfortunately did not remark when I first published it, †1 that enumerable and denumerable, which sound so much alike, denote, the one a whole category of grades of multitude and the other a simple grade like, zero, or twenty-three.
190. It will be convenient to make here a few remarks about arithmetical operations upon multitude. Please observe that I have not said one word as yet about number, and I do not propose even to explain at all what numbers are until I have fully considered the subject of multitude, which is a radically different thing. Arithmetical operations can be performed upon both multitudes and upon numbers, just as they can be performed upon the terms of logic, the vectors of quaternions, the operations of the calculus of functions, and other subjects. What I ask you at this moment to consider is, not at all the addition and multiplication of numbers, for you do not know what I mean by numbers — it is safe to say so, since the word bears so many different meanings — but the addition and multiplication of multitudes.
Addition in general differs from aggregation inasmuch as a unit is increased by being added to itself but not by being aggregated to itself. When mutually exclusive terms are aggregated, that is the same as the addition of them. Addition might, therefore, be defined as the aggregation of the positings of terms. Two positings of the same term being different positings, their aggregate is different from a single positing of the term. The sum of two multitudes is the multitude of the aggregate of two mutually exclusive collections of those multitudes. The aggregate of a collection of collections of units may be defined as that collection of units, every unit of which is a unit of one of those collections, and which has every unit of any of those collections among its units.
191. It is easily proved that the sum of an enumerable collection of enumerable multitudes is an enumerable multitude. †2 . . .
192. The sum of an enumerable multitude and the denumerable multitude is denumerable. The proof is excessively simple; for we have only to count the enumerable collection in linear series, first. The count of that has to end; and then the denumerable series may follow in its primal order.
193. That the denumerable multitude added to itself gives itself is made plain by zigzagging through two denumerable series. But this comes more properly under the head of multiplication of multitudes, which I propose to consider.
Mathematicians seem to be satisfied so far to generalize the conception of multiplication as to make it the application of one operation to the result of another. But the conception may be still further generalized, and in being further generalized it returns more closely to its primitive type. The more general conception of multiplication to which I allude is expressed in the following definition: Multiplication is the pairing of every unit of one quantity with every unit of another quantity so as to make a new unit. Since there are two acceptions of the term pair — the ordered acception, according to which AB and BA are different pairs, and the unordered acception — there are two varieties of multiplication, the non-commutative and the commutative. Multiplication may further be distinguished into the free and the dominated. In free multiplication the idea of pairing remains in all its purity and generality. In dominated multiplication, the product of two units is that which results from the special mode of pairing which is of preëminent importance with reference to the particular kind of units that are paired. Thus, in reference to length and breadth the pairing of their units in units of area is preëminently important; in reference to an operator and its operant the pairing of their units in units of the result is preëminently important; in logic, in reference to two general terms, the pairing of their units in identical units which reunite their essential characters is preëminently important, etc. In the multiplication of multitudes we have one of the very rare instances of free multiplication. The product of a collection of multitudes called its factors may be defined as the multitude of possible sets of units any one of which could be formed out of units taken one from each of a collection of mutually exclusive collections of units having severally the multitudes of the factors. For example, to multiply 2 and 3, we take a collection of two objects, as A and B, and a distinct collection of three objects, as X, Y, and Z, and form the pairs AX, AY, AZ, BX, BY, BZ, which are all the sets that can be formed each from one unit of each collection. Then, since the multitude of these pairs is 6, the product of the multitudes, 2 and 3, is the multitude of 6.
194. The same general idea affords us a definition of involution. Involution is the formation of a new quantity a power from two quantities, a base, and an exponent, each unit of the power resulting from the attachment of all the units of the exponent each to some one unit of the base, without reference to how many units of the exponent are attached to any one unit of the base. Thus, 3 to the 2 power is the multitude of different ways in which both of two units, A and B, can be joined each to some one of three objects, X, Y, and Z. . . .
195. The product of two multitudes, μ and ν, is equal to the multitude of units in μ mutually exclusive collections each of ν units. For since there is one unit and but one for each of the ν units of each of the μ collections, these units are in one-to-one correspondence with the possible descriptions of single units each of which pairs a unit of a multitude of ν with a unit of a multitude of μ; and the multitude of such pairs is the product of μ and ν.
The μ power of ν is equal to the product of μ mutually exclusive collections each of ν units.
The product of two enumerable multitudes is an enumerable multitude.
The product of an enumerable multitude and the denumerable multitude is the denumerable multitude.
An enumerable power of the denumerable multitude is the denumerable multitude.
196. That the second power of the denumerable multitude is the denumerable multitude is easily seen by aggregating a denumerable series of collections, each a denumerable series of units.
Now we can start at the corner and proceeding from each unit we reach to a single next one and can reach any unit whatever in time without completing the proceeding. Hence, the whole forms one denumerable series. This proof is substantially that of Cantor. †1 The proposition being proved for two factors instantly extends itself to any enumerable multitude of factors. Of course, there is not the slightest difficulty in expressing this idea so as to construct the most rigidly formal demonstration. Let ℵ denote the denumerable multitude. Then, I am to show that ℵ2 = ℵ. Let the M's be a denumerable collection. That is, suppose
First: a certain object M0 is an M;
Second: there is a certain non-identical one-to-one relation, r, such that every M is r'd by an M;
Third: whatever is not necessitated to be an M by the above statements is not an M.
Let A and B constitute a collection of two objects not M's. Let us define the relation ς as follows:
First: the pair of attachments of A to M0 and B to M0 is ς'd by nothing;
Second: every pair of attachments of A to an M which we may call Mi other than M0 and of B to an M, which we may call Mj, is ς to the pair of attachments of A to that M which is r'd by Mi, and of B to that M which is r of Mj;
Third: every pair of attachments of A to M0 and of B to an M, which we may call Mk, is ς to the pair of attachments of A †1 to that M which is r of Mk, and of B †2 to M0;
Fourth: if one thing is not necessitated by the above rules to be ς to another, it is not ς to that other.
It is evident, then, that ς is a one-to-one relation; and it is evident that every pair of attachments of A to any M, say Mx, and of B to any M, say My, is ς of another such pair of attachments, that one such pair of attachments is ς'd by nothing, and that nothing is a pair of such attachments that is not necessitated to exist by the fact that everything is ς of something. Hence, the multitude of those pairs of attachments is denumerable; and that is the same as to say that the second power of the denumerable multitude is the denumerable multitude.
197. Dr. George Cantor †1 first substantially showed that between the units of any denumerable collection certain remarkable relations exist, which I call indefinitely divident relations. Namely, let the M's be any denumerable collection, and let f be any relation indefinitely divident of the collection of the M's. Then, no M is f to itself, but of any two different M's one is f to the other; and if an M is f to another it is f to every M that is f'd by that other; and if an M is f'd by another it is f'd by every M that is f to that other. And now comes the remarkable feature: If one M is f to another, it is f to an M that is not f'd by that other; whence, necessarily if one M is f'd by another, it is f'd by an M that is not f to that other.
There are vast multitudes of such indefinitely divident relations. I will instance a single one. If we take the whole series of vulgar fractions, those of the same denominator being taken immediately following one another in the increasing order of the numerators and those of different denominators in the increasing order of the denominators,
1/2 1/3 2/3 1/4 2/4 3/4 1/5 2/5 3/5 4/5 1/6 2/6 3/6 4/6 5/6 etc.
these evidently form a denumerable collection, for they form the aggregate of a denumerable collection of enumerable collections of units. If from this collection we omit those fractions which are equal to other fractions of lower denominations we plainly have still a denumerable collection. Now for the first of these denumerable collections, that of all the vulgar fractions, an indefinitely divident relation is that of being "greater than or equal to but of higher terms than". For the second of those denumerable collections, that of all the rational quantities greater than 0 and less than 1, an indefinitely divident relation is that of being "greater than." . . .
Numbers in themselves cannot possibly signify any magnitude other than the magnitudes of collections, or multitude; but what they principally represent is place in a serial order. Numbers do not contain the idea of the equality of parts and consequently a fraction cannot in itself signify anything involving equality of parts. They merely express the ordinal place in such a uniformly condensed series. . . . †1
198. A striking difference between enumerable and denumerable collections is this, that no arrangement of an enumerable collection has any different properties from any other arrangement; for the units are or may be in all respects precisely alike, that is, have the same general characters, although they differ individually, each having its proper designation. But it is not so with regard to denumerable collections. Every such collection has a primal arrangement, according to its generating relation. There is one unit, at least, which arbitrarily belongs to the collection just as every unit of an enumerable collection belongs to that collection. But after that one unit, or some enumerable collection of units, has been arbitrarily posited as belonging to the collection, the rest belong to it by virtue of the general rule that there is in the primal arrangement one unit of the collection next after each unit of the collection. Those last units cannot be all individually designated, although any one of them may be individually designated. Nor is this merely owing to an incapacity on our part. On the contrary, it is logically impossible that they should be so designated. For were they so designated there would be no contradiction in supposing a list of them all to be made. That list would be complete, for that is the meaning of all. There would therefore be a last name on the list. But that is directly contrary to the definition of the denumerable multitude.
The same truth may be stated thus: It is impossible that all the units of a denumerable collection should have the same general properties. For the existence of the primal arrangement is essential to it, being involved in the very definition of the denumerable collection as that of smallest multitude greater than every enumerable collection. Now, this primal arrangement is an arrangement according to a general rule, and its statement constitutes, therefore, general differences between the units of the denumerable collection.
On the other hand any unit whatever of a denumerable collection may be individually designated, as well as all those which precede it in the primal arrangement. And these can be all exactly alike in their general qualities. Yet there must always be a latter part of the collection which is not individually designated but is only generally described. In this part we recognize an element of ideal being as opposed to the brute and surd existence of the individual.
The denumerable collection of whole numbers, for example, constitutes a discrete series, in the sense that there is not one which may not be distinguished completely and individually from its neighbors.
But we cannot with any clearness of thought carry these reflections further until we are in possession of an instance of a greater collection.
199. The arrangement of a denumerable collection according to an indefinitely divident relation like the rational numbers — or to take a simpler instance, like the fractions which can be written in the binary system of arithmetical notation with enumerable series of figures — is a very recondite arrangement, not at all naturally suggested by the primal arrangement. This is shown by the fact that the world had to wait for George Cantor to inform it that the collection of rational fractions was a collection precisely like that of the whole numbers. †1
This remark will be found important in the sequel.
§3. The Primipostnumeral
200. So much, for the present, for the denumerable multitude. Let us now inquire, what is the smallest multitude which exceeds the denumerable multitude? An enumerable or denumerable multitude is a multitude such that whatever in any arrangement of an enumerable collection, in the primal arrangement of a denumerable collection, is true of the first unit, and is further true of any unit which comes next after any unit of which it is true, is true of all and every unit of the collection. . . . It has not yet been proved that there is any such minimum multitude among those which exceed the denumerable; but it is convenient to say that in fact there is. I have hitherto named this multitude, which was first clearly described by Cantor, †1 the first abnumeral multitude. †2 But I find that a name in one word is wanted. So I will hereafter name it the primipostnumeral multitude.
201. Suppose it to be true of a collection that in whatever way its units be arranged in a horizontal line with one unit to the extreme left, and a unit next to the right of each unit, there is something which is true of the first unit and which if true of any unit is always true of the next unit to the right, which nevertheless is not true of all the units; and suppose furthermore that the collection is no greater than it need be to bring about that state of things. Then, that collection is by definition a primipostnumeral collection. Or by the aid of the logic of relatives, we may state the matter as follows:
1. Let there be an existent collection, R;
2. Let R include no unit which is not necessitated by that condition;
3. Let r be a one-to-one relation between units;
4. Let there be a collection, the Q's, such that no Q is R;
5. Let there be a Q that is r to each unit of the collections of the Q's and R's;
6. Let the collection of the Q's include nothing not necessitated by the foregoing conditions;
7. Let h be a one-to-one relation of a unit to a collection;
8. Let there be a collection, P, such that no P is a Q or R;
9. Let there be a P which is h to every (denumerable) collection of Q's.
10. Let there be no P which is not necessitated in order to fulfill the foregoing conditions.
Then, the collection of P's is a primipostnumeral collection.
It would be easy to make this statement more symmetrical in appearance; but I prefer to make it perspicuous. Thus, we might make r a relation between a unit and an enumerable collection; and we might make the P's include an h for every denumerable collection of P's, Q's and R's, etc. The word "denumerable" in the ninth condition is added merely for the sake of perspicuity.
The second, sixth, and tenth conditions are not very clear. The meaning is that the multitude is no larger than need be.
202. The definitions of a primipostnumeral collection just given suppose it to be constructed from a denumerable collection. But if we attempt to form a primipostnumeral collection from a denumerable collection in its primal arrangement we shall fail ignominiously.
Let us, for example, imagine a series of dots representing, the first [dot] the position of the tortoise when Achilles began to run after him, and each successive dot the position of the tortoise at the instant when Achilles reached the position represented by the preceding dot. If there are no more dots than are necessary to fulfill this condition, the collection of dots is denumerable. If we add a dot to represent the position of the tortoise at the moment when Achilles catches up with him, the Fermatian inference seems at first sight not to hold good. For the first dot represents a position of the tortoise before Achilles had caught up with him, and if any dot represents the position of the tortoise before Achilles caught up with him, so likewise does the dot which immediately succeeds it. The Fermatian inference then would seem to be that every dot represents a position of the tortoise before Achilles had caught up with him. Yet this is not true of the last dot which represents the position of the tortoise at the moment when Achilles caught up with him. Yet but one dot has been added to the denumerable collection, and of course, it remains denumerable. The only reason that the inference does not hold is that the dots are no longer in their primal arrangement. Put the last dot at the beginning, so as to preserve the primal arrangement, and any Fermatian inference whose premisses were true would hold good. The point I wish to make is that the denumerable collection in its primal order leads to no way of constructing or of conceiving of a primipostnumeral collection. Of course, we can say, "Let there be a dot for each denumerable collection of the tortoise-places;" but we might as well omit the tortoise-places and say, "Let there be a primipostnumeral collection of dots." The primal arrangement of the denumerable collection affords no definite places nor approximations to the places for the primipostnumeral collection.
203. The reason is that the latter part of the denumerable collection, which is its denumerable point, is all concentrated towards one point, whether that point be a metrically ordinary point or a point at infinity. This fault is remedied in the indefinitely divident arrangement. Here the denumerable part of the collection is spread over a line.
In this case, if we imagine all those subdivisions to be performed which are implied by saying that the intervals resulting from each set of subdivisions are all subdivided in the next following set of subdivisions, the multitude of subdivisions is 2ℵ where ℵ is the denumerable multitude; and this is no mere algebraical form without meaning. It has a perfectly exact meaning which I explained in speaking of the effects of addition, multiplication, and involution upon multitudes.
Moreover, you will remember that I distinctly and fully proved †1 that the multitude of possible sets of units each of which can be formed from the units of a collection always exceeds the multitude of that collection, provided it be a discrete collection.
204. Do you not think it possible that the stellar universe extends throughout space? If so, the whole collection of worlds is at least denumerable. At any rate, it is perfectly possible that the whole collection of intelligent beings who live, have lived, or will live anywhere is at least equal to the collection of whole numbers. It is conceivable that they are all immortal and that each one should be given each hour throughout eternity the name of one of them and he should assign that person in wish to heaven or to hell, so that in the course of eternity he would wish every one of them to heaven or to hell. Could they by all making different wishes wish among them for every possible distribution of themselves to heaven or to hell? If not, the multitude of such possible distributions is greater than the denumerable multitude. But they plainly could not wish for all possible such distributions. For if they did, some one would necessarily be perfectly satisfied with every possible distribution. But one possible distribution would consist in sending each person to the place he did not wish himself to go; and that would satisfy nobody. It was Cantor who first proved that the surd quantities form a collection exceeding the collection of rational quantities. †2 But his method was only applicable to that particular case. My method is applicable to any discrete multitude whatever and shows that 2μ>μ in every case in which μ is a discrete multitude.
205. I will give a few more examples of primipostnumeral collections. The collection of quantities between zero and unity, to the exact discrimination of which decimals can indefinitely approximate but never attain, is evidently 10ℵ, which of course equals 2ℵ. For 16ℵ = (24)ℵ = 2(4ℵ) = 2ℵ.
The collection of all possible limits of convergent series. whose successive approximations are vulgar fractions, although it does not, according to any obvious rule of one-to-one correspondence, give a limit for every possible denumerable collection of vulgar fractions, does nevertheless in an obvious way correspond each limit to a denumerable collection of vulgar fractions, and to so large a part of the whole that it is primipostnumeral, as Cantor has strictly proved. †1
206. Just as there is a primal arrangement of every denumerable collection, according to a generating relation, so there is a primal arrangement of every primipostnumeral collection, according to a generating arrangement. This primal arrangement of the primipostnumeral collection springs from a highly recondite arrangement of the denumerable collection. Namely, we must arrange the denumerable collection in an indefinitely divident order, and then the units, which are implied in saying that the denumerable succession of subdivisions have been completed constitute the primipostnumeral collection. But when I say that the primipostnumeral collection springs from an arrangement of the denumerable collection, I do not mean that it is formed from the denumerable collection itself; for that would not be true. On the contrary, the primipostnumeral collection can only be constructed by a method which skips the denumerable collection altogether. In order to show what I mean I will state the definition of a primipostnumeral collection in terms of relations. There are two or three trifling explanations to be made here. First an aggregate of collections is a collection of the units of those collections. It is also an aggregate of the collections, which are called its aggregants. Just as to say that Alexander cuts some knot implies that a knot exists, although to say Alexander cuts every knot, i.e., whatever knot there may be, does not imply the existence of any knot, the latter by its generality referring to an ideal being, not to a brute individual existence, so to say that a collection has a certain collection as its aggregant implies the existence of the latter collection and therefore that it contains at least one unit. I must also explain that whenever I say either one thing or another is true I never thereby mean to exclude both.
207. I will now describe a certain collection A, whose units I will call the P's [Π's?].
First, The Π's can be arranged in linear order. That is, there is a relation, p, such that taking as you will any Π's, individually designable as Π1, Π2, and Π3, either Π3 is not p to Π2 or Π2 is not p to Π1 or (if Π3 is p to Π2 and Π2 is p to Π1), Π3 is p to Π1;
Second, The line of arrangement of the Π's can be taken so as not to branch. That is, taking as you will Π's, individually designable as Π4 and Π5, either Π4 is p to Π5 or Π5 is p to Π4; (of course this permits both to be true, but that I proceed to forbid).
Third, The line of arrangement of the Π's can further be so taken as not to return into itself, circularly. That is, taking as you will any Π, individually designable as Π6, Π6 is not p to Π6;
Fourth, There are certain parts of A called "packs" of Π, which are mutually exclusive. That is, taking any pack whatever and any unit of that pack, that unit is a Π; and taking as you will any packs individually designable as P7 †1 and P8, and any Π's individually designable as Π7 and Π8, either P7 is identical with P8 or Π7 is not a unit of P7, or Π8 is not a unit of P8, or else Π7 is not identical with Π8;
Fifth, The packs can be arranged in linear order. That is, there is a relation, s, such that taking as you will any P's, individually designable as P1, P2, and P3, either P3 is not s to P2, or P2 is not s to P1, or P3 is s to P1;
Sixth, The line of arrangement of the packs can be taken so as not to branch. That is, taking as you will any P's, individually designable as P4 and P5, either P4 is s to P5 or P5 is s to P4;
Seventh, The line of arrangement of the packs can be further taken so as not to return into itself. That is, taking as you will any pack individually designable as P6, P6 is not s to P6;
Eighth, The arrangement of the packs can further be such that each pack is immediately succeeded by a next following pack. That is, taking as you will any pack individually designable as P9, a pack individually designable as P10 can be found such that P10 is s to P9; and such that taking thereafter as you will any pack individually designable as P11, either P11 is not p to P9, or P11 is not p'd by P10;
Ninth, Such a succession of packs is not a mere idea, but actually exists if the collection A exists. That is, a certain collection, P0, is such a pack;
Tenth, Each pack contains a unit which, in the linear order of the Π's, comes next after each unit of any of those packs which precede this pack in the linear order of the packs. That is, taking as you will any packs, individually designable as P12 and P13, and any unit, individually designable as Π12, a unit, individually designable as Π13, can be thereafter found such that, taking as you will any pack individually designable as P14 and any unit individually designable as Π14, either P13 is not s to P12, or Π12 is not a unit of P12, or Π13 is p to Π12; and either P13 is not s to P14 or Π14 is not a unit of P14, or Π12 is p to Π14, or Π13 is not p to Π14;
Eleventh, No varieties of descriptions of Π's exist than those which are necessitated by the foregoing conditions;
Twelfth, No varieties of descriptions of packs exist than those which are necessitated by the foregoing conditions.
This collection of Π's is primipostnumeral; and you will see what I mean by saying that the construction skips the denumerable multitude, if you consider how many Π's are contained in each pack. The pack P0 is obliged by the ninth condition to exist, so that it must contain at least one Π. But nothing obliges it to contain a Π which is other than any Π which it contains; and therefore the twelfth condition forbids it to contain [more than] one Π. It consists, therefore, of a single Π. If we arrange the Π's in a horizontal row so that p shall be equivalent to being "further to the right than," then that P which is s to P0, but is not s to any other pack, which pack we may call P1, must contain one Π to the right of the Π of [P0]. It need contain no other, and therefore cannot contain any other.
P2 contains a Π immediately to the right of that of the P0 and another to the right of that of P1, and after this each pack contains double the units of the preceding. Thus, Pn+1 contains 2n units. As long as n is enumerable, this is enumerable. But as soon as n becomes denumerable, it skips the denumerable multitude and becomes primipostnumeral.
208. In order to prove that any proposition is generally true of every member of a denumerable collection, it is always necessary — unless it be some proposition not peculiar to such a collection — to consider the collection either in its primal arrangement, or in reference to some relation by which the collection is generable, and then reason as follows, where r is the generating relation, and M0 is that M which is not r to any M:
M0 is X,
If any M is X then the r of M is X;
∴Every M is X.
Without this Fermatian syllogism no progress would ever have been made in the mathematical doctrine of whole numbers; and though by the exercise of ingenuity we may seem to dispense with this syllogism in some cases, yet either it lurks beneath the method used, or else by a generalization the proposition is reduced to a case of a proposition not confined to the denumerable multitude.
209. In like manner, in order to prove that anything is true of a primipostnumeral collection, unless it is more generally true, we must consider that collection in its primal arrangement or with reference to a relation equivalent to that of its primal arrangement. The special mode of reasoning will be as follows:
Π0, the unit of P0, is X,
If every Π of any pack is X, then every Π of the pack which is s of that pack is X;
Hence, every Π is X.
This may be called the primipostnumeral syllogism.
210. Every mathematician knows that the doctrine of real quantities is in an exceedingly backward condition. It cannot be doubted by any exact logician that the reason of this is the neglect of the primipostnumeral syllogism without which it is as impossible to develop the doctrine of real quantities, as it would be to develop the theory of numbers without Fermatian reasoning.
I do not mean to say that the primipostnumeral syllogism is altogether unknown in mathematics; for the reasoning of Ricardo †1 in his theory of rent, reasoning which is of fundamental importance in political economy, as well as much of the elementary reasoning of the differential calculus, is of that nature. But these are only exceptions which prove the rule; for they strongly illustrate the weakness of grasp, the want of freedom and dexterity with which the mathematicians handle this tool which they seem to find so awkward that they can only employ it in a few of its manifold applications.
211. In the denumerable multitude we noticed the first beginnings of the phenomenon of the fusion of the units. All the units of the first part of the primal order of a denumerable multitude can be individually designated as far as we please, but those in the latter part cannot. In the primipostnumeral multitude the same phenomenon is much more marked. It is impossible to designate individually all the units in any part of a primipostnumeral multitude. Any one unit may be completely separated from all the others without the slightest disturbance of the arrangement.
Thus, we may imagine points measured off from 0 as origin
toward A to represent the real quantities from zero toward √2. Let A be the point which according to this measurement would represent √2. But we may modify the rule of one-to-one correspondence between quantities and points, so that, for all values less than √2, the points to the left of A represent those values, while another point an inch or two to the right shall represent √2, and all quantities greater than √2 shall be represented by points as many inches or parts of an inch to the right of a third point, C, several inches to the right of B, as there are units and parts of units in the excess of those quantities over √2. This mode of representation is just as perfect as the usual unbroken correspondence. It represents all the relations of the quantities with absolute fidelity and does not disturb their arrangement in the least.
It is, therefore, perfectly possible to set off any one unit of a primipostnumeral collection by itself, and equally possible so to set off any enumerable multitude of such units. Nor are there any singular units of the collection which resist such separation.
I will give another illustration. It is perfectly easy to exactly describe many surd quantities simply by stating what their expressions in the Arabic system of notation would be. This may sound very false; but it is so, nevertheless. For instance, that quantity, which is expressed by a decimal point followed by a denumerable series of figures, of which every one which stands in a place appropriated to (1/10)n where n is prime shall be a figure 1, while every one which stands in a place whose logarithm n is composite shall be a cipher, is, we know, an irrational quantity. Now, I do not think there can be much doubt that, however recondite and complicated the descriptions may be, every surd quantity is capable in some such way of having its expression in decimals exactly described.
Thus every unit of a primipostnumeral collection admits of being individually designated and exactly described in such terms as to distinguish it from every other unit of the collection. Thus, notwithstanding a certain incipient cohesiveness between its units, it is a discrete collection, still. . . .
212. It is one of the effects of the deplorable neglect by mathematicians of the properties of primipostnumeral collections that we are in complete ignorance of an arrangement of such a collection, which should be related to its primal arrangement in any manner analogous to the relation of the arrangement [of] the primal arrangement of the denumerable collection to that indefinitely divident arrangement, which leads to a clear conception of the next grade of multitude.
I have had but little time to consider this problem; but I can produce an arrangement which will be of some service. Suppose that instead of proceeding, as in the usual generation of the primipostnumeral multitude, to go through a denumerable series of operations each consisting in interpolating a unit between every pair of successive units, we go through a denumerable multitude of operations each consisting in replacing every pair by an image of the whole collection. For example, using the binary system of arithmetical notation, suppose we begin with a collection of two objects, zero and one-half.
| .0 | .1 |
Each operation may consist of replacing each number by a sub-collection of [all the] numbers, each consisting of two parts, the first part being the figures of the number replaced, the second [being the figures of one of] the numbers composing the whole collection. Thus, the result of the first operation will be
| .00 | .01 | .10 | .11 |
The result of the second operation will be
| .0000 | .0001 | .0010 | .0011 | .0100 | .0101 | .0110 |
| .0111 | .1000 | .1001 | .1010 | .1011 | .1100 | .1101 |
| .1110 | .1111 |
The next result would be 256 numbers, the next 65,536 numbers, the next 4,294,867,296. The result of a denumerable succession of such operations will evidently be to give all the real quantities between zero and one, which is a primipostnumeral collection.
§4. The Secundopostnumeral and Larger Collections
213. Although I have not touched upon half the questions of interest concerning the primipostnumeral multitude, I must hurry on to inquire, what is the least multitude greater than the primipostnumeral multitude? Time forbids my going through a fundamentally methodical discussion of this problem. But the speediest route to a correct solution of a difficult logical crux lies almost always through that paradox or sophism which depends upon that crux. Let us recur then for a moment to the indefinitely divident arrangement of a primipostnumeral collection. It will be convenient to use the binary system of arithmetical notation. We begin with .0 as our Π0. P1 consists
of a fraction equal to that but carried into the first place of secundals and of corresponding units which differ only in having a 1 in the first place of secundals. P2 consists of fractions equal to those but carried into the second place of secundals, together with fractions differing from them only in having a 1 in the second place of secundals. And so on. Now if we use all the enumerable places of secundals, but stop before we reach any denumerable place, we shall have, among all the packs, all the fractions whose denominators are powers of 2 with enumerable exponents, and therefore we shall plainly have only a denumerable collection. But if n is the number of packs up to a given pack, then the number of fractions will be 2n-1. When we have used all the enumerable places of secundals and no others, how many packs have we used? Plainly a denumerable collection, since the multitude of enumerable whole numbers is denumerable. It would appear, then, that 2n-1, when n is denumerable, is denumerable. But on the contrary, if we consider only that pack which fills every enumerable place of secundals, since it contains the expression in secundals of every real quantity between 0 and 1, it alone is a primipostnumeral collection. Moreover, the number of Π's in Pn is 2n and since n is denumerable for this collection, it follows that 2n is primipostnumeral. And it is impossible that the subtraction of one unit should reduce a primipostnumeral collection to a denumerable collection. Again, every pack contains a multitude of individuals only 1 more than that of all the packs that precede it in the order of the packs. How then can the former be primipostnumeral while the latter is denumerable?
The explanation of this sophism is that it confounds two categories of characters of collections, their multitudes and their arithms. The arithm of a multitude is the multitude of multitudes less than that multitude. Thus, the arithm of 2 is 2; for the multitudes less than 2 are 0 and 1. By number in one of its senses, that in which I endeavor to restrict it in exact discussions, is meant an enumerable arithm. Thus, the arithm or number of any enumerable multitude is that multitude. The arithm of the denumerable multitude, also, is that multitude. But the arithm of the primipostnumeral multitude is the denumerable multitude. The maximum multitude of an increasing endless series that converges to a limit is the arithm of that limit, in this sense, that by the limit of an increasing endless series is meant the smallest multitude greater than all the terms of the series. If there is no such smallest multitude the series is not convergent. If, then, by the maximum multitude of an increasing series we mean the multitude of all the multitudes which would converge increasingly to the given limit, this maximum multitude is plainly the arithm of the series. Thus, the series of whole numbers is an increasing endless series. Its limit is the denumerable multitude. The arithm of this multitude is the maximum multitude of the series. If in 2n we substitute the different whole numbers for n, we get an increasing endless series whose limit is the primipostnumeral multitude. Its arithm, which is the maximum multitude of the series, is denumerable only. It is strictly true that the multitude of pack Pn, in the example to which the sophism relates, is 2n. But it is not strictly true that the multitude of Π's in all preceding packs is 2n-1. It happens to be so when n is a number, that is, is enumerable. But strictly it is the multitude next smaller than the multitude of 2n. If the latter is the primipostnumeral multitude, the former can be nothing but the denumerable multitude. This is what we find to be the case, as it must be; and there is nothing paradoxical in it, when rightly understood. There is no value of n for which 2n is denumerable.
The limit of 2n is primipostnumeral. The denumerable is skipped. But were we to reach the denumerable as we may, if we erroneously assume the sum of 2n is 2n-1, when we double that on the principle that 2n = 2×(2n-1), we, of course, only have the denumerable as the result.
214. Let us now consider 22n. Since 2n can never be denumerable, but skips at once from the enumerable to the primipostnumeral, when n is denumerable, it follows that 22n can never be denumerable nor primipostnumeral. For there is no value which 2n could have to make 22n denumerable; and in order that 22n should be primipostnumeral, 2n would have to be denumerable, which is impossible. Thus, 22n skips the denumerable and the denumerable Ed. note, Burks: "primipostnumeral" should replace "denumerable" here multitudes. But if we use square brackets to denote the arithm, so that [2]=2, [3]=3, [∞]=∞, etc., then since 2∞ is denumerable, 22∞ is primipostnumeral.
215. When we start with .0 and .1, and repeating these varieties in the next figures, get .00 .01 .10 .11, and then repeating these varieties in the next figures, get .0000 .0001 etc., and then repeating these varieties in the next figures, get .00000000 .00000001 etc., if we say that, when this operation is carried out until the number of figures is denumerable, we get a primipostnumeral collection, we are assuming what is not true, that by continually doubling an enumerable multitude we shall ever get to a denumerable multitude. That is not true. In that process the denumerable multitude is skipped. We are assuming that because [the] multitude of all the arithmetical places which we pass by is denumerable, when the operation has been performed a denumerable multitude of times, therefore the multitude reached is denumerable. That is, we are confusing 2∞ with [2∞].
The function 22x is no doubt the simplest one which skips the denumerable and primipostnumeral multitudes. Therefore the multitude of this when x is denumerable is, no doubt, the smallest multitude greater than the primipostnumeral multitude. It is the secundopostnumeral multitude.
216. Although there can remain no doubt whatever to an exact logician of the existence in the world of mathematical ideas, of the secundopostnumeral multitude, yet I have been unable, as yet, to form any very intuitionally conception †1 of the construction of such a collection. But I must confess I have not bestowed very much thought upon this matter. I give a few constructions which have occurred to me.
Imagine points on a line to be in one-to-one correspondence with all the different real quantities between 0 and 1. Imagine the line to be repeated over and over again in each repetition having a different set of those points marked. Then the entire collection of repetitions is a secundopostnumeral collection.
Imagine a denumerable row of things, which we may call the B's. Let every set of B's possess some character, which we may call its crane †1 different from the crane of any other set. Imagine a collection of houses which we may call the beths †1 such that each house contains an object corresponding to each crane-character, and according as that object does or does not possess that character, the beth is said to possess or want that character. Then, the different possible varieties of beths, due to their possessing or not possessing the different cranes, form a secundopostnumeral collection.
According to the hypothesis of Euclidean projective geometry there is a plane at infinity. That plane we virtually see when we look up at the blue spread of the sky. A straight line at infinity, although it is straight and looks straight, is called a great semi-circle of the heavens. At two opposite points of the horizon we look at the same point of the plane at infinity. Of course, we cannot look both ways at once. We measure distances on an ordinary straight line by metres and centimetres. We measure distance on a straight line in the sky by degrees and minutes. The entire circuit of the straight line is 180 degrees, and the circuits of all straight lines are equal. But in metres the measure is infinite. If by a projection we make a position of a straight line in the sky correspond to a straight line near at hand, we perhaps make a degree correspond to a metre, although in reality a metre is to a degree in the proportion, 180 degrees to infinity. Imagine that, upon a straight filament in the sky, points are marked off metrically corresponding to all the real quantities. Then let that filament be brought down to earth. If one of those real quantities' points is at any near point, there will not be another at any finite number of kilometres from it. For were there two, when it was in the sky they would have been closer together than any finite fraction of a second of arc. If, however, when you had pulled the filament down from the sky you were to find that each of those things you took for points was really a doubly refracting crystal and that these acted quite independently of one another, so that when you looked through two others you saw four images, when you looked through three you saw eight images, and so on, then if you were to look along the filament through all the crystals, one for each real quantity, the collectum of images you would see would be a secundopostnumeral collection.
217. In like manner, there will be a tertiopostnumeral multitude 222ℵ, a quartopostnumeral multitude 2222ℵ and so on ad infinitum.
All of these will be discrete multitudes although the phenomenon of the incipient cohesion of units becomes more and more marked from one to another.
These multitudes bear no analogy to the orders of infinity of the calculus; for ∞1×∞1 = ∞2. But any of these multiplied by itself gives itself. I had intended to explain these infinites of the calculus. But I find I cannot cram so much into a single lecture.
218. I now inquire, is there any multitude larger than all of these? That there is a multitude greater than any of them is very evident. For every postnumeral multitude has a next greater multitude. Now suppose collections one of each postnumeral multitude, or indeed any denumerable collection of postnumeral multitudes, all unequal. As all of these are possible their aggregate is ipso facto possible. For aggregation is an existential relation, and the aggregate exists (in the only kind of existence we are talking of, existence in the world of noncontradictory ideas) by the very fact that its aggregant parts exist. But this aggregate is no longer a discrete multitude, for the formula 2n>n which I have proved holds for all discrete collections cannot hold for this. In fact writing Exp. n for 2n, (Exp.) ℵℵ is evidently so great that this formula ceases to hold and it represents a collection no longer discrete.
§5. Continua
219. Since then there is a multiplicity or multiplicities greater than any discrete multitude, we have to examine continuous multiplicities. Considered as a mere multitude, we might be tempted to say that continuous multiplicities are incapable of discrimination. For the nature of the differences between them does not depend upon what multitudes enter into the denumerable series of discrete multitudes out of which the continuous multiplicity may be compounded; but it depends on the manner in which they are connected. This connection does not spring from the nature of the individual units, but constitutes the mode of existence of the whole.
The explanation of the paradoxes which arise when you undertake to consider a line or a surface as a collection of points is that, although it is true that a line is nothing but a collection of points of a particular mode of multiplicity, yet in it the individual identities of the units are completely merged, so that not a single one of them can be identified, even approximately, unless it happen to be a topically singular point, that is, either an extremity or a point of branching, in which case there is a defect of continuity at that point. This remark requires explanation, owing to the narrowness of the common ways of conceiving of geometry. Briefly to explain myself, then, geometry or rather mathematical geometry, which deals with pure hypotheses, and unlike physical geometry, does not investigate the properties of objectively valid space — mathematical geometry, I say, consists of three branches; Topics (commonly called Topology), Graphics (or pure projective geometry), and Metrics. But metrics ought not to be regarded as pure geometry. It is the doctrine of the properties of such bodies as have a certain hypothetical property called absolute rigidity, and all such bodies are found to slide upon a certain individual surface called the Absolute. This Absolute, because it possesses individual existence, may properly be called a thing. Metrics, then, is not pure geometry; but is the study of the graphical properties of a certain hypothetical thing. But neither ought graphics to be considered as pure geometry. It is the doctrine of a certain family of surfaces called the planes. But when we ask what surfaces these planes are, we find that no other purely geometrical description can be given of them than that there is a threefold continuum of them and that every three of them have one point and one only in common. But innumerable families of surfaces can be conceived of which that is true. For imagine space to be filled with a fluid and that all the planes, or a sufficient collection of them, are marked by dark films in that fluid. Suppose the fluid to be slightly viscous, so that the different parts of it cannot break away from one another. Then give that fluid any motion. The result will be that those films will be distorted into a vast variety of shapes of all degrees of complexity, and yet any three of them will continue to possess a particle in common. The family of surfaces they then occupy will have every purely geometrical property of the family of planes; and yet they will be planes no longer. The distinguishing character of a plane is that if any particle lying in it be luminous and any filament lying in it be opaque, the shadow of that filament from that luminous particle lies wholly in the plane. Hence it is that unlimited straight lines are called rays. Graphics then is not pure geometry but is geometrical perspective. If, however, any geometer replies that the family of planes ought not to be limited to optical planes, but ought to be considered as any tridimensional continuum of surfaces, any three of which have just one point in common, then my rejoinder is that if we are to allow the planes to undergo any sort of distortion so long as the connections of the different planes of the family are preserved, then the whole doctrine of graphics is manifestly nothing but a branch of topics. For this is just what topics is. It is the study of the continuous connections and defects of continuity of loci which are free to be distorted in any way so long as the integrity of the connections and separations of all their parts is maintained. All strictly pure geometry, therefore, is topics. I now proceed to explain my remark that in a continuous locus no point has any individual identity, unless it be a topically singular point, that is, an isolating point, or either the extremity of a line, or a point from which three or more branches of a line, or two or more sheets of a surface extend. Consider for example an oval line, and let that oval line be broken so as to make a line with two extremities. It may be said that when this happens a point of the oval bursts into two. But I say that there is no particular point of the yet unbroken oval which can be identified, even approximately, with the point which bursts. For to say that the different points of an oval move round the oval, without ever moving out of it, is a form of words entirely destitute of meaning. The points are but places; and the oval and all its parts subsist unchanged whether we regard the points as standing still or running round. In like manner, when we say the oval bursts, we introduce time with a second dimension. Considering the time, the place of the oval is a two dimensional place. This is cylindrical at the bursting and is a ribbon afterward. If one of the dimensions has a different quality from the other, the couple, consisting of a point and instant on the two dimensional continuum where the bursting takes place, has an individual identity. But it cannot be identified with any particular line in the cylindrical part of the two dimensional, even approximately. That line has no individuality.
220. If instead of an oval place, we consider an oval thing, say a filament, then it certainly means something to say that the parts revolve round the oval. For any one particle might be marked black and so be seen to move. And even if it were not actually marked, it would have an individuality which would make it capable of being marked. So that the filament would have a definite velocity of rotation whether it could be seen to move or not. But the reply to this is, that the marking of a single particle would be a discontinuous marking; and if the particles possess all their own individual identities, that is to suppose a discontinuity of existence everywhere, notwithstanding the continuity of place. But I go further. If those particles possess each its individual existence there is a discrete collection of them, and this collection must possess a definite multitude. Now this multitude cannot equal the multiplicity of the aggregate of all possible discrete multitudes; because it is a discrete multitude, and as such it is smaller than another possible multitude. Hence, it is not equal to the multitude of points of the oval. For that is equal to the aggregate of all possible discrete multitudes, since the line, by hypothesis, affords room for any collection of discrete points however great. Hence, if particles of the filament are distributed equally along the line of the oval, there must be, in every sensible part, continuous collections of points, that is, lines, that are unoccupied by particles. These lines may be far less than any assignable magnitudes, that is, far less than any parts into which the system of real quantities enables us to divide the line. But there is no contradiction whatever involved in that. It thus appears that true continuity is logically absolutely repugnant to the individual designation or even approximate individual designation of its units, except at points where the character of the continuity is itself not continuous.
221. In view of what has been said, it is not surprising that those arithmetical operations of addition and multiplication, which seemed to have lost their significance forever, now reappear in reference to continua. It is not that the points, as points, can be one more or less; but if there are defects of continuity, those discontinuities can have perfect individual identity and so be added and multiplied.
222. In regard to lines, there are two kinds of defects of continuity. The first is, that two or more particles moving in a line-figure may be unable to coalesce. The possible number of such non-coalescible particles may be called the chorisis of a figure. Any kind of a geometrical figure has chorisis whether it be a point-figure, a line-figure, a surface-figure, or what. Thus the chorisis of three [not overlapping] ovals is three. The chorisis may be any discrete multitude.
223. The other defect of continuity that can affect a line-figure is that there may be a collection of points upon it from which a particle can move in more or fewer ways than from the generality of points of the figure. These topically singular points, as I call them, are of two kinds: those away from which a particle can move on the line in less than two ways and those from which a particle can move in the line in more than three ways. Of the first kind are, first, isolated points, †1 or topical acnodes, and extremities. Those, from which a particle can move in more than two ways, are points of branching, or topical nodes. The negative of what Listing calls the Census number of a line is, if we give a further extension to his definition, that which I would call the total singularity of the line; namely, it is half the sum of the excesses over two of the number of ways in which a particle could leave the different singular points of the line. No line can have a fractional total singularity.
224. In regard to surfaces, the chorisis is very simple and calls for no particular attention.
The theory of the singular places of surfaces is somewhat complicated. The singular places may be points, and those are either isolated points or points where two or more sheets are tacked together. Or the singular places may be isolated lines, and those are either totally isolated, or they may cut the surface. Such lines can have singularities like lines generally. Or the singular places may be lines which are either bounding edges or lines of splitting of the surface, or they may be in some parts edges and in other parts lines of splitting. They have singular points at which the line need not branch. All that is necessary is that the identities of the sheets that join there should change. If such a line has an extremity or point of odd branches, an even number of the sheets which come together there must change.
225. In addition to that, surfaces are another kind of defect of continuity, which Listing calls their cyclosis. That is, there is room upon them for oval filaments which cannot shrink to nothing by any movement in the surface. The number of operations each of a kind calculated to destroy a simple cyclosis which have to be [employed] in order to destroy the cyclosis of a surface is the number of the cyclosis. A puncture of a surface which does not change it from a closed surface to an open surface increases the cyclosis by one. A cut from edge to edge which does not increase the chorisis diminishes the cyclosis by one.
The cyclosis of a spherical surface is 0; that of an unlimited plane is 1; that of an anchor-ring is 2, that of a plane with a fornix (or bridge from one part to another) is 3; that of an anchor-ring with a fornix is 4, etc.
Euler's theorem †1 concerning polyhedra is an example of the additive arithmetic of continua.
226. The multiplicity of points upon a surface must be admitted, as it seems to me, to be the square of that of the points of a line, and so with higher dimensions. The multitude of dimensions may be of any discrete multitude.
Paper 7: The Simplest MathematicsP †1
§1. The Essence of Mathematics
227. In this chapter, I propose to consider certain extremely simple branches of mathematics which, owing to their utility in logic, have to be treated in considerable detail, although to the mathematician they are hardly worth consideration. In Chapter 4, †2 I shall take up those branches of mathematics upon which the interest of mathematicians is centred, but shall do no more than make a rapid examination of their logical procedure. In Chapter 5, †2 I shall treat formal logic by the aid of mathematics. There can really be little logical matter in these chapters; but they seem to me to be quite indispensable preliminaries to the study of logic.
228. It does not seem to me that mathematics depends in any way upon logic. It reasons, of course. But if the mathematician ever hesitates or errs in his reasoning, logic cannot come to his aid. He would be far more liable to commit similar as well as other errors there. On the contrary, I am persuaded that logic cannot possibly attain the solution of its problems without great use of mathematics. Indeed all formal logic is merely mathematics applied to logic. †3
229. It was Benjamin Peirce, †4 whose son I boast myself, that in 1870 first defined mathematics as "the science which draws necessary conclusions." †5 This was a hard saying at the time; but today, students of the philosophy of mathematics generally acknowledge its substantial correctness.
230. The common definition, among such people as ordinary schoolmasters, still is that mathematics is the science of quantity. As this is inevitably understood in English, it seems to be a misunderstanding of a definition which may be very old, †P1 the original meaning being that mathematics is the science of quantities, that is, forms possessing quantity. We perceive that Euclid was aware that a large branch of geometry had nothing to do with measurement (unless as an aid in demonstrating); and, therefore, a Greek geometer of his age (early in the third century B.C.) or later could not define mathematics as the science of that which the abstract noun quantity expresses. A line, however, was classed as a quantity, or quantum, by Aristotle †1 and his followers; so that even perspective (which deals wholly with intersections and projections, not at all with lengths) could be said to be a science of quantities, "quantity" being taken in the concrete sense. That this was what was originally meant by the definition "Mathematics is the science of quantity," is sufficiently shown by the circumstance that those writers who first enunciate it, about A.D. 500, that is Ammonius Hermiæ †2 and Boëthius, †3 make astronomy and music branches of mathematics; and it is confirmed by the reasons they give for doing so. †P2 Even Philo of Alexandria (100 B.C.), who defines mathematics as the science of ideas furnished by sensation and reflection in respect to their necessary consequences, since he includes under mathematics, besides its more essential parts, the theory of numbers and geometry, also the practical arithmetic of the Greeks, geodesy, mechanics, optics (or projective geometry), music, and astronomy, must be said to take the word 'mathematics' in a different sense from ours. That Aristotle did not regard mathematics as the science of quantity, in the modern abstract sense, is evidenced in various ways. The subjects of mathematics are, according to him, the how much and the continuous. (See Metaph. K iii 1061 a 33). He referred the continuous to his category of quantum; and therefore he did make quantum, in a broad sense, the one object of mathematics.
231. Plato, in the Sixth book of the Republic, †P1 holds that the essential characteristic of mathematics lies in the peculiar kind and degree of its abstraction, greater than that of physics but less than that of what we now call philosophy; and Aristotle †1 follows his master in this definition. It has ever since been the habit of metaphysicians to extol their own reasonings and conclusions as vastly more abstract and scientific than those of mathematics. It certainly would seem that problems about God, Freedom, and Immortality are more exalted than, for example, the question how many hours, minutes, and seconds would elapse before two couriers travelling under assumed conditions will come together; although I do not know that this has been proved. But that the methods of thought of the metaphysicians are, as a matter of historical fact, in any aspect, not far inferior to those of mathematics is simply an infatuation. One singular consequence of the notion which prevailed during the greater part of the history of philosophy, that metaphysical reasoning ought to be similar to that of mathematics, only more so, has been that sundry mathematicians have thought themselves, as mathematicians, qualified to discuss philosophy; and no worse metaphysics than theirs is to be found.
232. Kant †2 regarded mathematical propositions as synthetical judgments a priori; wherein there is this much truth, that they are not, for the most part, what he called analytical judgments; that is, the predicate is not, in the sense he intended, contained in the definition of the subject. But if the propositions of arithmetic, for example, are true cognitions, or even forms of cognition, this circumstance is quite aside from their mathematical truth. For all modern mathematicians agree with Plato and Aristotle that mathematics deals exclusively with hypothetical states of things, and asserts no matter of fact whatever; and further, that it is thus alone that the necessity of its conclusions is to be explained. †P1 This is the true essence of mathematics; and my father's definition is in so far correct that it is impossible to reason necessarily concerning anything else than a pure hypothesis. Of course, I do not mean that if such pure hypothesis happened to be true of an actual state of things, the reasoning would thereby cease to be necessary. Only, it never would be known apodictically to be true of an actual state of things. Suppose a state of things of a perfectly definite, general description. That is, there must be no room for doubt as to whether anything, itself determinate, would or would not come under that description. And suppose, further, that this description refers to nothing occult — nothing that cannot be summoned up fully into the imagination. Assume, then, a range of possibilities equally definite and equally subject to the imagination; so that, so far as the given description of the supposed state of things is general, the different ways in which it might be made determinate could never introduce doubtful or occult features. The assumption, for example, must not refer to any matter of fact. For questions of fact are not within the purview of the imagination. Nor must it be such that, for example, it could lead us to ask whether the vowel OO can be imagined to be sounded on as high a pitch as the vowel EE. Perhaps it would have to be restricted to pure spatial, temporal, and logical relations. Be that as it may, the question whether in such a state of things, a certain other similarly definite state of things, equally a matter of the imagination, could or could not, in the assumed range of possibility, ever occur, would be one in reference to which one of the two answers, Yes and No, would be true, but never both. But all pertinent facts would be within the beck and call of the imagination; and consequently nothing but the operation of thought would be necessary to render the true answer. Nor, supposing the answer to cover the whole range of possibility assumed, could this be rendered otherwise than by reasoning that would be apodictic, general, and exact. No knowledge of what actually is, no positive knowledge, as we say, could result. On the other hand, to assert that any source of information that is restricted to actual facts could afford us a necessary knowledge, that is, knowledge relating to a whole general range of possibility, would be a flat contradiction in terms.
233. Mathematics is the study of what is true of hypothetical states of things. That is its essence and definition. Everything in it, therefore, beyond the first precepts for the construction of the hypotheses, has to be of the nature of apodictic inference. No doubt, we may reason imperfectly and jump at a conclusion; still, the conclusion so guessed at is, after all, that in a certain supposed state of things something would necessarily be true. Conversely, too, every apodictic inference is, strictly speaking, mathematics. But mathematics, as a serious science, has, over and above its essential character of being hypothetical, an accidental characteristic peculiarity — a proprium, as the Aristotelians used to say — which is of the greatest logical interest. Namely, while all the "philosophers" follow Aristotle in holding no demonstration to be thoroughly satisfactory except what they call a "direct" demonstration, or a "demonstration why" — by which they mean a demonstration which employs only general concepts and concludes nothing but what would be an item of a definition if all its terms were themselves distinctly defined — the mathematicians, on the contrary, entertain a contempt for that style of reasoning, and glory in what the philosophers stigmatize as "mere" indirect demonstrations, or "demonstrations that." Those propositions which can be deduced from others by reasoning of the kind that the philosophers extol are set down by mathematicians as "corollaries." That is to say, they are like those geometrical truths which Euclid did not deem worthy of particular mention, and which his editors inserted with a garland, or corolla, against each in the margin, implying perhaps that it was to them that such honor as might attach to these insignificant remarks was due. In the theorems, or at least in all the major theorems, a different kind of reasoning is demanded. Here, it will not do to confine oneself to general terms. It is necessary to set down, or to imagine, some individual and definite schema, or diagram — in geometry, a figure composed of lines with letters attached; in algebra an array of letters of which some are repeated. This schema is constructed so as to conform to a hypothesis set forth in general terms in the thesis of the theorem. Pains are taken so to construct it that there would be something closely similar in every possible state of things to which the hypothetical description in the thesis would be applicable, and furthermore to construct it so that it shall have no other characters which could influence the reasoning. How it can be that, although the reasoning is based upon the study of an individual schema, it is nevertheless necessary, that is, applicable, to all possible cases, is one of the questions we shall have to consider. Just now, I wish to point out that after the schema has been constructed according to the precept virtually contained in the thesis, the assertion of the theorem is not evidently true, even for the individual schema; nor will any amount of hard thinking of the philosophers' corollarial kind ever render it evident. Thinking in general terms is not enough. It is necessary that something should be DONE. In geometry, subsidiary lines are drawn. In algebra permissible transformations are made. Thereupon, the faculty of observation is called into play. Some relation between the parts of the schema is remarked. But would this relation subsist in every possible case? Mere corollarial reasoning will sometimes assure us of this. But, generally speaking, it may be necessary to draw distinct schemata to represent alternative possibilities. Theorematic reasoning invariably depends upon experimentation with individual schemata. We shall find that, in the last analysis, the same thing is true of the corollarial reasoning, too; even the Aristotelian "demonstration why." Only in this case, the very words serve as schemata. Accordingly, we may say that corollarial, or "philosophical" reasoning is reasoning with words; while theorematic, or mathematical reasoning proper, is reasoning with specially constructed schemata.
234. Another characteristic of mathematical thought is the extraordinary use it makes of abstractions. Abstractions have been a favorite butt of ridicule in modern times. Now it is very easy to laugh at the old physician who is represented as answering the question, why opium puts people to sleep, by saying that it is because it has a dormative virtue. It is an answer that no doubt carries vagueness to its last extreme. Yet, invented as the story was to show how little meaning there might be in an abstraction, nevertheless the physician's answer does contain a truth that modern philosophy has generally denied: it does assert that there really is in opium something which explains its always putting people to sleep. This has, I say, been denied by modern philosophers generally. Not, of course, explicitly; but when they say that the different events of people going to sleep after taking opium have really nothing in common, but only that the mind classes them together — and this is what they virtually do say in denying the reality of generals — they do implicitly deny that there is any true explanation of opium's generally putting people to sleep.
235. Look through the modern logical treatises, and you will find that they almost all fall into one or other of two errors, as I hold them to be; that of setting aside the doctrine of abstraction (in the sense in which an abstract noun marks an abstraction) as a grammatical topic with which the logician need not particularly concern himself; and that of confounding abstraction, in this sense, with that operation of the mind by which we pay attention to one feature of a percept to the disregard of others. The two things are entirely disconnected. The most ordinary fact of perception, such as "it is light," involves precisive abstraction, or prescission. †1 But hypostatic abstraction, the abstraction which transforms "it is light" into "there is light here," which is the sense which I shall commonly attach to the word abstraction (since prescission will do for precisive abstraction) is a very special mode of thought. It consists in taking a feature of a percept or percepts (after it has already been prescinded from the other elements of the percept), so as to take propositional form in a judgment (indeed, it may operate upon any judgment whatsoever), and in conceiving this fact to consist in the relation between the subject of that judgment and another subject, which has a mode of being that merely consists in the truth of propositions of which the corresponding concrete term is the predicate. Thus, we transform the proposition, "honey is sweet," into "honey possesses sweetness." "Sweetness" might be called a fictitious thing, in one sense. But since the mode of being attributed to it consists in no more than the fact that some things are sweet, and it is not pretended, or imagined, that it has any other mode of being, there is, after all, no fiction. The only profession made is that we consider the fact of honey being sweet under the form of a relation; and so we really can. I have selected sweetness as an instance of one of the least useful of abstractions. Yet even this is convenient. It facilitates such thoughts as that the sweetness of honey is particularly cloying; that the sweetness of honey is something like the sweetness of a honeymoon; etc. Abstractions are particularly congenial to mathematics. Everyday life first, for example, found the need of that class of abstractions which we call collections. Instead of saying that some human beings are males and all the rest females, it was found convenient to say that mankind consists of the male part and the female part. The same thought makes classes of collections, such as pairs, leashes, quatrains, hands, weeks, dozens, baker's dozens, sonnets, scores, quires, hundreds, long hundreds, gross, reams, thousands, myriads, lacs, millions, milliards, milliasses, etc. These have suggested a great branch of mathematics. †P1 Again, a point moves: it is by abstraction that the geometer says that it "describes a line." This line, though an abstraction, itself moves; and this is regarded as generating a surface; and so on. So likewise, when the analyst treats operations as themselves subjects of operations, a method whose utility will not be denied, this is another instance of abstraction. Maxwell's notion of a tension exercised upon lines of electrical force, transverse to them, is somewhat similar. These examples exhibit the great rolling billows of abstraction in the ocean of mathematical thought; but when we come to a minute examination of it, we shall find, in every department, incessant ripples of the same form of thought, of which the examples I have mentioned give no hint.
236. Another characteristic of mathematical thought is that it can have no success where it cannot generalize. One cannot, for example, deny that chess is mathematics, after a fashion; but, owing to the exceptions which everywhere confront the mathematician in this field — such as the limits of the board; the single steps of king, knight, and pawn; the finite number of squares; the peculiar mode of capture by pawns; the queening of pawns; castling — there results a mathematics whose wings are effectually clipped, and which can only run along the ground. Hence it is that a mathematician often finds what a chess-player might call a gambit to his advantage; exchanging a smaller problem that involves exceptions for a larger one free from them. Thus, rather than suppose that parallel lines, unlike all other pairs of straight lines in a plane, never meet, he supposes that they intersect at infinity. Rather than suppose that some equations have roots while others have not, he supplements real quantity by the infinitely greater realm of imaginary quantity. He tells us with ease how many inflexions a plane curve of any description has; but if we ask how many of these are real, and how many merely fictional, he is unable to say. He is perplexed by three-dimensional space, because not all pairs of straight lines intersect, and finds it to his advantage to use quaternions which represent a sort of four-fold continuum, in order to avoid the exception. It is because exceptions so hamper the mathematician that almost all the relations with which he chooses to deal are of the nature of correspondences; that is to say, such relations that for every relate there is the same number of correlates, and for every correlate the same number of relates.
237. Among the minor, yet striking characteristics of mathematics, may be mentioned the fleshless and skeletal build of its propositions; the peculiar difficulty, complication, and stress of its reasonings; the perfect exactitude of its results; their broad universality; their practical infallibility. It is easy to speak with precision upon a general theme. Only, one must commonly surrender all ambition to be certain. It is equally easy to be certain. One has only to be sufficiently vague. It is not so difficult to be pretty precise and fairly certain at once about a very narrow subject. But to reunite, like mathematics, perfect exactitude and practical infallibility with unrestricted universality, is remarkable. But it is not hard to see that all these characters of mathematics are inevitable consequences of its being the study of hypothetical truth.
238. It is difficult to decide between the two definitions of mathematics; the one by its method, that of drawing necessary conclusions; the other by its aim and subject matter, as the study of hypothetical states of things. The former makes or seems to make the deduction of the consequences of hypotheses the sole business of the mathematician as such. But it cannot be denied that immense genius has been exercised in the mere framing of such general hypotheses as the field of imaginary quantity and the allied idea of Riemann's surface, in imagining non-Euclidian measurement, ideal numbers, the perfect liquid. Even the framing of the particular hypotheses of special problems almost always calls for good judgment and knowledge, and sometimes for great intellectual power, as in the case of Boole's logical algebra. Shall we exclude this work from the domain of mathematics? Perhaps the answer should be that, in the first place, whatever exercise of intellect may be called for in applying mathematics to a question not propounded in mathematical form [it] is certainly not pure mathematical thought; and in the second place, that the mere creation of a hypothesis may be a grand work of poietic †1 genius, but cannot be said to be scientific, inasmuch as that which it produces is neither true nor false, and therefore is not knowledge. This reply suggests the further remark that if mathematics is the study of purely imaginary states of things, poets must be great mathematicians, especially that class of poets who write novels of intricate and enigmatical plots. Even the reply, which is obvious, that by studying imaginary states of things we mean studying what is true of them, perhaps does not fully meet the objection. The article Mathematics in the ninth edition of the Encyclopaedia Britannica †2 makes mathematics consist in the study of a particular sort of hypotheses, namely, those that are exact, etc., as there set forth at some length. The article is well worthy of consideration.
239. The philosophical mathematician, Dr. Richard Dedekind, †3 holds mathematics to be a branch of logic. This would not result from my father's definition, which runs, not that mathematics is the science of drawing necessary conclusions — which would be deductive logic — but that it is the science which draws necessary conclusions. It is evident, and I know as a fact, that he had this distinction in view. At the time when he thought out this definition, he, a mathematician, and I, a logician, held daily discussions about a large subject which interested us both; and he was struck, as I was, with the contrary nature of his interest and mine in the same propositions. The logician does not care particularly about this or that hypothesis or its consequences, except so far as these things may throw a light upon the nature of reasoning. The mathematician is intensely interested in efficient methods of reasoning, with a view to their possible extension to new problems; but he does not, quâ mathematician, trouble himself minutely to dissect those parts of this method whose correctness is a matter of course. The different aspects which the algebra of logic will assume for the two men is instructive in this respect. The mathematician asks what value this algebra has as a calculus. Can it be applied to unravelling a complicated question? Will it, at one stroke, produce a remote consequence? The logician does not wish the algebra to have that character. On the contrary, the greater number of distinct logical steps, into which the algebra breaks up an inference, will for him constitute a superiority of it over another which moves more swiftly to its conclusions. He demands that the algebra shall analyze a reasoning into its last elementary steps. Thus, that which is a merit in a logical algebra for one of these students is a demerit in the eyes of the other. The one studies the science of drawing conclusions, the other the science which draws necessary conclusions.
240. But, indeed, the difference between the two sciences is far more than that between two points of view. Mathematics is purely hypothetical: it produces nothing but conditional propositions. Logic, on the contrary, is categorical in its assertions. True, it is not merely, or even mainly, a mere discovery of what really is, like metaphysics. It is a normative science. It thus has a strongly mathematical character, at least in its methodeutic division; for here it analyzes the problem of how, with given means, a required end is to be pursued. This is, at most, to say that it has to call in the aid of mathematics; that it has a mathematical branch. But so much may be said of every science. There is a mathematical logic, just as there is a mathematical optics and a mathematical economics. Mathematical logic is formal logic. Formal logic, however developed, is mathematics. Formal logic, however, is by no means the whole of logic, or even its principal part. It is hardly to be reckoned as a part of logic proper. Logic has to define its aim; and in doing so is even more dependent upon ethics, †1 or the philosophy of aims, by far, than it is, in the methodeutic branch, upon mathematics. We shall soon come to understand how a student of ethics might well be tempted to make his science a branch of logic; as, indeed, it pretty nearly was in the mind of Socrates. But this would be no truer a view than the other. Logic depends upon mathematics; still more intimately upon ethics; but its proper concern is with truths beyond the purview of either.
241. There are two characters of mathematics which have not yet been mentioned, because they are not exclusive characteristics of it. One of these, which need not detain us, is that mathematics is distinguished from all other sciences †2 except only ethics, in standing in no need of ethics. Every other science, even logic — logic, especially — is in its early stages in danger of evaporating into airy nothingness, degenerating, as the Germans say, into an anachrioid [?] film, spun from the stuff that dreams are made of. There is no such danger for pure mathematics; for that is precisely what mathematics ought to be.
242. The other character — and of particular interest it is to us just now — is that mathematics, along with ethics and logic alone of the sciences, has no need of any appeal to logic. No doubt, some reader may exclaim in dissent to this, on first hearing it said. Mathematics, they may say, is preëminently a science of reasoning. So it is; preëminently a science that reasons. But just as it is not necessary, in order to talk, to understand the theory of the formation of vowel sounds, so it is not necessary, in order to reason, to be in possession of the theory of reasoning. Otherwise, plainly, the science of logic could never be developed. The contrary objection would have more excuse, that no science stands in need of logic, since our natural power of reason is enough. Make of logic what the majority of treatises in the past have made of it, and a very common class of English and French books still make of it — that is to say, mainly formal logic, and that formal logic represented as an art of reasoning — and in my opinion this objection is more than sound, for such logic is a great hindrance to right reasoning. It would, however, be aside from our present purpose to examine this objection minutely. I will content myself with saying that undoubtedly our natural power of reasoning is enough, in the same sense that it is enough, in order to obtain a wireless transatlantic telegraph, that men should be born. That is to say, it is bound to come sooner or later. But that does not make research into the nature of electricity needless for gaining such a telegraph. So likewise if the study of electricity had been pursued resolutely, even if no special attention had ever been paid to mathematics, the requisite mathematical ideas would surely have been evolved. Faraday, indeed, did evolve them without any acquaintance with mathematics. Still it would be far more economical to postpone electrical researches, to study mathematics by itself, and then to apply it to electricity, which was Maxwell's way. In this same manner, the various logical difficulties which arise in the course of every science except mathematics, ethics, and logic, will, no doubt, get worked out after a time, even though no special study of logic be made. But it would be far more economical to make first a systematic study of logic. If anybody should ask what are these logical difficulties which arise in all the sciences, he must have read the history of science very irreflectively. What was the famous controversy concerning the measure of force but a logical difficulty? What was the controversy between the uniformitarians and the catastrophists but a question of whether or not a given conclusion followed from acknowledged premisses? This will fully appear in the course of our studies in the present work. †1
243. But it may be asked whether mathematics, ethics, and logic have not encountered similar difficulties. Are the doctrines of logic at all settled? Is the history of ethics anything but a history of controversy? Have no logical errors been committed by mathematicians? To that I reply, first, as to logic, that not only have the rank and file of writers on the subject been, as an eminent psychiatrist, Maudsley, declares, men of arrested brain-development, and not only have they generally lacked the most essential qualification for the study, namely mathematical training, but the main reason why logic is unsettled is that thirteen different opinions are current as to the true aim of the science. †1 Now this is not a logical difficulty but an ethical difficulty; for ethics is the science of aims. Secondly, it is true that pure ethics has been, and always must be, a theatre of discussion, for the reason that its study consists in the gradual development of a distinct recognition of a satisfactory aim. It is a science of subtleties, no doubt; but it is not logic, but the development of the ideal, which really creates and resolves the problems of ethics. Thirdly, in mathematics errors of reasoning have occurred, nay, have passed unchallenged for thousands of years. This, however, was simply because they escaped notice. Never, in the whole history of the science, has a question whether a given conclusion followed mathematically from given premisses, when once started, failed to receive a speedy and unanimous reply. Very few have been even the apparent exceptions; and those few have been due to the fact that it is only within the last half century that mathematicians have come to have a perfectly clear recognition of what is mathematical soil and what foreign to mathematics. Perhaps the nearest approximation to an exception was the dispute about the use of divergent series. Here neither party was in possession of sufficient pure mathematical reasons covering the whole ground; and such reasons as they had were not only of an extra-mathematical kind, but were used to support more or less vague positions. It appeared then, as we all know now, that divergent series are of the utmost utility. †P1
Struck by this circumstance, and making an inference, of which it is sufficient to say that it was not mathematical, many of the old mathematicians pushed the use of divergent series beyond all reason. This was a case of mathematicians disputing about the validity of a kind of inference that is not mathematical. No doubt, a sound logic (such as has not hitherto been developed) would have shown clearly that that non-mathematical inference was not a sound one. But this is, I believe, the only instance in which any large party in the mathematical world ever proposed to rely, in mathematics, upon unmathematical reasoning. My proposition is that true mathematical reasoning is so much more evident than it is possible to render any doctrine of logic proper — without just such reasoning — that an appeal in mathematics to logic could only embroil a situation. On the contrary, such difficulties as may arise concerning necessary reasoning have to be solved by the logician by reducing them to questions of mathematics. Upon those mathematical dicta, as we shall come clearly to see, the logician has ultimately to repose.
244. So a double motive induces me to devote some preliminary chapters to mathematics. For, in the first place, in studying the theory of reasoning, we are concerned to acquaint ourselves with the methods of that prior science of which acts of reasoning form the staple. In the second place, logic, like any other science, has its mathematical department, and of that, a large portion, at any rate, may with entire convenience be studied as soon as we take up the study of logic, without any propedeutic. That portion is what goes by the name of Formal Logic. †P1 It so happens that the special kind of mathematics needed for formal logic, which, therefore, we need to study in detail, as we need not study other branches of mathematics, is so excessively simple as neither to have much mathematical interest, nor to display the peculiarities of mathematical reasoning. I shall, therefore, devote the present chapter — a very dull one, I am sorry to say, it must be — to this kind of mathematics. Chapter 4 will treat of the more truly mathematical mathematics; and Chapter 5 will apply the results of the present chapter to the study of Formal Logic. †1
§2. Division of Pure MathematicsP
245. We have to make a rapid survey of pure mathematics, in so far as it interests us as students of logic. Each branch of mathematics will have to be reconnoitered and its methods examined. Those parts of the calculus of which use has to be made in the study of reasoning must receive a fuller treatment. Finally, having so collected some information about mathematics, we may venture upon some useful generalizations concerning the nature of mathematical thought. But this plan calls for a preliminary dissection of mathematics into its several branches.
246. Each branch of mathematics sets out from a general hypothesis of its own. I mean by its general hypothesis the substance of its postulates and axioms, and even of its definitions, should they be contaminated with any substance, instead of being the pure verbiage they ought to be. We have to make choice, then, between a division of mathematics according to the matter of its hypotheses, or according to the forms of the schemata of which it avails itself. These latter are either geometrical or algebraical. Geometrical schemata are linear figures with letters attached; the perfect imaginability, on the one hand, and the extreme familiarity, on the other hand, of spatial relations are taken advantage of, to enable us to see what will necessarily be true under supposed conditions. The algebraical schemata are arrays of characters, sometimes in series, sometimes in blocks, with which are associated certain rules of permissible transformation. With these rules the algebraist has perfectly to familiarize himself. By virtue of these rules, become habits of association, when one array has been written or assumed to be permissibly scriptible, the mathematician just as directly perceives that another array is permissibly scriptible, as he perceives that a person talking in a certain tone is angry, or [is] using certain words in such and such a sense.
247. The primary division of mathematics into algebra and geometry is the usual one. But, in all departments, it appears both a priori and a posteriori, that divisions according to differences of purpose should be given a higher rank than divisions according to different methods of attaining that purpose. †1 The division of pure mathematics into algebra and geometry was first adopted before the modern conception of pure mathematics had been distinctly prescinded, and when geometry and algebra seemed to deal with different subjects. It remains, a vestige of that old unclearness and a witness that not even mathematicians are able entirely to shake off the sequelæ of exploded ideas. For now that everybody knows that any mathematical subject, from the theory of numbers to topical geometry, may be treated either algebraically or geometrically, one cannot fail to see that so to divide mathematics is to make twice over the division according to fundamental hypotheses, to which one must come, at last. This duplication is worse than useless, since the geometrical and algebraical methods are by many writers continually mixed. No such inconvenience attends the other plan of classification; for two sets of fundamental hypotheses could not, properly speaking, be mixed without self-contradiction.
248. Let us, then, divide mathematics according to the nature of its general hypotheses, taking for the ground of primary division the multitude of units, or elements, that are supposed; and for the ground of subdivision that mode of relationship between the elements upon which the hypotheses focus the attention.
249. From a logician's point of view this plan of classification would seem to call for a preliminary analysis of what is meant by multitude. But to execute this analysis satisfactorily, considerable studies of logic would be indispensable preliminaries. Besides, it is not at all in the spirit of mathematics to analyze the ideas with which it works farther than is needful for using them in deducing consequences, nor sooner than that need comes to be felt. It is true that we, as students of logic, are not bound to embrace the mathematical ways of thought as far as that, but the other circumstance, that it is, at the present stage of our studies, impossible to make the analysis, must be conclusive.
§3. The Simplest Branch of MathematicsP
250. Were nothing at all supposed, mathematics would have no ground at all to go upon. Were the hypothesis merely that there was nothing but one unit, there would not be a possibility of a question, since only one answer would be possible. Consequently, the simplest possible hypothesis is that there are two objects, which we may denote by v and f. Then the first kind of problem of this algebra will be, given certain data concerning an unknown object, x, required to know whether it is v or f. Or similar problems may arise concerning several unknowns, x, y, etc. Or when the last problem cannot be resolved, we may ask whether, supposing x to be v, will y be v or f? And similarly, supposing x to be f. Again, given certain data concerning x, we may ask, what else needs to be known in order to compel x to be v or to be f. Or again, given certain information about x, y, and z, what relations between x and z remain unchanged whether y be v or f?
251. Let us call v and f the two possible values, one of which must be attached to any unknown. For the form of reasoning will be the same whether we talk of identity or attachment. The attachment may be of any kind so long as each unknown must be, or be attached to, v or f, but cannot be or be attached to, both v and f. This idea of a system of values is one of the most fundamental abstractions of the algebraic method of mathematics. An object of the universe, whose value is generally unknown, though it may in special cases be known — that is to say, an object which, to phrase the matter differently, is one of the values, though perhaps we do not know which — is called, when we speak of it as "having" a value, a quantity. For example, suppose the problem under consideration be to determine, upon a certain hypothesis, the numerical definition of the instant, or, as we may say, to determine the exact date, at which two couriers will meet. This date is some one of the series of numbers each of which is expressible, at least to any predesignate degree of approximation, in our usual method of numeral notation. That series of numbers will be the system of values; and the number we want is one of them. But we find it convenient to use a different phrase, and to say that the date is defined to be the date at which the couriers meet, that this fixes its identity, and that what we seek to know is what value becomes attached to it in consequence of the conditions the problem supposes. It will be convenient to conceive of this statement as a "mere" variation of phraseology, although, as we shall learn, the word "mere" in such cases is often inappropriate, since great mathematical results are attainable by such means. Dichotomic algebra can be applied wherever there are just two possible alternatives. Thus, we might call the v the truth, and f falsity. Then, in regard to a given proposition we may seek to know whether it is true or false; that is, whether it is or is not a partial description of the real universe, or say, whether what it means is identical with the existent truth or identical with nothing. Looking at the matter in a different way, or phrasing it differently, we say that a proposition has one or other of two values, being either true and good for something, or false and good for nothing. The point of view of mathematics is the point of view which looks upon those two points of view as no more than different phrases for the same fact.
252. There is another little group of algebraical words which must now be defined in the imperfect way in which they can be defined for dichotomic mathematics. In the first place, there are the pair of terms, constant, or constant quantity, and variable, or variable quantity. These words were introduced by the Marquis d'Hôpital †1 in 1696. Suppose two couriers to set out, at the same instant, from two points 12 miles apart and to travel toward one another, the one at the rate of 7 miles an hour, the other at the rate of 8 miles an hour: when will they meet? They evidently approach one another at the rate of 7 plus 8, or 15 miles an hour; and they will reduce the distance of 12 miles to nothing in 12/15 of an hour, or 12 times 4, or 48, minutes. But suppose we find the distance was wrongly given; that it is 12 1/2 miles. Then, the date, or numerical designation of the instant of meeting, becomes different. But if we choose to say that the quantity sought is defined as the time of meeting, and that it remains the same quantity, having the same definition, but that its value only is altered, then that quantity is said to be variable. A quantity is said to be variable when we propose to consider it as taking different values in different states of things; or, to phrase the matter differently, when we consider a group of questions together, as one general question, the single questions having different values for their answers. The most usual case is where we suppose the quantity to take all possible values under different circumstances. A quantity is called constant when the hypothesis includes no states of things in which its value changes. The difference between an unknown quantity and a variable quantity is trifling. The unknown quantity is variable at first; but special hypotheses being adopted, it is restricted to certain values, perhaps to a single value.
253. The word function (a sort of semi-synonym of "operation") was first used in something like its present mathematical sense in 1692, by a writer who was doubtless Leibniz. †1 It soon came into use with the circle of analysts of whom Leibniz was the centre. But the first attempt at a definition of it was by John Bernouilli, †2 in 1718. There has since been much discussion as to what precise meaning can most advantageously be applied to it; but the most general definition, that of Dirichlet, †3 is confined to a system of numerical values. Since I wish to apply the word to all sorts of algebra, I shall, under these circumstances, take the liberty of generalizing the meaning in the manner which seems to me to be called for. I shall say then, that, given two ordered sets of the same number of quantities, x1, x2, x3, . . . xn, and y1, y2, y3 . . . yn, any quantity, say x2, of the one set is the same function of the other quantities of that same set, which are called its arguments, that the corresponding quantity, y2, according to the order of arrangement of the other set, is of the remaining quantities of that set, if and only if every set of values which either set of quantities, in their order, can take, can likewise be taken by the other set. Thus, to say that a quantity is a given function of certain quantities as arguments is simply to say that its value stands in a given relation to theirs; or that a given proposition is true of the whole set of values in their order. To say simply that one quantity is some function of certain others is to say nothing; since of every set of values something is true. But this no more renders function a useless word than the fact, that it means nothing to say of a set of things that there is some relation between them, renders relation a useless word.
I may mention that the old and usual expression is "a function of variables"; but the word argument here is not unusual and is more explicit. The function is also called the dependent variable; the arguments, the independent variables. Of course, any one of the whole set of quantities composed of the function and its arguments is just as dependent as any other. It is a mere way of referring to them. The function is often conceived, very conveniently, as resulting from an operation performed on the arguments, which are then called operands. The idea is that the definition of the same function implies a rule which permits such sets of values as may conform to its conditions and excludes others; and the operation is the operation of actually applying this rule, when the values of all the quantities but one are given, in order to ascertain what the value of the remaining quantity can be.
254. Among functions, or operations, there is one extensive class which is of particular importance. I call it the class of correspondential functions, or operations. Namely, if all the variables but one, independent and dependent, have a set of values assigned to them, then, if the relation between them is a correspondence, the number of different values which the remaining variable can have, is generally the same, whatever the particular set of assigned values may be; although this number is not necessarily the same when different quantities are thus left over to the last. I say generally the same, because there may be peculiar isolated exceptions, though this limitation can have no significance in dichotomic mathematics. A function which is in correspondence with its arguments may be called a correspondential function. It may be remarked that it is not the habit of mathematicians, in general statements, to pay attention to isolated exceptions; and when a mathematician uses the phrase "in general" he means to be understood as not considering possible peculiar cases. Thus, I have known a great mathematician to enunciate a proposition concerning multiple algebra to be true "in general" when the state of the case was that there were just two instances of its being true against an infinity of instances of its being false.
255. A function which has but one value for any one set of values of the arguments is called monotropic. A function which, when all the arguments except a certain one take any fixed values, always changes its value with a change of that one, may be called distinctive for that argument.
256. If the relation between a function and its arguments is such that one of the latter may take any value for every set of the values of the others without altering the function, the function may be said to be invariable with that argument. If the function can take any value, whatever values be assigned to the arguments, it may be said to be independent of the arguments. In either of these cases, the function may be called a degenerate function.
257. With this lexical preface, we come down to our dichotomic mathematics, which I shall treat algebraically. The first thing to be done is to fix upon a sign to show that any quantity, say x, has the value v, and upon another to signify that it has the value f. The simplest suggestion is that universally used since man began to keep accounts; namely, to appropriate a place in which we are to write whatever is v, say the upper of two lines, the lower of which is appropriated to quantities whose value is f. That is, we open one account for v, and another for f. In doing this, we put v and f in a radically different category from the other letters, very much as two opposite qualities, say good and bad, are attributed to concrete objects. I do not mean that there is any other analogy than that the values, v and f, are made to be of a different nature from the quantities, x, y, z, etc. One or other of the values, but not both, is connected, in some definite sense, and it matters not what the sense may be, so long as it is definite, with each quantity. But here an important remark obtrudes. Non-connection in any definite way is only another equally definite mode of connection; especially in a strictly dichotomic state of things. If, for example, every man either does good and eschews evil, or does evil and eschews good, then the former is thereby connected with evil by eschewing it, as he is connected with good in the mode of connection called doing it. Note how the perfect balance of our initial dichotomy generates new dichotomies: first, two categories, those of value and of quantity; then, two modes of connection between a value and a quantity.
258. Let us modify our mode of signifying the attachment of a quantity to a value, so as to show its contrary attachment to the opposite value. For this purpose,
from a centre, O, let us draw a horizontal arm to the right, which we will call the v-radius, and another to the left, which we will call the f-radius. Now, then, any quantity x put in the upper or v account, will be so situated that a right-handed, or clock-wise, revolution around O will bring it first to the v-radius; as it will bring a quantity, y, in the f account, to the f-radius; while a left-handed, or counter-clock-wise, turn around O will carry the quantities each to the other radius. This diagram suggests another way of signifying the value of a quantity. Let a heavy line, representing the horizontal bar of the diagram, be drawn under the sign of a quantity, thus, x, to signify that its value is v; and the same bar be drawn above it, thus, ȳ, to signify that its value is f.
259. It may be mentioned that this mode of indicating the value by a bar has a historical appropriateness. For although the two values f and v are, at present, merely distinguished, without any definite difference between them being admitted — and mathematically they do stand upon a precise par, and will continue to do so — yet when dichotomic algebra comes to be applied to logic, it will be found necessary to call one of them verity and the other falsity; and the letters v and f were chosen with a view to that. We shall find it impossible later to prevent this affecting our purest practicable mathematics, in some measure. Now it has been the practice, from antiquity, to draw a heavy line under that whose truth it was desired to emphasize. On the other hand, the obelus, or spit, is already mentioned by Lucian, in the second century A. D., as the sign of denial; and that is why it is frequently even now used in several European countries to denote an n, for non, or the other nasal letter m.
The Greek word {obelos} means a spit, (for example, {pempöbelos} is a five-pronged fork) so that the original notion was that that which is beneath it was transfixed; just as it used to be usual to nail false coins to the counter.
260. There is a small theorem about multitude that it will be convenient to have stated, and the reader will do well to fix it in his memory correctly, with the "each" number as exponent. If each of a set of m objects be connected with some one of a set of n objects, the possible modes of connection of the sets will number nm. Now an assertion concerning the value of a quantity either admits as possible or else excludes each of the values v and f. Thus, v and f form the set of m objects each connected with one only of n objects, admission and exclusion. Hence there are, nm, or 22, or 4, different possible assertions concerning the value of any quantity, x. Namely, one assertion will simply be a form of assertion without meaning, since it admits either value. It is represented by the letter, x. Another assertion will violate the hypothesis of dichotomies by excluding both values. It may be represented by x.
Of the remaining two, one will admit v and exclude f, namely, x; the other will admit f and exclude v, namely x̄.
261. Now, let us consider assertions concerning the values of two quantities, x and y. Here there are two quantities, each of which has one only of two values; so that there are 22, or 4, possible states of things, as shown in this diagram.
Above the line, slanting upward to the right, are placed the cases in which x is v; below it, those in which x is f. Above the line but slanting downward to the right, are placed the cases in which y is v; below it, those in which y is f. Now in each possible assertion each of these states of things is either admitted or excluded; but not both. Thus, m will be 22, while n will be 2; and there will be nm, or 24, or 16, possible assertions. They may be represented by drawing the lines of the diagram between x and y and closing over the compartments for the excluded sets of values. . . . †1
262. Of three quantities, there are 23, or 8, possible sets of values, and consequently 28, or 256, different forms of propositions. Of these, there are only 38 which can fairly be said to be expressible by the signs [used in a logic of two quantities]. It is true that a majority of the others might be expressed by two or more propositions. But we have not, as yet, expressly adopted any sign for the operation of compounding propositions. Besides, a good many propositions concerning three quantities cannot be expressed even so. Such, for example, is the statement which admits the following sets of values:
| x | y | z |
| v | v | v |
| v | f | f |
| f | v | f |
| f | f | v |
Moreover, if we were to introduce signs for expressing [each of] these, of which we should need 8, even allowing the composition of assertions, still 16 more would be needed to express all propositions concerning 4 quantities, 32 for 5, and so on, ad infinitum.
263. The remedy for this state of things lies in simply giving the values v and f to propositions; that is, in admitting them to the universe of quantities. Here I will make an observation, by the way. Although formal logic is nothing but mathematics applied to logic, yet not a few of those who have cultivated it have had distinctly unmathematical minds. Indeed, in man's first steps in mathematics, he always draws back from mathematical conceptions. To first make v represent, let us say, Julius Caesar, and f, Pompey, since they may represent any subjects that are individual and definite, and thereupon further to propose to make every proposition either v or f, shocks the lower order of formal logicians. Such a mind will say, "If we have to distinguish propositions into two categories, let us denote their values by accented, or otherwise modified, letters, say v' and f', and not call them Caesar and Pompey, which is absurd." But I reply that that sort of stickling for usage bars the progress of mathematical thought; that the very fact that it is absurd that a proposition should be Caesar or Pompey proves that there will be no inconvenience, not in calling propositions what you mean by Caesar and Pompey, which, as you say, nobody could mean to do, but in generalizing the conception of Caesar, so as to make it include those propositions which are destined to triumph over the others. To protest against this, is virtually to protest against generalization; and to protest against generalization is to protest against thought; and to protest against thought is a pretty kind of logic. But still the unmathematical mind will ask, why not, however, adopt the v' and f'; for he cannot conquer his shrinking from any generalization that can be evaded. It is the spirit of conservatism, the shrinking from the outré, which is commendable in its proper place; only it is unmathematical: instead of shrinking from generalizations, the part of the mathematician is to go for them eagerly. However, it would not even answer the purpose to distinguish v' and f' from v and f, †P1 for the reason that there would be equal reason for distinguishing propositions about quantities being v or being f from propositions about quantities being v' or being f'; so that we should require a v'' and an f'', and so on, ad infinitum. Now this would hamper us, because we should find we had occasion to form many a proposition about two propositions, as to whether one of the two was v'' or f'', for example, and at the same time whether the other were, say, vIV or fIV, etc. We should, therefore, require still other v's and f's all to no mathematical purpose whatsoever; but, on the contrary, interfering fatally with a very different diversification of v's and f's which, we shall find, really will be needed.
264. If we assign the values v and f to propositions, we must either say that x has the same value as x, in which case x̄ will have the contrary value, and x ≡ x ≡  ≡
≡ 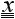 etc., while —(x ≡ x̄), —(x̄ ≡
etc., while —(x ≡ x̄), —(x̄ ≡ 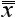 ), so that, x ≡
), so that, x ≡ 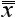 ≡
≡ 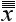 ≡ etc., x̄ ≡
≡ etc., x̄ ≡ 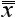 ≡ etc., or else we must say that x̄ has the same value as x, in the which case, x will have the contrary value, so that we shall have x ≡ x̄ ≡
≡ etc., or else we must say that x̄ has the same value as x, in the which case, x will have the contrary value, so that we shall have x ≡ x̄ ≡ 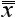 ≡ etc. But x ≡
≡ etc. But x ≡ 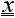 ≡
≡ 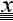 ≡ etc., x ≡
≡ etc., x ≡  ≡ etc. and —(x ≡ x), —(x ≡
≡ etc. and —(x ≡ x), —(x ≡  ), etc. A choice has to be made; and there is no reason for one choice rather than the other, except that I have selected the letters v and f, and the other signs, so as to make the former choice accord with usual conventions about signs.
), etc. A choice has to be made; and there is no reason for one choice rather than the other, except that I have selected the letters v and f, and the other signs, so as to make the former choice accord with usual conventions about signs.
Adopting that former convention, we shall make the value of x the same as that of x. Where it becomes necessary, as it sometimes will, to distinguish them, we may either use the bar, or vinculum, below the line, or we may make use of the admirable invention of Albert Girard, who, in 1629, introduced the practice of enclosing an expression in parentheses to show that it was to be understood as signifying a quantity. †1 For example, x ⥿ y †2 signifies that x is f and y is f. Then (x ⥿ y) ⥿ z, or (x ⥿ y)_ ⥿ z, †3 will signify that z is f, but that the statement that x and y are both f is itself f, that is, is false. Hence, the value of x ⥿ x is the same as that of x̄; and the value of (x ⥿ x)_ ⥿ x †4 is f, because it is necessarily false; while the value of (x ⥿ y)_ ⥿ x ⥿ y †5 is only f in case x ⥿ y is v; and ((x ⥿ x)_ ⥿ x) ⥿ (x ⥿ x ⥿ x) †6 is necessarily true, so that its value is v.
With these two signs, the vinculum (with its equivalents, parentheses, brackets, braces, etc.) and the sign ⥿ , which I will call the ampheck (from {amphékés}, cutting both ways), all assertions as to the values of quantities can be expressed. Thus,
| x is x ⥿ x_ ⥿ x ⥿ x | ||
| x̄ is x ⥿ x | ||
| x:∨:—x is (x ⥿ x ⥿ x) ⥿ (x ⥿ x ⥿ x) | ||
| x·x̄ is (x ⥿ x)_ ⥿ x | ||
| ~(xx̄ yȳ) is {(x ⥿ y)_ ⥿ ((x ⥿ y)_ ⥿ x ⥿ y)} ⥿ {((x ⥿ y)_ ⥿ x ⥿ y) ⥿ x ⥿ y)} | ||
| xx̄ yȳ is (x ⥿ y)_ ⥿ ((x ⥿ y)_ ⥿ x ⥿ y) | ||
| x ≡ y is (x ⥿ y ⥿ y) ⥿ ((x ⥿ x)_ ⥿ y) | ||
| ~(x ≡ y) is (x ⥿ y)_ ⥿ ((x ⥿ x)_ ⥿ y ⥿ y) | ||
| x∨y is (x ⥿ y)_ ⥿ x ⥿ y | ||
| x̄∨ȳ is ((x ⥿ x)_ ⥿ y ⥿ y) ⥿ ((x ⥿ x)_ ⥿ y ⥿ y) [or x~ ⥿ y] | ||
| x̄∨y is ((x ⥿ y)_ ⥿ y) ⥿ (y ⥿ x ⥿ y) [or (y ⥿ x ⥿ x) ⥿ (y ⥿ x ⥿ x)] | ||
| x·y is (x ⥿ x)_ ⥿ y ⥿ y | ||
| x̄·y is x ⥿ x ⥿ y or x ⥿ y ⥿ y | ||
| ⎡ |
x̄·ȳ is x ⥿ y †1 |
⎤ |
265. It is equally possible to express all propositions concerning more than two quantities. Thus, the one between three noticed above †2 is {x ⥿ [y⥿z ⥿ (y⥿y ⥿ z⥿z]} ⥿ {x⥿x ⥿ [(y  z⥿z) ⥿ (y⥿y ⥿ z)]}. That we can equally express every proposition by means of the vinculum [and] one ~ ⥿ is sufficiently shown by the fact that x ⥿ y can be so expressed. †3 It is
z⥿z) ⥿ (y⥿y ⥿ z)]}. That we can equally express every proposition by means of the vinculum [and] one ~ ⥿ is sufficiently shown by the fact that x ⥿ y can be so expressed. †3 It is
(x⥿ ⥿ y⥿y ⥿ (x⥿ ⥿ y⥿y)
266. In order that a sign, say O, should be associative, it is requisite either that whatever quantity x may be, xOx = x, or else, that whatever quantities x and y may be, xOy = yOx and either x = y, or xOx = x, or yOy = y. This may be otherwise stated as follows:
First, Suppose vOv = v and fOf = f. Then I will show that the operation is associative. For if not, it would be possible to give such values to p, q, r, that —{p O(qOr)} ≡ (pOq)Or. But of these three values, p, q, r, some two must be equal. But all three cannot be equal, since then, because of vOv = v and fOf = f, the inequality would not hold. Suppose then first that p ≡ r, p̄ ≡ q. If then pOq ≡ qOp, substituting p for r, pO(qOp) ≡ pO(pOq) ≡ (pOq)Op ≡ (pOq)Or, contrary to the hypothesis. Suppose, secondly, then, that q ≡ r, q̄ ≡ p. Then, substituting q for r, pO(qOq) ≡ pOq; and since this is unequal to (pOq)Oq, it follows that —(p ≡ pOq). But in that case, there being only two different values possible, pOq ≡ q, and pO(qOq) ≡ pOq ≡ q while (pOq)Oq ≡ qOq ≡ q, contrary to the hypothesis. The third supposition, that p ≡ q would evidently lead to an absurdity analogous to the last; so that in no way can the associativeness fail in this case.
Second, Suppose vOv = f and fOf = v. Then I will show that the operation is not associative. For on the one hand,
(vOv)Of ≡ fOf ≡ v;
while, on the other hand, whether vOf = v, so that
vO(vOf) ≡ vOv ≡ f,
or whether vOf = f, so that
vO(vOf) ≡ vOf ≡ f,
in either case, the associative rule is broken.
Third, Suppose vOv = fOf and vOf = fOv. Then I will show that the operation is associative. For otherwise it would be possible to give such values to p, q, r, that
—{pO(qOr)} ≡ (pOq)Or.
But since vOf = fOv, it follows that the second side of the inequality would be equal to
rO(qOp)
so that the inequality requires p̄ ≡ r. But then also —(qOp) ≡ qOr and consequently, the two assumed equations are inconsistent with the inequality, and the operation must be associative.
Fourth, Suppose vOv ≡ fOf, but —(vOf) ≡ fOv. Then I will show that the operation is not associative. For either
(vOv)Ov ≡ fOv, while vO(vOv) ≡ vOf
or (fOf)Of ≡ vOf, while fO(fOf) ≡ fOv;
and in either case since —(vOf) ≡ fOv, the rule of association is violated. The four propositions thus proved, when taken together, are equivalent to the proposition [at the top of page 217]. Of these four, the first shows that ∨, ·, x, †1 y †1 are associative; the third that :∨:—, ≡ , — ≡ , —(:∨:—), are so. The second shows that ⥿, x̄, †1 ȳ, †1 ⥿ , are non-associative; the fourth that ⤙ , ∨—, —(∨—), —( ⤙ ) are so.
267. Another important property of some signs is that a quantity over a vinculum can be interchanged with one beyond the vinculum, so that —
| either | xO(yOz) | and | yO(xOz) |
| or | (xOy)O z | and | (xOz)Oy |
will have the same value. In order that the former formula should hold, it is necessary and sufficient that if xOy, whatever x and y may be, always has the contrary value to that of y when x and y have contrary values, then it should have the contrary value to that of y when x and y have the same value; and conversely, if it has the contrary value to that of y when x and y have the same value, it should also have the contrary value to that of y when x and y have different values. The same rule holds in regard to the second formula interchanging x and y in the statement.
The proposition may be otherwise stated as follows. Let P be the proposition that either vOv = v or fOf = f and Q the proposition that either fOv = v or vOf = f. Then the [first] formula holds if P and Q are both true or both false; but fails if either is true while the other is false.
First, Suppose P and Q both false; so that
| vOv = f, fOf = v, | fOv = f, vOf = v, | |
| Then, | fO(vOv) = fOf = v, | vO(fOv) = vOf = v |
| fO(vOf) = fOv = f, | vO(fOf) = vOv = f, |
and the two formulæ hold.
Second, Suppose the first formula fails. That is,
—{fO(vOv) ≡ vO(fOv)}.
Now if vOv = fOv = v, evidently every expression ending in v would be equal to v, contrary to the hypothesis of the inequality just written. Hence, either vOv = f or fOv = f.
If vOv = f, but fOv = v, the second side of the inequality is vOv = f; so that the first side must be fOf = v, and P is false.
If fOv = f, but vOv = v, the first side of the inequality is fOv = f; so that the second side must be vOf = v, and Q is false.
If vOv = f and fOv = f, the inequality becomes —(fOf) ≡ vOf. Hence, either fOf = v, when P is false or vOf = v, when Q is false; and in any case either P or Q is false.
To suppose that the second of the two formulæ fails, that is, that
—{vO(fOf) ≡ fO(vOf)}
is merely changing f to v and v to f throughout the supposition just examined. Consequently, the result must be obtained by making the same interchange in the result of that supposition. But such interchange will neither change the falsity of P nor that of Q. Consequently, whichever formula fails either P or Q is false; although, by the first supposition, if both are false both formulæ hold. It remains then to examine the cases in which of P and Q one is true and the other false.
Third, Suppose P to be false, and one or other formula to fail. If it be the first that fails, or
—{fO(vOv) ≡ vO(fOv)},
since the first member is fO(vOv) = fOf = v, the second member must be f. This will be the case, if, and only if, either fOv = v or vOf = f; that is, if and only if Q is true. If, however, it be the second formula that fails, or
—{vO(fOf) ≡ fO(vOf)},
again, by interchange of f and v, Q must be true.
Fourth, Suppose Q to be false (that is, fOv = f and vOf = v) and one or other formula to fail. If it be the first, that is, if
—{fO(vOv) ≡ vO(fOv)},
since the second member is vO(fOv) = vOf = v, the first member must equal f and either vOv = v or fOf = f, that is, P will be true. The same results, by interchange of f and v, if the second formula fails.
It follows, then, that if P and Q are both true or both false the formulæ hold, while [if] P and Q differ in respect to truth both formulæ fail, and must be replaced by inequalities.
It will be remarked that one or other of the two formulæ
xO(yOz) ≡ yO(xOz)
(xOy)O z ≡ (xOz)Oy
is true of 14 out of the 16 signs, or all but ⥿ and ⥿ .
Another very commonly true pair of formulæ are
(xOy)Ox ≡ (y O y)Ox
xO(yOx) ≡ xO(y O y).
One formula or the other holds for all the signs except ≡ and — ≡ ; and both hold except for these and x, y, x̄, ȳ.
Somewhat similar to the above are the formulæ
(xOy)Oy ≡ (yOx)Ox
xO(xOy) ≡ yO(yOx).
The first formula holds for :∨:—, ∨, ⤙ , ·, —·, —(:∨:—) and the second for :∨:—, ∨, ∨—, ·, ·—, —(:∨:—).
268. The following table is a key to all the propositions which can be written with one vinculum, at most, and are either necessarily true or necessarily false, whatever be the value of the single letter they contain.
269. A proposition of the form xOx is necessarily true, if O be replaced by any one of the signs in the four corners of the upper quadrant; that is, by :∨:—, ⤙ , ∨—, ≡ , which are, therefore, affirmative signs, according to De Morgan's †1 definition of that word. A proposition of the same form is necessarily false, if O be replaced by any of the former signs in the corners of the lower quadrant; that is, by — ≡ , —·, ·—, —(:∨:—), which are accordingly negative signs. The others are neutral.
Above the horizontal line, there are, outside the large square, four compartments each of which heads a pair of quadrants making half the large square. In each of these compartments is written a formula of the form
x♦(xOx)♥x.
If we strike out the heart and last letter, and replace the diamond by the sign found in its place in any one of those compartments, and replace the O by any one of the eight signs in the half-square that compartment heads, we shall get a proposition necessarily true. Such, for example, are
x ⤙ (x ≡ x)
and
x ∨ (x(⥿ )x).
There will be a similar result if we strike off the first letter and use only the heart; instead of striking off the heart and last letter and using only the diamond. On the other hand, if we enter in either of these ways one of the compartments below the horizontal line, we get a proposition necessarily false. Thus x.~(x.x) is necessarily false. If we replace the diamond by the left-hand, or only, sign [i.e. by ≡ ] in an oval, and the O by any of the signs in the corners of the same square [i.e. by ∨, y, x, .] we have a proposition necessarily true; and so if we replace the heart by the right-hand, or only, letter in an oval [i.e. by — ≡ ]. If instead of replacing the O by one of the four signs in the corners of the same square, we take one of those in the opposite square, we get a proposition necessarily false. If the diamond or heart is replaced by :∨:—, which is in the little square in the middle, and the O by any of the 16 signs in the large square, the proposition will be necessarily true; but if —(:∨:—) replaces the diamond or heart, the proposition will necessarily be false.
270. Of propositions necessarily true of the form
(x♦x)O(x♥x)
there are just eleven hundred. But in 256 of these O is :∨:—, while ♦ and ♥ can be any signs whatever. The remaining 844 are exhibited in the following diagram, not very elegantly, it must be confessed. The sign in the place of the diamond is first to be sought in the first diagram; and its quadrant there is to be denoted by the corresponding cardinal point upon an ordinary map. That is to say, N is either :∨:—, ⤙ , ∨—, ≡ ; E is either ⥿, x̄, ȳ, or ⥿ ; W is either ∨, x, y or .; S is either — ≡ , —., .—, or —(:∨:—). We do the same with the sign in place of the heart. We enter the square on the right hand side below, with the letter for the diamond on the left, and that for the heart at the right. At the intersection of the two rows will be found a spot, from which a line leads to three signs in the left-hand part of the diagram
, or to seven signs in case neither letter is E or W. Any one of these signs being taken as O, the proposition will be necessarily true.271. Rather than inflict upon the reader more of these inconsequential technicalities, I will skip much that systematic thoroughness would require, and will at once notice some propositions necessarily true of the forms:
| (α) (xRy) ♥ [(ySz) ♦ (xOz)] | [(xRy) ♦ (ySz)] ♥ (xOz) (ζ) |
| (β) (xRy) ♥ [(xOz) ♦ (ySz)] | [(xRy) ♦ (xOz)] ♥ (ySz) (ν) |
| (γ) (ySz) ♥ [(xRy) ♦ (xOz)] | [(ySz) ♦ (xRy)] ♥ (xOz) (Θ) |
| (δ) (ySz) ♥ [(xOz) ♦ (xRy)] | [(ySz) ♦ (xOz)] ♥ (xRy) (ι) |
| (ε) (xOz) ♥ [(xRy) ♦ (ySz)] | [(xOz) ♦ (xRy)] ♥ (ySz) (κ) |
| (F) (xOz) ♥ [(ySz) ♦ (xRz)] | [(xOz) ♦ (ySz)] ♥ (xRy) (λ) |
The 24376 formulæ which this table yields are all of this class that it seems worthwhile to give.
272. In order to form a proposition necessarily true of the form (x♦y)O(x♥y), it is only necessary to rewrite it, replacing ♦ and ♥ by the signs they stand for in their most iconic forms, but with :∨:— in place of O. This middle sign is now to be modified as follows:
If there is a quadrant open in both right- and left-hand signs, the top quadrant of the middle one must be left open;
If there is a quadrant open in the left-hand sign alone, the left-hand quadrant of the middle sign must be left open;
If there is a quadrant open in the right-hand sign alone, the right-hand quadrant of the middle sign must remain open;
If there is a quadrant open neither in the right- nor in the left-hand sign, the bottom quadrant of the middle sign must be open.
Any quadrant which is not compelled to be open by this rule, may be closed.
273. The rule may be used inversely, of course. Its principal results are shown in the following table. †1 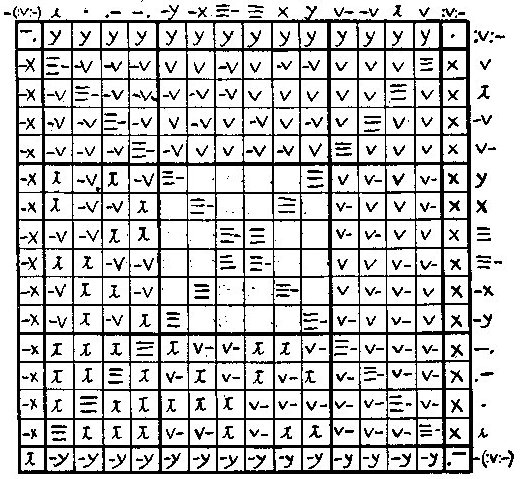
274. From two propositions, one relating to the values of x and y, the other to those of y and z, some proposition concerning the values of x and z can invariably be deduced; although it may be the absurd one, —(x:∨:—z), which is often valuable. In order to ascertain what this is, the value concerning y and z should be written to the left of that concerning x and y, and then lines should be drawn as in this figure.
Whatever quadrants are closed should be shaded, in the one case by vertical shading and in the other by horizontal shading; and this shading should extend over that line which does not pass through the sign concerned. We then read off the conclusion below, noting well that each quadrant consists of two compartments, since the line that does not pass through the sign concerned is disregarded; and unless both are shaded, the quadrant is not closed. For example, given that y∨z̄ and x ≡ ȳ, our diagram becomes as here shown. 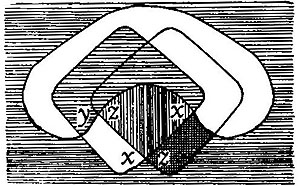
It will be seen that although three quadrants appear, at first glance, to be cut off from the lower sign, yet two of them are not really cut off, since the more remote parts of them are unshaded. The conclusion, therefore, is, that x⥿z.
Such diagrams go by the name of Euler's diagrams, †1 although they are said by Hamilton †2 and by Drobisch †3 to be far older than Euler. The rudimentary idea of them is very likely ancient. But the plan of shading them is due to Mr. Venn. †4 Further on [in book II], I shall show how they may be rendered even more efficient.
So far we have refrained from making use of the obelus, a practice in the style of De Morgan. We shall now see what instant and complete simplification results from the use of it. In the first place, all the signs then become expressible by means of any one of the eight. †5
| ∨ | · | ||||
| ∨— | —∨ | · — | — · | ||
| —∨— | — · — |
275. Dichotomic mathematics, in itself considered, is a trivial thing. Early students of it — in the days of Boole, and later, I mean — may be excused for fancying it could turn out important; I myself long entertained that chimerical dream. The real importance of it lies in the fact that it is a most important aid to the clear understanding of speculative grammar, and even of critical logic; and in the circumstance that, for logical reasons, every mathematical doctrine involves dichotomic mathematics. Where, for example, would be the algebra without a sign of equality? Yet that sign is a dichotomic sign. Were dichotomic algebra only to be used in the study of logic, the simplification of the apparatus would be a secondary consideration; although even then it would be dreary waste of time always to be going back to first principles. But when we reflect that every algebra must involve a dichotomic algebra, we see that such simplification is a serious desideratum. It will be best, therefore, to retain at least two signs of the relations between the values of two quantities. We want these to be as free from necessary formulæ, which will be rules to be borne in mind, as possible; and what rules there are should be as simple as possible. It is, therefore, best to select signs with which it is impossible to construct a formula which is either necessarily true or necessarily false. Moreover, associative signs simplify rules greatly. These two conditions are connected. That is, a sign which satisfies the first necessarily satisfies the second; and the only two signs which do this are ∨ and ·.
276. Suppose, then, we proceed to build the algebra upon these, together with the obelus. We shall then have no need of ⥿ and ⥿, since
x⥿y is x̄∨ȳ and x ⥿ y is x̄·ȳ.
But the very frequently occurring relations x ≡ y and ~(x ≡ y) are still only capable of being expressed in a too complicated way
x ≡ y is x·y ∨x̄·ȳ or x∨ȳ · x̄ ∨y
and
—(x ≡ y) is x̄·y ∨x·ȳ or x∨y · x̄∨ȳ
It will be best to retain one or both of them. Moreover, for logical reasons, the sign ⤙ is of the greatest importance. From a logical point of view, we may say, as we shall see, that it is the most important of any; and even from an algebraical point of view, if we retain ∨ and · as our usual signs, the most important formula of the algebra, apart from those of the commutative and associative principles, requires this sign for its convenient and clear expression. Namely, this formula is
((x∨y)·z) ⤙ (x∨(y·z))
(x·(y∨z)) ⤙ ((x·y)∨z))
expressing a sort of associativeness involving the two signs ∨ and · . . .
277. Adopting these signs, I proceed to state, as definitions, those fundamental conventions from which all the properties of the signs, and all the necessary rules and formulæ of the algebra can be deduced. In doing so, I shall, after Schröder, imitate a practice introduced into geometry, I believe, by Gergonne (about 1820), of writing reciprocally related propositions in parallel columns. The perfect correspondence between aggregation and composition was vaguely asserted by De Morgan, but was first definitely applied to dichotomic algebra and demonstrated, by me. †1
278. Definition of the Quantities of a Dichotomic Algebra.
If x is any quantity of this algebra, then
| No predicate and its negative can both be true of x. That is, x is definite. | Every predicate of its negative must be true of x. that is, x is individual. |
Every proposition concerning quantities of the algebra which is such that it must be true or false but cannot be both is itself a quantity of the algebra; and no other propositions except those which are primarily quantities of the algebra, and those which relate to the values of quantities of the algebra, are quantities of the algebra.
Definitions of v and f
| No quantity of this algebra has, at once, the two values v and f. | Every quantity of this algebra has either the value, v, or the value, f. |
| Every true proposition which is a quantity of this algebra has the value v. | Every false proposition which is a quantity of this algebra has the value, f. |
279. Definitions of the Vinculum and Obelus
| Every quantity written upon a sheet of assertion, is either written | |
| with a vinculum extending under the whole expression, and is thereby asserrted to have the value v. | with an obelus extending over the whole of it, and is thereby asserted to have the value f. |
But such assertions may be in what is equivalent to oratio obliqua, and are not necessarily direct.
280. Definitions of Composition and Aggregation.
If x and y are any quantities of this algebra (whether the same or different)
| If x·y = v, then x = v; | If x y †1 = f, then x = f; y †1 = f, then x = f; |
| If x·y = v, then y = v; | If x y = f, then y = f; y = f, then y = f; |
| If x = v, then if y = v, | If x = f, then if y = f, |
| so likewise x·y = v. | so likewise x y = f. y = f. |
Substantially these definitions of composition and aggregation were given by me in 1880 (Am. Jour. of Math. III, 33). †2 They have the effect of reducing all legitimate transformations to successive legitimate insertions and omissions. The demonstration of this is very easy; but I think it will be more accurately appreciated if I postpone giving it until I have first shown what transformations are, by the above definitions, legitimated through insertions and omissions.
281. I. Any proposition in this algebra, being written on a sheet of assertions, can, without loss of truth, receive the insertion of a vinculum below it.
Demonstration. For, according to the definition of quantities, any proposition of this algebra is a quantity; and by the definition of vinculum and obelus, if written on a sheet of assertions, it must receive either a vinculum or an obelus, either of which being added to it, the result is an assertion concerning the value of the quantity. But this assertion is, by the definition of quantities, itself a quantity. And since this assertion asserts itself to be true, by the definition of v and f, it assigns to itself the value, v. But, by the definition of a vinculum, the assertion that a quantity has the value v is expressed by writing it upon a sheet of assertions with a vinculum below it; and therefore the insertion of the vinculum is legitimated by the assertion of the proposition. For example, if x appears upon the field of assertions we may write x, or if ȳ appears, we may write ȳ. For a transformation is legitimate if it proceeds in accordance with a rule which can never transform a true proposition into a false one.
282. II. A quantity, written on a sheet of assertions with a vinculum under it may, without loss of truth, be transformed by the omission of the vinculum.
Demonstration. Let x be any quantity which is written on the sheet of assertion with a vinculum under it, x. We may confine ourselves to the consideration of the case of the assertion x being true; for if it be not true, it certainly cannot sustain a loss of truth, since, by the definition of quantities, an assertion which has any other than the two grades of truth does not enter into the algebra. Let us first suppose that x is a proposition. Now every asserted proposition virtually asserts its own truth. That is to say, it asserts a fact, which being assumed real, whoever perceives that the proposition asserts that fact, has a perception which can be formulated by saying that what the proposition asserts is true. Therefore, if the vinculum is removed, nothing false is asserted by x, assuming x to be true. The only difference is that x directly asserts what x virtually asserts, and that x implies what x directly asserts. If, on the other hand, x is not an assertion, still its being written upon a sheet of assertions would make it assert itself to be an assertion; and whatever asserts itself to be something asserts something. But, being a quantity of this algebra, unless it is itself primarily an assertion, which would be contrary to our present hypothesis, the only assertion it can be, by the definition of quantities, is that a quantity of the algebra has some value. But the only quantity of the algebra to which x could refer would be itself. It must, therefore, assert that it has itself either the value v or the value f. But, by I, it must assert something which implies the truth of x. Hence, x must assert that its value is v. But this is no more than is asserted by x; and therefore no falsity can be introduced by omitting the vinculum.
283. III. A quantity, written on a sheet of assertion, may, without loss of truth, be transformed by the insertion of two obeli over it.
Demonstration. Let x represent what is written. Being written upon the sheet of assertions, it is an assertion. It, therefore, virtually, at least, consists in the affirmation that some proposition pertinent to the algebra is true, that is, has the value v. Then, since every such proposition is v or f, but not both, it virtually implies that x̄ has the value f. But 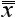 merely asserts that x̄ has the value f. Hence
merely asserts that x̄ has the value f. Hence 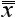 asserts no more than is virtually implied in x, and there will be no loss of truth in inserting the two obeli.
asserts no more than is virtually implied in x, and there will be no loss of truth in inserting the two obeli.
284. IV. If a quantity upon a sheet of assertions has two obeli over it, it may be transformed, without loss of truth, by the omission of the two obeli.
Demonstration. Let 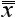 represent what is written. This asserts that x̄ has the value f. That is to say, it asserts that the assertion of x is false. But, then, since x must either have the value v, when x is true, or the value f, when x̄ is true, and since the latter is not the case, it follows that x is true. That is, by II, x can be written on the sheet of assertions. Or, in other words, the two obeli can be omitted, without loss of truth.
represent what is written. This asserts that x̄ has the value f. That is to say, it asserts that the assertion of x is false. But, then, since x must either have the value v, when x is true, or the value f, when x̄ is true, and since the latter is not the case, it follows that x is true. That is, by II, x can be written on the sheet of assertions. Or, in other words, the two obeli can be omitted, without loss of truth.
285. V. If a quantity, were it written by itself on a sheet of assertions, could be transformed, without loss of truth, into another quantity, then were the latter written under an obelus on the field of assertions, it could be transformed without loss of truth into the former under the obelus.
Demonstration. Let x represent the first quantity, y the second, so that it is supposed that if x were written on the sheet of assertions, it could in every case be transformed into y without loss of truth. Suppose, now, that it were not true that ȳ could in every case be transformed into x̄ without loss of truth. Then, there must be some possible case in which ȳ would be true and x̄ not true. To say that x̄ is not true, is expressed by writing 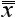 ; so that while ȳ was true, it would be possible for
; so that while ȳ was true, it would be possible for 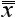 to be true, and hence, by IV, for x to be true. But ȳ is the expression of the assertion that y is f, or y is false. Hence, it would be possible for x to be true but y false; when it would not be true that x would in all cases be transformed into y without loss of truth, which is contrary to the hypothesis. Hence, if x could be transformable into y, without loss of truth, it would be absurd to suppose ȳ not transformable into x̄ without loss of truth.
to be true, and hence, by IV, for x to be true. But ȳ is the expression of the assertion that y is f, or y is false. Hence, it would be possible for x to be true but y false; when it would not be true that x would in all cases be transformed into y without loss of truth, which is contrary to the hypothesis. Hence, if x could be transformable into y, without loss of truth, it would be absurd to suppose ȳ not transformable into x̄ without loss of truth.
286. VI. If a quantity, were it written by itself on a sheet of assertions, could be transformed into another with an obelus over it, then the latter, were it written by itself, without the obelus, could be transformed into the former covered with an obelus.
Demonstration. Let x be the former, y the latter quantity. Then it is assumed that x, were it asserted, could be transformed into ȳ without loss of truth. It follows, then, from V, that 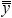 could be transformed into x̄ without loss of truth. But by III, y, were it written on a sheet of assertions, could be transformed into
could be transformed into x̄ without loss of truth. But by III, y, were it written on a sheet of assertions, could be transformed into 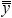 without loss of truth. Therefore, y could be, by the two steps, transformed into x̄ without loss of truth.
without loss of truth. Therefore, y could be, by the two steps, transformed into x̄ without loss of truth.
287. VII. If a quantity, were it written with an obelus over it on a sheet of assertions, could be transformed, obelus and all, into another quantity, without loss of truth, then the latter, were it written with an obelus over it, could be transformed, obelus and all, into the former without its obelus.
Demonstration. Let x be the former, y the latter quantity. Then we assume that x̄ could, in all cases, be transformed into y, without loss of truth; and I am to prove that ȳ could, in all cases, be transformed into x without loss of truth. Since x̄ could be transformed into y, it follows from V that ȳ could be transformed into 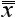 . But by IV,
. But by IV, 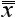 could then be transformed into x; so that ȳ would be transformable into x.
could then be transformed into x; so that ȳ would be transformable into x.
288. VIII. If a quantity, were it written on a sheet of assertions under an obelus, could be transformed, without loss of truth, into another quantity under the same obelus, then, were the latter written without the obelus, it could, without loss of truth, be transformed into the former (without the obelus).
Demonstration. Let x represent the former, y the latter quantity. Then, we assume that x could be transformed into ȳ, without loss of truth; and I am to show that, under that assumption, y could be transformed into x, without loss of truth. By VI, y could be transformed into x, and by IV, 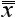 could be transformed into x. Hence, y could be transformed, in two steps, into x.
could be transformed into x. Hence, y could be transformed, in two steps, into x.
289. IX. Any composite which can be written could, were it written on a sheet of assertions, be transformed, without loss of truth, by the omission of any component with its compositor.
Demonstration. A composite can only be written by writing one component after another, singly. It will therefore be sufficient to show that, if the proposition is true for any given composite, it will be true for every composite resulting from the compounding with that composite of an additional component; provided, that I further show the proposition to be true for every composite with the writing of which the writing of any composite begins. For having proved that, I shall have shown that the proposition is true for every composite which can result from the successive affixation of components. For if, notwithstanding this reasoning, a composite could be written of which the proposition were not true, let
a·b·c·d.... ·k·l·m·n
represent such a composite. Now if this composite can be written, it manifestly can be written by first writing a, then affixing ·b, then ·c and so on, that is, by a series of changes each of which consists merely in affixing a new component with its compositor. †P1 But if the proposition is true for the first compound, a·b, so resulting, and none of the steps of the series of operations renders it false for the result of that step, then it never can have been rendered false at all, and must be true for the composite a·b·c·d ····k·l·m·n. Now, if the proposition is false, there must be some single composite for which it is false. It cannot then be false, if I prove that no affixation of a single component can render it false, and if I further prove that it is true at the beginning of writing any composite whatsoever. This general method of proof was invented by the great mathematician Pierre de Fermat †1 (1601-1665).
Let then a·b·c ····k·l·m represent any composite whatever which can be written and of which it is true either that this composite is false, or that the composite which results from it by erasing any component with an adjacent compositor is true. Then I say that, no matter what quantity n may be, it is true of the composite a·b·c····k·l·m·n that either it is false, or every composite which results from erasing from this composite any component with an adjacent compositor is true.
First, then, suppose a·b·c····k·l·m to be false. Then, a·b·c····k·l·m·n must be false. For otherwise, the latter would be true, and consequently have the value v. But in this case, by the first clause of the definition of composition a·b·c····k·l·m would be equal to v, and therefore true and not false, contrary to the hypothesis.
Secondly, consider the alternative, namely that a·b·c····k·l·m, as well as every composite resulting from the omission from a·b·c····k·l·m of a component with its adjacent compositor, is true. Then every such composite will have the value v; and if n likewise has the value v, by the third clause of the definition of composition, every composite resulting from a·b·c····k·l·m·n by the omission of one component will have the value v, and consequently, will be true. But if n has not the value v, then, by the second clause of the definition of composition, the composite a·b·c····k·l·m·n· will not be v, and will therefore not be true, but false.
The simplest form of composite, with which the writing of any other must begin, is that in which there are but two components. By the first and second clauses of the definition of composition, if this is true, that is, equal to v, then each component is equal to v, that is, is true. Therefore, in this case either component can be erased without loss of truth; and the demonstration is thus completed.
290. X. Every quantity written on a sheet of assertions may be transformed without loss of truth, by the insertion of an aggregator with any quantity whatever as aggregant; and if any aggregate which can be written out is written on a sheet of assertions, any additional aggregant, with its aggregator, may be anywhere inserted, without loss of truth.
Demonstration. The demonstration is altogether similar to that of IX. Namely, suppose that a b
b c
c ···
··· k
k l
l m be an aggregate which can be written out, of which this proposition is true; that is to say, that if it be written on a sheet of assertions, that assertion is true, if it be possible to find an aggregant which, being omitted with its adjacent aggregator, the quantity remaining could be written on the sheet of assertions with truth. Then, I say, that the same thing is true, no matter what quantity n may be, of the aggregate a
m be an aggregate which can be written out, of which this proposition is true; that is to say, that if it be written on a sheet of assertions, that assertion is true, if it be possible to find an aggregant which, being omitted with its adjacent aggregator, the quantity remaining could be written on the sheet of assertions with truth. Then, I say, that the same thing is true, no matter what quantity n may be, of the aggregate a b
b c
c ···
··· k
k l
l m
m n; and moreover I aver that the proposition holds of every aggregate with which the writing of an aggregate begins, namely of every aggregate of two aggregants only.
n; and moreover I aver that the proposition holds of every aggregate with which the writing of an aggregate begins, namely of every aggregate of two aggregants only.
For assume that the proposition is true of a b
b c
c ···
··· k
k l
l m; that is to say, that either this is true or the quantity which results from the omission from it of any aggregant with an adjacent aggregator is false. Then, I say, of the aggregate a
m; that is to say, that either this is true or the quantity which results from the omission from it of any aggregant with an adjacent aggregator is false. Then, I say, of the aggregate a b
b c
c ···
··· k
k l
l m
m n, that it either is true, or else that no matter what single aggregant of it with an adjacent aggregator be omitted, the resulting quantity, being written on a sheet of assertions, makes a false assertion. Consider, in the first place, the case in which a
n, that it either is true, or else that no matter what single aggregant of it with an adjacent aggregator be omitted, the resulting quantity, being written on a sheet of assertions, makes a false assertion. Consider, in the first place, the case in which a b
b c
c ···
··· k
k l
l m is true, that is equals v. Then it does not equal f and consequently, by the first clause of the definition of aggregation, a
m is true, that is equals v. Then it does not equal f and consequently, by the first clause of the definition of aggregation, a b
b c
c ···
··· k
k l
l m
m n cannot equal f, but must equal v, that is, must be true.
n cannot equal f, but must equal v, that is, must be true.
Consider next the other alternative, that both a b
b c
c ···
··· k
k l
l m and also every quantity resulting from the omission from it of an aggregant and an adjacent aggregator are false. Then, these are all equal to f and if, besides, n is equal to f, by the third clause of the definition of aggregation, every quantity which results from the omission from a
m and also every quantity resulting from the omission from it of an aggregant and an adjacent aggregator are false. Then, these are all equal to f and if, besides, n is equal to f, by the third clause of the definition of aggregation, every quantity which results from the omission from a b
b c
c ···
··· k
k l
l m
m n is also equal to f, is therefore false. If, however, n is not equal to f, then by the second clause of the definition of aggregation a
n is also equal to f, is therefore false. If, however, n is not equal to f, then by the second clause of the definition of aggregation a b
b c
c ···
··· k
k l
l m
m n is not equal to f, and must be equal to v and hence, when written on a sheet of assertions, must be true.
n is not equal to f, and must be equal to v and hence, when written on a sheet of assertions, must be true.
But if an aggregate has two aggregants only, then, by the first and second clauses of the definition of aggregation, if either of those aggregants is true, and so equal to v, and not to f, then the aggregate cannot have the value f, but must have the value v, and when written on a sheet of assertions must constitute a true assertion.
Corollary. It follows that every composite is true or equal to v only in case all its components are so; being false, or equal to f, if any one of its components is so; while an aggregate is true, or equal to v, if any one of its aggregants is so, and is only false, or equal to f, if all its aggregants are so. But this applies only to composites and aggregants which can be written out.
291. XI. If every one of the components of a composite might, with truth, be written upon a sheet of assertions, the composite itself can be so written, if it can be written out.
Demonstration. I shall use the Fermatian method. Assume that it is true of the composite (which can be written out) a·b·c ···· ·k·l·m. Then it is also true of the composite a·b·c ··· ·k·l·m·n, by the third clause of the definition of composition. It is true of every composite of two components by the same clause. Hence it is always true.
292. XII. If an aggregate might, with truth, be written out upon a sheet of assertions, then some one of its aggregants might be so written.
Demonstration. Let a b
b c
c ··
··  k
k l
l m be an aggregate of which it is true either that it cannot be written with truth upon a sheet of assertions or that some aggregant of it might be so written (although we may not know which one). Then the same will be true of the aggregate a
m be an aggregate of which it is true either that it cannot be written with truth upon a sheet of assertions or that some aggregant of it might be so written (although we may not know which one). Then the same will be true of the aggregate a b
b c
c ···
··· k
k l
l m
m n. For consider, first, the alternative that a
n. For consider, first, the alternative that a b
b c
c ···
···  k
k l
l m cannot be asserted with truth. Then its value is not v but f. If then n is likewise f, it follows from the third clause of the definition of aggregation that a
m cannot be asserted with truth. Then its value is not v but f. If then n is likewise f, it follows from the third clause of the definition of aggregation that a b
b c
c ···
···  k
k l
l m
m n is f and so could not be asserted with truth. But if n is not f, then this is an aggregant of a
n is f and so could not be asserted with truth. But if n is not f, then this is an aggregant of a b
b c
c ··
··  k
k l
l m
m n which can be asserted with truth. The other alternative is that some aggregant of a
n which can be asserted with truth. The other alternative is that some aggregant of a b
b c
c ···
···  k
k l
l m can be asserted with truth. But that aggregant will equally be an aggregant of a
m can be asserted with truth. But that aggregant will equally be an aggregant of a b
b c
c ·· k
·· k l
l m
m n. Finally, if there are but two aggregants, the proposition is true by the third clause of the definition of aggregation.
n. Finally, if there are but two aggregants, the proposition is true by the third clause of the definition of aggregation.
293. XIII. As long as the only signs used are those described, any quantity which, if written alone on a sheet of assertions, could be transformed into a certain other, without loss of truth, can be so transformed wherever it occurs as a part of a directly asserted quantity, so long as it is not under an obelus.
Demonstration. Let x be a quantity which, if asserted to have the value v, could be replaced by y without loss of truth.
Then, in the first place, if x is a component of a directly asserted composite, it can be replaced by y without loss of truth. For if any of the other components is equal to f, and so is false, by IX, the composite is not true, and is therefore not capable of sustaining a loss of truth. But if every other component is equal to v, and this component is also v, then by XI, the composite is likewise v; while if this component is f, by X, the composite is f. Thus, the value of the whole is the same as that of this component x; and if this component is transformed into y, which is necessarily v if x is v, the whole composite remains v.
Next, suppose that that x is an aggregant of the asserted quantity. Then, if any of the other aggregants is v, the aggregate will be v, whatever transformation x may undergo. But if all the others are f, and x is f, the aggregate, will, by XII, be f, while if x is v, by X, the aggregate will be v. Thus the value of the whole aggregate will be the same as that of x; and if x is replaced by y, which is necessarily v if x is v, the value of the aggregate will remain v.
Thus the transformations of an aggregant, as well as those of a component, follow the same rules as those of an entire asserted quantity; and consequently, if x be an aggregant of a component, or a component of an aggregant, or be in any other relation to the asserted quantity describable by the alternate use of component and aggregate, as it must be if we use no other signs than those described, and if x is not under an obelus, then it is subject to the same rules of transformation as if it were asserted alone.
294. XIV. As long as the only signs used are those described, any quantity into which another could be transformed without loss of truth, if the latter were asserted alone, can, if it occurs anywhere under a single obelus in a directly asserted quantity, be there transformed into that latter.
Demonstration. Let x and y represent the two quantities, so that in the assertion that x has the value v, x could be replaced by y, without loss of truth. Then, I say that if, in a directly asserted quantity, y occurs anywhere under a single obelus, it can be transformed into x without loss of truth. For let Y be the entire expression which is under the same obelus as y; and let X be what Y would become if y were replaced by x. Then, by XIII, if X were asserted, it could be transformed into Y. And consequently, by V, Y̅, if it were asserted alone could be transformed into X̅. Hence, by XIII, situated as Y̅ is, not under any obelus, it can be transformed into X̅. But this transformation consists only in replacing y by x under a single obelus.
295. Definition. Let us say that two operations are internal negatives of one another, if and only if, either gives a result of contrary value to the result of the other when whatever quantities it operates upon are of contrary value to those operated upon by that other; and let us write an obelus over a sign of the combination of two quantities to signify the internal negative of that sign.
Then we shall have the following pairs of internal negatives
| :∨:— | and | —(:∨:—) |
 or ∨ or ∨ |
and | · |
| ⥿ | and | ⥿ |
| ⤙ | and | —· |
| ∨— | and | ·— |
| ≡ | and | —( ≡ ) |
| x | and | x̄ |
| y | and | ȳ |
The obelus and vinculum will each be its own internal negative.
Since a quantity operates upon nothing, its internal and negative will be its own negative; that is x and x̄, v and f will be internal negatives of each other.
296. XV. Every expression of a quantity has the contrary value to the expression which results from the substitution in it of the internal negative of each quantity and operation.
Demonstration. For, in the first place, this is true regarding single letters. For let x represent any single letter. Then, since x operates upon nothing, x̄ gives the contrary value to x when it operates upon whatever x operates upon. In the second place, it is true of expressions operated upon by the vinculum and obelus. For since x has the contrary value to x̄, the vinculum is its own internal negative; and since x̄ has the contrary value to 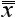 , the obelus is its own internal negative. In the next place, the proposition is true of any operator upon two operands; for, by the definition, xOy has the contrary value to that of x̄O̅ȳ. Hence, if y is u♦v, xO(u♦v) has the contrary value to x̄O̅(ū♦v). And so if y = w̅, xOw̅ has the contrary value to x̄O̅w. And by Fermatian reasoning, it is evident that this will be so in every case.
, the obelus is its own internal negative. In the next place, the proposition is true of any operator upon two operands; for, by the definition, xOy has the contrary value to that of x̄O̅ȳ. Hence, if y is u♦v, xO(u♦v) has the contrary value to x̄O̅(ū♦v). And so if y = w̅, xOw̅ has the contrary value to x̄O̅w. And by Fermatian reasoning, it is evident that this will be so in every case.
297. XVI. Every necessarily true proposition concerning the values, or relations between the values, of quantities of dichotomic algebra will remain necessarily true after it has been modified by everywhere interchanging f and v, and internal negatives of operators upon two letters, and when categorical affirmation and denial, protasis and apodosis of the same conditional sentence, copulation and disjunction are likewise interchanged.
Demonstration. I have to prove that if a certain form of algebraic expression is necessarily true, then if that form is modified by the interchange of f and v, of · and  , of ≡ and —( ≡ ), of ⤙ and —·, etc., it becomes necessarily false; and further it being necessarily true, that from the truth of one expression the truth of another follows, it will be equally true that from the truth of the latter, modified as above, the truth of the former, modified in the same way, equally follows by necessity. Finally, I have to show that to say that if any quantity, A, is v, then both the quantities B and C are v, is the same as to say that if either B̅' or C̅' is v, then A̅' is v; where, A̅', B̅', C̅' are the above-described modifications of A, B, C.
, of ≡ and —( ≡ ), of ⤙ and —·, etc., it becomes necessarily false; and further it being necessarily true, that from the truth of one expression the truth of another follows, it will be equally true that from the truth of the latter, modified as above, the truth of the former, modified in the same way, equally follows by necessity. Finally, I have to show that to say that if any quantity, A, is v, then both the quantities B and C are v, is the same as to say that if either B̅' or C̅' is v, then A̅' is v; where, A̅', B̅', C̅' are the above-described modifications of A, B, C.
I first remark that to call a proposition concerning the values, or relations between the values, of quantities of dichotomic algebra necessarily true is to say that it is true whatever be the values of the quantities to which it relates. If, then, a proposition is necessarily true, it remains so when for all the single ordinary letters (not v and f) that are mentioned in its statement, the negatives of these letters are substituted. But if this substitution be made, and the internal negative of each combination be then substituted for the combinations themselves, the result will be the same modification which is described in the enunciation of this theorem. For the single letters will be restored to their original conditions with respect to having obeli over them, but f and v will be interchanged; the vincula and obeli will remain unchanged; and the signs of operations upon two quantities will be changed into their internal negatives. The quantities described by the combinations so modified will thus have values contrary to the values of the corresponding unmodified combinations, after the obeli are applied to the single letters. Consequently, if we make the proper changes in what is said of them, the initial proposition which was necessarily true will remain necessarily true of these so modified combinations. In particular, if the original proposition represents the assertion that a combination, C, is necessarily true, or has the value v; and if C' is the modification produced by putting obeli over the single letters of C, then that C' is necessarily true, or has the value v, will be equally true; and consequently, that C̅' is necessarily false will be equally true; where C' will be the modification of C described in the enunciation. So if the necessarily true proposition is that if a certain combination, A, is true, then a certain combination, B, is true, it remains equally necessary that if A' is true B' is true; and consequently, equally true that if B̅' is true (and therefore B' is not true) then A̅' will be true (i.e., A' will not be true). So, if the original proposition be that if A is true, then both B and C are true, and [if] this be necessarily true, it is equally necessary that if A' is true, then both B' and C' are true, and consequently, [it] is equally necessary that if either B̅' or C̅' be true (so that either B' or C' is false), then A̅' is true (or, A' is false). The necessary truth of the proposition is thus made plain.
298. XVII. If a quantity have the value v, then this quantity may be inserted as a component of the whole or any part of an asserted quantity, and any component of a part (or the whole) of an asserted quantity, can be repeated, without loss of truth, as a component of this part or of any part of it.
Demonstration. By the first clause of the definition of composition if a·v has the value v, so has a; and by the third clause of the same definition, if a has the value v, so has a·v. Thus a and a·v have in all cases the same value, and the substitution of the latter for the former in any part of an expression must be without effect upon the value of it, since the value of an expression of a given form depends exclusively on the values of its parts.
Consequently, if a has the value v, its introduction anywhere as a component cannot change the value of the expression into which it is introduced; but if a has the value f, and is a component, the composite has in any case the value f, whatever be done to the other components. Thus, its introduction, as a component of a part of the composite of which it is a component, can never alter the value.
Corollary. It follows, by XVI, that a quantity having the value f may be introduced as an aggregant into any part of an assertion; and further, that any quantity, repeated as an aggregate of any part of any part of an assertion of which it is an aggregant, may be omitted in that inner repetition.
Corollary. We may place here the propositions that composition and aggregation are commutative and associative.
Given a·b, we can, by insertion, write b·a·b, for if a·b is v, so is b, and if b and a·b are v, so is b·a·b. But then, by omission, we get b·a. For if b·a·b is v, so is a·b, and if a·b is v, so is a. Also, if b·a·b is v, so is b; and if both b and a are v, so is b·a.
Again, given (a·b)·c, we get by insertion (a·b·c)·c. For if (a·b)·c is v, so is c; and if c is v, b·c is v, if b is v; and if a·b·c is v if a·b is v, and if (a·b)·c is v, so is (a·b·c)·c. But then by omission we get a·b·c.
Since composition has these properties, so, by XVI has aggregation.
299. XVIII. The negative of a component may be introduced into any part of its composite as an aggregant, without loss of truth.
Demonstration. For if a has the value v, its negative is f, and as an aggregant can affect the value of nothing. But if a has the value f, being a component, the composite is f, no matter how the other components be transformed.
Corollary. It follows that if the negative of an aggregant occurs in any part of the aggregate as a component, it may be omitted.
300. XIX. A quantity which is a component of every aggregant of an aggregate may be introduced as a component of the whole, without altering the value; and it may then be omitted from the aggregants, without altering the value.
Demonstration. I have to prove that a·x b·x
b·x c·x
c·x etc. has the same value as (a·x
etc. has the same value as (a·x b·x
b·x c·x
c·x etc.)·x, and also the same value as (a
etc.)·x, and also the same value as (a b
b c
c etc.)·x.
etc.)·x.
First, suppose that the value of a·x b·x
b·x c·x
c·x etc. is v. Then, by the third clause of the definition of composition, the value of (a·x
etc. is v. Then, by the third clause of the definition of composition, the value of (a·x b·x
b·x c·x
c·x etc.)·(a·x
etc.)·(a·x b·x
b·x c·x
c·x etc.) will also be v.
etc.) will also be v.
But, then, omitting components, (a·x b·x
b·x c·x
c·x etc.)·(x
etc.)·(x x
x x
x etc.) will also be v. But, then, (a·x
etc.) will also be v. But, then, (a·x b·x
b·x c·x
c·x etc.)·x will be v. For if (a·x
etc.)·x will be v. For if (a·x b·x
b·x c·x
c·x etc.)·(a·x
etc.)·(a·x b·x
b·x c·x
c·x etc.) is v, then by the second clause of the definition of composition, a·x
etc.) is v, then by the second clause of the definition of composition, a·x b·x
b·x c·x
c·x etc. is v; and then by the third clause of the definition of aggregation, either a·x or b·x or c·x etc. is v; and then, by the second clause of the definition of composition, x is v; and then, since by the first clause of the definition of composition, (a·x
etc. is v; and then by the third clause of the definition of aggregation, either a·x or b·x or c·x etc. is v; and then, by the second clause of the definition of composition, x is v; and then, since by the first clause of the definition of composition, (a·x b·x
b·x c·x
c·x etc.)·(a·x
etc.)·(a·x b·x
b·x c·x
c·x etc.) is v, a·x
etc.) is v, a·x b·x
b·x c·x
c·x etc. is v, it follows from the third clause of the same definition that (a·x
etc. is v, it follows from the third clause of the same definition that (a·x b·x
b·x c·x
c·x etc.)·x is v. And further, if (a·x
etc.)·x is v. And further, if (a·x b·x
b·x c·x
c·x etc.)·x is v, it follows, by omission of components that (a
etc.)·x is v, it follows, by omission of components that (a b
b c
c etc.)·x is v.
etc.)·x is v.
Secondly, suppose that (a·x b·x
b·x c·x
c·x etc.) is f. Then, by the first clause of the definition of composition, (a·x
etc.) is f. Then, by the first clause of the definition of composition, (a·x b·x
b·x c·x
c·x etc.)·x is f. And further, a·x and b·x and c·x etc. have by the first and second clauses of the definition of aggregation, all severally the value f. Then, if x is v, by the third clause of the definition of composition, a, b, c, etc. have all severally the value f, and by the third clause of the definition of aggregation, a
etc.)·x is f. And further, a·x and b·x and c·x etc. have by the first and second clauses of the definition of aggregation, all severally the value f. Then, if x is v, by the third clause of the definition of composition, a, b, c, etc. have all severally the value f, and by the third clause of the definition of aggregation, a b
b c
c etc. has the value f; and by the first clause of the definition of composition (a
etc. has the value f; and by the first clause of the definition of composition (a b
b c
c etc.)·x has the value f. Suppose, on the other hand, that x has the value f. Then, by the second clause of the definition of composition (a
etc.)·x has the value f. Suppose, on the other hand, that x has the value f. Then, by the second clause of the definition of composition (a b
b c
c etc.)·x has the value f.
etc.)·x has the value f.
Thus, in every case, a·x b·x
b·x c·x
c·x etc. and (a·x
etc. and (a·x b·x
b·x c·x
c·x etc.)·x and (a
etc.)·x and (a b
b c
c etc.)·x have the same value.
etc.)·x have the same value.
Corollary. It follows that
(aΨx)·(bΨx)·(cΨx) etc.
=(aΨx)·(bΨx)·(cΨx)· etc. Ψx
When we come to the algebra of logic, there will be a highly important remark to make concerning this theorem.
301. The above are, I believe, all the theorems of dichotomic algebra with which it is worthwhile to trouble the reader. There are, however, a few problems to be considered. Of these, I shall give those methods of solution which seem to me to be upon the whole the most useful, taking into consideration something besides their brevity in very complicated cases — making this, indeed, decidedly a secondary consideration, in view of the excessive rarity of cases in which the reader will ever have occasion to apply the algebra to complicated problems, and in view of the very moderate degree of mathematical ingenuity requisite to clearing away the complexity even from these few. What seems to me desirable is that the procedure should have that kind of simplicity which makes it easy to remember or to reconstruct if its details are forgotten.
The first problem is to put an expression into such a form that a certain letter appears only as an aggregant of a component, or as the negative of an aggregant of a component. I first gave a general solution of this problem which I do not think can be improved upon. †1 Let x be the letter in question; and let the expression be Fx. Then,
I must say that there was little originality in this solution, since it was but the reciprocal of a proposition of Boole's. If it is desired to separate two letters in this way, we have
The procedure for a greater number of letters will be similar. But it is never really necessary to separate more than one.
The proof is simple enough. If Fx has the value v, either x has the value v, when Fx becomes Fv or x̄ has the value v, so that, in any case, Fv x̄ has the value v; and further, either x̄ has the value v, when Fx becomes Ff or x has the value v, so that, in any case, Ff
x̄ has the value v; and further, either x̄ has the value v, when Fx becomes Ff or x has the value v, so that, in any case, Ff x has the value v. Consequently, if Fx has the value v, the composite (Fv
x has the value v. Consequently, if Fx has the value v, the composite (Fv x̄)·(Ff
x̄)·(Ff x) has the same value. But if Fx has the value f, either x has the value v, when Fx becomes Fv, and Fv
x) has the same value. But if Fx has the value f, either x has the value v, when Fx becomes Fv, and Fv x̄ has the value f, or x has the value f, when Fx becomes Ff, and Ff
x̄ has the value f, or x has the value f, when Fx becomes Ff, and Ff x has the value f. Thus, if Fx has the value f, one or other of the components of (Fv·x)·(Ff
x has the value f. Thus, if Fx has the value f, one or other of the components of (Fv·x)·(Ff x) has the value f, and again (Fv
x) has the value f, and again (Fv x̄)·(Ff
x̄)·(Ff x) has the same value as Fx.
x) has the same value as Fx.
Boole's reciprocal problem is to put an expression into a form in which a given letter or its negative appears only as a component of an aggregant. The solution is
We now have to take a step which I first took in my memoir dated, 1870 Jan. 26. †P1 Let us start from the sixteen assertions concerning the values of two dichotomic quantities, and take the signs of the operations they involve in a new sense, which may be distinguished by a dot over these signs, regarding these operations themselves as quantities, and at the same time operators upon the second of the two quantities, thereby producing the first. Then, the four :, · ∸, ∸., · ⥿ , will by aggregation give all the rest, except —(:∨:—). Thus,
302. Now mathematicians have long ago agreed upon generalizing the meaning of the word 'multiplication' so as to make it signify the operation of applying, as multiplier, an operation to the result of another operation, which last operation is regarded as the multiplicand. I identify this operational multiplication, which is commonly called functional multiplication, with my relative multiplication, which is the operation of so combining a relative term — such as 'lover of' — as multiplier, with a correlate as multiplicand, so as to yield, as product, the relate which is in the relation signified by the relative term to the object indicated as correlate. A mathematical operator is nothing but a mathematical relative term. Then, the relative, or functional, multiplication table of :, · ∸ , ∸·., · 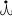 will be as here shown.
will be as here shown.
303. My father afterward, but independently, obtained two multiplication tables of similar form in his Linear Associative Algebra (1st Ed., pp. 30, 59; 2nd Ed. [American Journal of Mathematics, 1881], edited by me, pp. 111, 132), which I showed †1 was due to their being, in essence, the same thing. He further discovered that by means of ordinary imaginary algebra, quaternions, or rather Hamilton's biquaternions, can be put into this form. †2 Namely, if we put
(· ∸ +∸ ·)√-1 = j
(· ∸ - ∸ ·) = k
we get the multiplication table of quarternions, which is as here shown.
304. This is only interesting here as showing how dichotomic mathematics may influence higher orders of mathematics. But quaternions proper does not admit of imaginary coefficients; and biquaternions is essentially a different thing. Quaternions is a quaternary, or tetrachotomic, algebra of which [I gave] the proper representation in February, 1882. †1
305. If the operations are to be considered as quantities, what we have considered, and what are, the quantities of dichotomic algebra, sink to the rank of umbræ, or ingredients of quantities. It was Leibniz †2 who in 1693, April 28, first introduced into algebra this conception of ingredients of quantities; and unfortunately, he neglected to provide a suitable name for them. It so happened that it was not until three half centuries later, when they had been used by a hundred writers, at the very least, and had figured in familiar textbooks, that the seething brain of Sylvester allowed him to claim them as his own invention, and to bestow upon them the name of umbræ. †3 The name could not well be more inappropriate; for whoever heard of shadows conspiring to create a substance? Besides, there is nothing to prevent umbræ being identified with ordinary quantities — or rather all ordinary quantities being identified with some umbræ: such a step is, often, a most useful mathematical generalization. An umbra, or better, an ingredient of a quantity, is a logical symbol, a set of which systematically, and from a logical point of view, describes a quantity, without any necessary reference to its value. For example, if the velocities of two couriers are denoted respectively by u1 and u2, then u, 1, and 2, are umbræ, or ingredients, of the quantities u1, and u2. The first example given by Leibniz was of three general simultaneous linear equations between two quantities, which he wrote thus:
10+11x+12y = 0
20+21x+22y = 0
30+31x+32y = 0
Here the numbers have nothing to do with the values of the coefficients, which may be anything. The first figure shows simply what equation is referred to and the second what term of that equation. My particular umbral notion of 1870 †1 for relative terms, which has been generally approved, was A:B, where A and B are individual objects, and A:B is that operation upon B which produces A, but operating upon any other individual than B produces f, even if that other individual have the same value as B. Nevertheless, since values, in all sorts of algebra, are singular and definite objects, to which the principles of contradiction and excluded middle apply, there is nothing to prevent our taking the colon in a special sense, so that A:B shall operate, not upon B logically considered, but upon the value of B, giving the value of A. It is in this sense that we may write
| : = v:v | 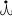 = f : f = f : f |
| · ∸ = v:f | ∸· = f : v.... |
306. If we identify v with ẋ, and f with x̄̇, the distinction between relative multiplication and composition will disappear in regard to the ordinary quantities of dichotomic algebra. For just as
v·v = v so ẋ:ẋ = ẋ †2 v·f = f ẋ:x̄̇ = x̄̇ f·v = f x̄̇:ẋ = x̄̇ f·f = f x̄̇:x̄̇ = x̄̇
But in regard to these new quantities, the distinction will be maintained. For example,
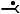 : †2
: †2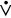 — = ·
— = · 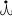 . (
. ( ·
· —) = (
—) = ( ) = (
) = ( —·
—·  ).
).  —: †2 ⤙ =·.
—: †2 ⤙ =·.
I shall not further enlarge upon this matter at this point, although the conception mentioned opens a wide field; because it cannot be set in its proper light without overstepping the limits of dichotomic mathematics.
§4. Trichotomic MathematicsP
307. We have already, along one line, traversed the marches between dichotomic and trichotomic mathematics; for the general idea of operational multiplication is as purely triadic as it could well be, involving no ideas but those of the triad, operator, operand, and result. Relative multiplication, however, involves a marked dichotomic element since (A:B):(C:D) is one of the two, f or A:D, according as (B:C) is one of the two f or v.
308. Trichotomic mathematics is not quite so fundamentally important as the dichotomic branch; but the need of a study of it is much greater, its applications being most vital and its difficulties greater than the dichotomic. Nevertheless, it has received hardly any direct attention. The permutations of three letters have, of course, been noticed, along with other permutations. The theory of the cubic equation is fully made out; along with those of plane and twisted cubic curves. There is also an algebra of novenions. In addition, considerable studies have been made in a particular province of trichotomic mathematics by logicians, without their recognizing the triadic character of the subject.
A trichotomic mathematics entirely free from any dichotomic element appears to be impossible. For how is the mathematician to take a step without recognizing the duality of truth and falsehood? Hegel and others have dreamed of such a thing; but it cannot be. Trichotomic mathematics will therefore be a 2X3 affair, at simplest.
309. I will begin this topic by a glance at some of the logico-mathematical generalities, without being too scrupulous about excluding higher numbers than three.
The most fundamental fact about the number three is its generative potency. †1 This is a great philosophical truth having its origin and rationale in mathematics. It will be convenient to begin with a little a priori chemistry. †2 An atom of helion, neon, argon, xenon, crypton, appears to be a medad (if I may be allowed to form a patronymic from {méden}). Argon gives us, with its zero valency, the one single type
A.
Supposing H, L, Na, Ag, etc. and F, Cl, Br, I to have strictly unit valency (which appears not to be true; at least, not for the halogens), then they afford only the two types
H-H H-F,
if these can be called two.
Assuming G (glucinum), etc. with O, S, etc., to have valency 2 (certainly not true), they might give an endless series of saturated rings, by themselves.
and so on, ad infinitum. With the monads, these dyads would give terminated lines.
H-O-H H-O-O-H Cl-O-O-O-H.
and so on, ad infinitum. But they can give no other types than single rings and terminated lines.
Triads, on the other hand, will give every possible variety of type. Thus, we may imagine the atom of argon to be really formed of four triads, thus
We may imagine the monadic atom to be composed of seven triads; thus;
A dyad will be obtained by breaking any bond of A; while higher valencies may be produced, either simply
or in an intricate manner.
One atom forms one type without a ring  , one with a one-atom ring
, one with a one-atom ring  : two in all.
: two in all.
Two atoms form, in one piece, one acyclic type  , one with one protocycle
, one with one protocycle  , one diprotocyclic type
, one diprotocyclic type  , one monodeuterocyclic
, one monodeuterocyclic 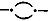 , one dideuterocyclic type
, one dideuterocyclic type  : five in all.
: five in all.
Three atoms form one acyclic type  , one monoprotocyclic
, one monoprotocyclic  , one diprotocyclic
, one diprotocyclic  , one monodeuterocyclic
, one monodeuterocyclic  , one protodeuterocyclic
, one protodeuterocyclic  , one tritocyclic
, one tritocyclic  one deuterotritocyclic
one deuterotritocyclic  : seven in all.
: seven in all.
Four atoms form two acyclic types 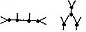 , two monoprotocyclic
, two monoprotocyclic 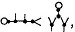 , two diprotocyclic
, two diprotocyclic  one triprotocyclic
one triprotocyclic  two monodeuterocyclic
two monodeuterocyclic 
 , one dideuterocyclic
, one dideuterocyclic  , two monodeuteromonoprotocyclic
, two monodeuteromonoprotocyclic  , one monodeuterodiprotocyclic
, one monodeuterodiprotocyclic  , one monotritocyclic
, one monotritocyclic  , one ditritocyclic
, one ditritocyclic  (where there is, of course, also a four-atom ring), one tritritocyclic
(where there is, of course, also a four-atom ring), one tritritocyclic  (so I name it, although there are four three-atom rings and three four-atom rings), one prototritocyclic
(so I name it, although there are four three-atom rings and three four-atom rings), one prototritocyclic  , one deuterotritocyclic
, one deuterotritocyclic  , one protodeuterotritocyclic
, one protodeuterotritocyclic  ; one tettartocyclic
; one tettartocyclic  , one monodeutero-tettartocyclic
, one monodeutero-tettartocyclic  , one dideuterotettartocyclic
, one dideuterotettartocyclic  , one tritotettartocyclic
, one tritotettartocyclic  : twenty-three in all, if I have repeated none. With larger numbers of atoms the types multiply astonishingly.
: twenty-three in all, if I have repeated none. With larger numbers of atoms the types multiply astonishingly.
310. It would scarcely be an exaggeration to say that the whole of mathematics is enwrapped in these trichotomic graphs; and they will be found extremely pertinent to logic. So prolific is the triad in forms that one may easily conceive that all the variety and multiplicity of the universe springs from it, though each of the thousand corpuscles of which an atom of hydrogen consists be as multiple as all the telescopic heavens, and though all our heavens be but such a corpuscle which goes with a thousand others to make an atom of hydrogen of a single molecule of a single cell of a being gazing through a telescope at a heaven as stupendous to him as ours to us. All that springs from the
— an emblem of fertility in comparison with which the holy phallus of religion's youth is a poor stick indeed.
311. Let us now glance at the permutations of three things. To say that there are six permutations of three things is the same as to say the two sets of three things may correspond, one to one in six ways. The ways are here shown
No one of these has any properties different from those of any other. They are like two ideal rain drops, distinct but not different. Leibniz's "principle of indiscernibles" is all nonsense. No doubt, all things differ; but there is no logical necessity for it. To say there is, is a logical error going to the root of metaphysics; but it was an odd hodge-podge, Leibniz's metaphysics, containing a little to suit every taste. These arrangements are just like so many dots, as long as they are considered in themselves. There is nothing that is true of one that is not equally true of any other — so long as in the proposition no other is definitely mentioned. But when we come to speak of them in pairs, we find that pairs of permutations differ greatly. To show this let us make a table like that which we formed in dichotomic algebra. On one side we enter the table with r, s or t, on the other with [o, p, or q], and at the intersections of the rows we find the figure of the permutation in which the two correspond. In order to avoid putting two symbols in one square I repeat the table. We have then
It will be seen that from this point of view, that of their relations to one another, the permutations separate themselves into two sets. In any one set, there are no two permutations which make the same letter correspond to the same letter; while of pairs of permutations of opposite sets, each agrees in respect to the correspondence of one letter.Since there are six permutations, there could be 26, or sixty-four different assertions which might be made concerning an unknown two, as to what ones of the six they were. But from these sixty-four, it will be interesting to select a set of six, such that any one, being relatively multiplied by any other, the product is one of the six, and such that the product is different from what it would be if either multiplier or multiplicand were alone different. Not that this is to be true of all quantities of the algebra, but only of the six single letters. For the larger condition would render the problem impossible. Let the six letters conforming to this condition be i, j, k, l, m, n. Since every product of these letters is to be one of the letters, and since i2, ji, ki, li, mi, ni are all different, it follows that some one of them must be equal to i. This one may or may not be i. Suppose, first, that it is not so; but that, say, ji = i. Then j2i = j(ji) = ji = i. Thus j2 is some letter which multiplied into i gives i. But since this is true of j, it cannot, by our hypothesis, be true of any other letter, and it must be that j2 = j. Thus, if i2 is not i, there is some other letter whose square is the letter itself. We may assume, then, i to be that letter; and we shall have i2 = i. Then what will any other letter, say j, give when multiplied by i? Since i = i2, we have ij = i2j = i(ij). But according to our hypothesis, if j were not equal to ij, as the product, then ij could not be equal to i(ij), as it is. Hence ij = j, and similarly ik = k, il = l, im = m, in = n; and by like reasoning ji = j, ki = k, li = l, mi = m, ni = n. It is plain, then, that no other quantity can have its square equal to itself. For, if j = j while ij = j, we should have by our hypothesis i = j.
312. Since the product of two letters is a letter in every case, and since the number of letters is finite, it follows that some power of a letter is equal to some other power of the same letter. But suppose that jp = jp+q = jp - jq. But jp is equal to a letter and therefore, as we have seen, jp-i = jp. Thus, jp-i = jp-jq, where jq is likewise equal to a letter. But it is assumed that multiplication is invertible for the letters; so that jq = i. That is, some power of each letter is i. Moreover, jq-1 will also be equal to a letter; and j-jq-1 = jq-1-j = i. There is, therefore, for each letter some letter which multiplied by or into it gives i as the product; and since multiplication is invertible for the letters, there will be no other letter that multiplied either by or into that letter will give i as the product. Consequently, if the product of two letters is i, each of them is equal to some power of the other. If, then, two letters, say j and k, are not powers of one another, their product cannot be a power of either; for were j-k = kq, since multiplication is invertible for the letters, we should have j = kp-1, that is, j would be a power of k. If, then, there are two series of letters, the letters of each series, powers of one another, but no two letters of the one and the other powers of one another, then there must be a third series of which this is true; but any of these series may consist of a single square root of i. Of the five letters j, k, l, m, n, not more than three can be square roots of i. In the first place, all five of the letters j, k, l, m, n cannot be square roots of i. For if j2 = k2 = i then jk must be a different letter from either j or k. Call it l. Since then jk = l, we have lk = jk2 = ji = j and jl = j2k = ik = k. Moreover, if l2 = i, that is, if jkjk = i, multiplying into k we have kj = ikj = j2kj = j2kji = j2kjk2 = j(jk-jk)k = jl2k = jik = jk, so that kj = jk = l and lj = kj2 = ki = k, kl = k2j = ij = j. We thus find the products of j into i, j, k, l to be j, i, l, k, leaving nothing for jm to be except n. For, by hypothesis, it must be some letter different from the product of j into any of the other letters. But in like manner, the products of k into i, j, k, l would be k, l, i, j respectively; and the products of l into i, j, k, l, would be l, k, j, i, respectively; so that in each case we could only have jm = n, km = n, lm = n, violating the hypothesis that multiplication is invertible for the letters. That just four of the five letters, j, k, l, m, n, cannot be square roots of i is quite obvious. For what root of i could the fifth one be? It could not be a fourth root of i, since then its cube must be a separate letter; it could not be any other root of i, since then its square must be a separate letter; while all the other letters would be preoccupied. Indeed, for the same reason no root of i higher than the cube root (except, of course, a sixth root) can exist among the five letters. No more can two independent cube roots of i; although this is perhaps a trifle less obvious. Thus, the only possible cases are, first, where one of the letters is a sixth root of i, of which there are one hundred twenty varieties, {hoi polloi}, which vie with one another in their utter want of interest. The only remaining possible case is where there are three square roots of i and a cube root of i with its square, to which of course the same description applies. I here give the multiplication table.
If these signs were to be used in any general application, some of them would require modification to prevent their being mistaken for two or three characters. It will be remarked that i, j, k have each permutation in its own class indicated by the even or odd number of crossings in its character; while l, m, n reverse the class of each permutation.
313. In regard to the multiplication table, it is, in the first place, noticeable that if we take six new quantities, as follows:
| i'' = ((i-j)-(k-i))/3 | l'' = ((l-m)-(n-l))/3 |
| j'' = ((j-k)-(l-j))/3 | m'' = ((m-n)-(l-m))/3 |
| k'' = ((k-i)-(j-k))/3 | n'' = ((n-l)-(m-n))/3 |
| i''-j'' = i-j | j''-k'' = j-k | k''-i'' = k-i |
| l''-m'' = l-m | m''-n'' = m-n | n''-l'' = n-l; |
For example, i''+j''+k'' = 0 l''+m''+n'' = 0; while, without the accents, these equations would not hold good. But this very fact will lead us, in due time, to an analogy, not only very pretty, but of the highest importance for logic.
It is to be added that the multiplication table of i'', j'', k'', l'', m'', n'' is precisely the same as that of i, j, k, l, m, n, except that accents are everywhere added. But it is seriously important, both for the sake of the purely ideal beauty of this algebra, and still more in view of its great application to logic, that we should not allow its triadic purity to be violated. Now the reciprocal relation between the unaccented and the accented letters, were it allowed to stand alone, would be a purely dichotomic one. In order to avoid this, we ought to. introduce the following singly accented letters:
| i'=(j-k)/√-3 | i''=(j'-k')/√-3 | l'=(m-n)/√-3 | l''=(m'-n')/√-3 |
| j'=(k-i)/√-3 | j''=(k'-i')/√-3 | m'=(n-l)/√-3 | m''=(n'-l')/√-3 |
| k'=(i-j)/√-3 | k''=(i'-j')/√-3 | n'=(l-m)/√-3 | n''=(l'-m')/√-3 |
314. . . . In pure algebra, the symbols have no other meaning than that which the formulæ impose upon them. In other words, they signify any relations which follow the same laws. Anything more definite detracts needlessly and injuriously from the generality and utility of the algebra. It is that high principle which we all learned at a tender age that one cannot eat his cake and have it too; one cannot devote a thing to a particular use without making it less available for other applications. The logicians call it the principle of the inverse proportionality of comprehension and extension. Yet in this particular instance, we can adapt our doctrine better to thoroughgoing trichotomy by derogating a little from the dignified meaninglessness of pure algebra. In multiple algebra, it is generally assumed that the coefficients can be any numbers. My father, for example, even allowed them to be imaginary; though I cannot approve of that. But for the purposes of trichotomic mathematics, it should be recognized that each quantity has one of three values. Call them, for the moment, 0°, 120°, 240° — regarding 360° as the same as 0°. Or one might call them night, morning, and afternoon. Let us denote the three values by o (for {orthros}), δ (for {deilé}), ν (for {nyx}). Then, we must adopt the addition table:
| o+o = o | o+δ = δ | o+ν = ν |
| δ+o = δ | δ+δ = ν | δ+ν = o |
| ν+o = ν | ν+δ = o | ν+ν = δ |
For multiplication [a] table of these numbers will be obtained by assuming δδ = δ. Then δν = δ(δ+δ) = δδ+δδ = δ+δ = ν. δo = δ(ν+δ) = δν + δδ = ν+δ = o. For the sake of showing the consistency of the formulæ, we may complete the cycle
| δδ = δ(ν+ν) = δν+δν = ν+ν = δ; | |
| νν = ν(δ+δ) = νδ+νδ = ν+ν = δ, | (just as - - = +) |
| νo = ν(ν+δ) = νν+νδ = δ+ν = o | |
| oo = (ν+δ)o = νo+δo = o+o = o |
Instead of assuming the distributive principle in its entirety we might have evolved the multiplication table from these three equations
| oo = o | x(y+δ) = xy+x | (x+δ)y = xy+y. |
In the same spirit, the addition table might have been derived from the equations,
| o+δ = δ | δ+δ = ν | ν+δ = o | (x+δ)+y = x+(y+δ) = (x+y)+δ |
Thus,
o+ν = o+(δ+δ) = (o+δ)+δ = δ+δ = ν
o+o = o+(ν+δ) = (o+ν)+δ = ν+δ = o
ν+ν = ν+(δ+δ) = (ν+δ)+δ = o+δ = δ.
315. As for involution, until somebody can give me some good reason for attaching a given definite interpretation to (120°)(120°), I may be excused from attempting to introduce it into this algebra. I apprehend that, multiple algebra being essentially linear, there is no demand for any involution of its units.
316. It will be seen that, if we are to accept the premisses upon which the addition-table and multiplication-table are based, we cannot avoid giving peculiar properties to each of the three values δ, ν, o, and that the connection of them with some such sensuous images as day, night, and dawn is by no means an idle fancy. Let us put these tables into form. I add the subtraction-table
 |
 |
 |
| Addition Table | Multiplication Table | Subtraction Table |
We see that the multiplication-table recognizes a characteristic property in each member of the triad o, δ, ν. Multiplication by δ effects nothing. Multiplication by ν may have peculiar effects, but it is undone by a second multiplication by ν. Multiplication by ○ can never be undone, nor the same effect be otherwise produced.
317. We thus see that it is impossible to deal with a triad without being forced to recognize a triad of which one member is positive but ineffective, another is the opponent of that, a third, intermediate between these two, is all-potent. The ideas of our three categories could not be better stated in so few words. A man must be wedded to a system of metaphysics not to see the philosophical importance of the fact that these ideas thus insist upon intruding where we have done our best to bolt and bar the doors against them, by assuming the members of the triad to be more alike than three rain-drops.
318. What is experience? It is the resultant ideas that have been forced upon us. We find we cannot summon up what images we like. Try to banish an idea and it only comes home with greater violence later. Hence, we find the only wisdom is to accept, at once, the ideas that sooner or later we must accept; and we even go to work solicitous to find out what are the ideas which are going ultimately to be forced upon us. Three such ideas are the three categories; and it will be wise to pitch overboard promptly the metaphysics which preaches against them. To recognize the triad is a step out of the bounds of mere dualism; but to attempt [to deny] independent being to the dyad and monad, Hegel-wise, is only another one-sidedness.
319. We are not bound at all times to introduce the triad: it is not needed on every occasion. But we should be prepared to introduce it whenever it is needed. We must not absolutely restrict ourselves to the notion that two triads can at one time correspond to one another in only one way, so that a given member of the one must be down-right, absolutely connected with a given member of the other, or else be down-right, absolutely, disconnected from it — two alternatives differing as day from night — as {deilé} from {nyx}. We must be prepared, if occasion be, to admit a possible intermediate dawn. For to say that two things are disconnected is but to say that they are connected in a way different from the way under contemplation. For everything is in some relation to each other thing. It is connected with it by otherness, for example. We should, therefore, be prepared to say that two atoms, one of each triad, have either a positive connection, such as is under the illumination of thought at the time, or a dark other mode of connection, or a vague glimmering intermediate form of connection. Nor are we to rest there, as a finality. We must not restrict ourselves to saying absolutely that between a pair there either down-right is a given kind of connection, or down-right is not that kind. We must be prepared to say, if need be, that the pair has a δ-connection with a given mode of connection, or an opposite ν-connection with it, or a neutral o-connection with it. We can push this sort of thing as far as may be — indefinitely. Still, however far we carry it, ultimately there will always be a dichotomic alternative between the truth and falsity of what is said. Why it should be so, we shall see in the proper place and time for such an inquiry. At present, it is pertinent to note that the fact that it is so is forced upon our attention in pure mathematics.
320. Our algebra of i, j, k, l, m, n, supposes a triad to be in one-to-one correspondence with a second triad. We may conveniently identify that second triad with o, δ, ν; since these three values, by hypothesis, are any three things we please. As to the mode of connection of the first triad with o, δ, ν, we ought, in order to make full use of the algebra, to have a state of things which is, or is analogous to, a state in which each of the three things composing the triad is in two distinct modes connected with one of the three values, o, δ, ν; or with a value of whatever system of values may be appropriate. To indicate this we may use a sign like this
δ δ o
· · ·
ν δ ν
The three dots represent the triad. The letters above show what values are attached to the members of the triad in the first mode; the letters below show what values are so attached in the second mode. In order to translate this into the algebra, the values of the upper line, in their order, are to be taken as the coefficients of i, j, k respectively; those in the lower line as the coefficients of l, m, n respectively. Thus the sign written would be
δi+δj+ok+νl+δm[+νn.]
We may commonly write ○ for o, 1 for δ, -1 for ν. It often happens in the application of algebra that the absolute values of the coefficients are without significance, their ratios being alone important. If, in addition, the second mode of connection of the members of the triad with the values is identical with the first mode, we shall have
| i+j+k = o | l+m+n = o | |
| just as | i'+j'+k' = o | l'+m'+n' = o. |
Indeed it was the circumstance, that with the unaccented letters these equations do not generally hold good, which led me to the above remarks, which give an interpretation to a sum of letters of the algebra.
321. I have known such astounding blunders and oversights to be committed by the most powerful and exact intellects, that I have come to the conclusion that it is folly to attempt to set limits which human stupidity cannot overpass. Otherwise, I should venture to say that no intelligent reader of this chapter could, while wide awake, for two minutes harbor the notion that a transposition, or passage from one
permutation to another — the mathematicians call it a substitution — could possibly be the interpretation of a sum of transpositions; for the very idea of a multiple algebra is that a polynomial in the unit letters cannot be expressed as a numerical multiple of a single unit. A transposition produces a permutation in which all the members of the set are connected with different members of another set. In a sum of transpositions connections between members of two sets are created in which two or more of one set may be connected with one of the other. Precisely what such connections may be is sufficiently shown above. Another illustration is afforded by the diagram on page 260.
This is a sort of division table. The operand being entered on the right and the product on the left, the one operation effecting this transmutation is found at the intersection of the rows. We see that any permutation can be transmuted into any other, but by only one letter; and since there are only six letters in all while there are nine pairs composed each of a
member of each of two triads, no combination of letters can express every possible change of connections of the members of two triads (but only changes of permutations and their sums, as above explained). When it is requisite to be able to do that, as we shall find that for some logical problems it is, we must resort to another algebra published by me in 1870 †1 and for which I prefer the name novenions, rather than 'nonions,' the designation proposed by Clifford and employed by many mathematicians. Let u1, u2, u3, be three "umbræ," or ingredients of quantities. Then take
| i = u1:u1 | l = u2:u1 | o = u3:u1 |
| j = u1:u2 | m = u2:u2 | p = u3:u2 |
| k = u1:u3 | n = u2:u3 | g = u3:u3 |
and the multiplication table is as shown on page 261.
322. Sometime after my first publication, either my father or I myself (under the instigation of my father's ideas) transformed †P1 this algebra by means of the following equations, where, as above, {r} is an imaginary cube root of unity:
I = (u1:u1)+ (u2:u2)+ (u3:u3)
J = (u1:u1)+ {r}(u2:u2)+{r}2(u3:u3)
K = (u1:u1)+{r}2(u2:u2)+ {r}(u3:u3)
L = (u1:u2)+ (u2:u3)+ (u3:u1)
M = (u1:u2)+ {r}(u2:u3)+{r}2(u3:u1)
N = (u1:u2)+{r}2(u2:u3)+ {r}(u3:u1)
O = (u1:u3)+ (u3:u2)+ (u2:u1)
P = (u1:u3)+ {r}(u3:u2)+{r}2(u2:u1)
Q = (u1:u3)+{r}2(u3:u2)+ {r}(u2:u1)
323. Other points concerning trichotomic mathematics are more of logical than of mathematical interest, and are so woven with logic in my mind that I will not attempt to set them forth from a purely mathematical point of view. Here, then, I conclude what I have to say of these very simple branches of mathematics which lie at the root of formal logic. Those of which the interest is more purely mathematical must be treated in a very different manner in the next chapter. †1
Paper 8: Notes on the List of Postulates of Dr. Huntington's Section 2P †1
324. Dr. Huntington's Postulates at the head of section 2 of his paper †2 seem to me to have so great and so permanent an interest, that I am prompted to append to them some remarks with a view to establishing some other points of view which seem to me to be worth examining. My remarks inevitably present more or less opposition to Dr. Huntington's ideas; but that opposition is insignificant. For I certainly hold it to be undeniable that Dr. Huntington has successfully achieved his purpose; and that that purpose was a most important one for the study of logic. But in philosophy, as every student of it well understands, discoveries are worked out by reflection upon matters of common observation, instead of resulting from new opportunities for observation, as in all the positive sciences, or from pure thought concerning creations of the learned, as in mathematics, so that an idea is worthy of publication until one finds that it has not occurred to some profound student of the subject; and this one knows only by its opposition to something he has said.
325. By a 'postulate,' Dr. Huntington seems to understand any one of a body of propositions such that nothing can be deduced from one that could equally be deduced from another, while, from them all, every proposition of a given branch of mathematics might be deduced. The utility of such a body of premisses for the logical analysis of the branch of mathematics in question is beyond dispute. But I think we ought to distinguish between postulates and definitions. As for axioms, or propositions already well-known to the student who takes up the branch of mathematics in question, the ancients themselves admitted that they might be omitted without detriment to the course of deduction of the theorems. Indeed, an axiom could only be a maxim of logical nature. A postulate is a statement that might be questioned or denied without absurdity. A definition, or rather, one of the pair, or larger number, of propositions that constitute a definition, cannot be questioned, because it merely states the logical relation of a conception thereby introduced to conceptions already in use. It is quite true, on the one hand, that a postulate, after all, is merely a part of the definition of the underlying conception of the branch of mathematics to which it refers, (Euclid's celebrated fifth postulate, for example, being merely a part of the definition of Euclidean space); while on the other hand, a definition is a statement of positive fact about the use of the word defined, and may thus be regarded as a sort of postulate. But to argue from these truths that there is no important difference between a postulate and a definition would be to fall into a fallacy of a very common kind, that of denying all important difference between two things because they are in an important respect alike, or of denying all important likeness between two things because they are in an important respect unlike. There is a vast difference between the logical relations to a branch of mathematics of propositions defining its very purpose in defining its fundamental hypothesis, and those of propositions that merely define conceptions which it is convenient or even which it is necessary to introduce in order to develop that branch.
326. I shall consider only the postulates of Dr. Huntington's section 2. This section refers to a special form of the Boolian algebra of logic. The algebra which Boole himself used was simply ordinary numerical algebra as applied to a collection of quantities each of which was assumed to be subject to the quadratic equation x(1-x) = 0, and Boole showed how this hypothesis could be applied to the solution of many logical problems. For him, therefore, addition and multiplication were nothing but the numerical operations, greatly restricted in their application. An essential, not to say the vital, element of Boole's method lay in its applicability to the calculation of probabilities and statistical relations. But this feature disappeared in the algebra as it was modified by all his followers except Mr. Venn, a circumstance that gives a special value to Venn's Symbolic Logic, a work that has many other merits. The rest of us assigned to the terms and operations purely logical meanings which we thought had sufficient analogy with the numerical conceptions to receive either exactly the same symbols, or, in my own case, to receive symbols closely resembling the numerical symbols. We †1 made three changes which affected the working of the method. These were as follows: †2
First, we introduced what we inappropriately called 'logical addition,' writing something exactly or nearly like x y for what Boole wrote as x+y+xy.
y for what Boole wrote as x+y+xy.
Second, we introduced the copula of inclusion, writing
x ⤙ y
where Boole would write
x = xy.
Third, we introduced the negative of this copula; writing
~(x ⤙ y)
for what Boole had no correct way of writing except "x = xy is false."
327. Now the Boolian algebra to which Dr. Huntington's section 2 relates is Boole's as modified in the first two of these ways. It is to be added, moreover, that Schröder, with the majority of the Boolians, abandoned Boole's conception that every logical term has one or other of two values. For my part, I have always retained that conception, as far as non-relative terms go, which correspond to the quantities of ordinary algebra. But I introduced relative terms which correspond to what Sylvester called the umbræ of quantities (the conception is due to Leibniz), and employed various signs of operation upon these umbræ. †3 At the same time I showed that a non-relative term can be considered as a relative, that, in another sense, a relative term may be considered as non-relative, and that the non-relative operations equally apply to relatives. †4 I regard a logical term as an indefinite proposition or blank form of proposition; man, for example, meaning "x is a man." Now every proposition has one or other of two values; the lesser, that of being false; the greater, that of being true. A term, or rheme, is like 0/0, in itself indeterminate in value, yet having one or the other of two values in each particular case. Thus, when in the ordinary Boolian algebra we write m ⤙ l, meaning "every man is a liar," according to me this means "if x (which is any individual object you may choose) is a man, then x is a liar," m signifying that x is a man, and l, signifying that x is a liar. Schröder, on the other hand, would say that m 'denotes' the entire collection of men (though I do not know what definite idea can be attached to the word 'denotes'), that l 'denotes' the entire collection of liars, and that the formula states that the former collection is included in the latter. Now it is certain that Dr. Huntington does not embrace my conception, since he would have greatly simplified his list of postulates if he had done so; but it is not clear that he unequivocally rejects this conception.
328. In my opinion, in algebra generally, the distinction between a quantity and an operation is a subsidiary one, and that we ought to allow operations to be operated upon as much as quantities; and this, perhaps, will be commonly conceded. If so, in the algebra of logic, the signs of the so-called logical addition and multiplication are substantially nothing but relative terms of a special description. But I would allow the spirit of unification to have the further effect that no radical separation be recognized between signs of operation and copulas, such as = and ⤙ . Thus, in any paper of 1880, †1 I have such expressions as (a ⤙ b) ⤙ (c ⤙ d) which is equivalent to
or to
Dr. Huntington evidently does not contemplate any such handling of the algebra of logic.
329. Dr. Huntington's purpose is, while considering the Boolian algebra in a purely morphic light, without regard to its interpretation, to draw up a list of independent propositions which shall justify every illative transformation of the algebra in one way, and in one way only. Of his postulates, which are ten in number, the first three give a morphic definition of the copula  which is the purely morphic generalization of the copula of inclusion, these three propositions also showing that the algebra regards all entities as interchangeable which a direct application of this copula would not distinguish. The next two postulates define the two terms which I regard as the two values. The next two amount (according to my well-known definitions of the logical aggregate and compound) †1 to asserting that any terms may be logically added and multiplied. The eighth and ninth morphically define the sign of negation. The tenth is the morphic generalization of the logical postulate that it is possible to express a proposition that is false.
which is the purely morphic generalization of the copula of inclusion, these three propositions also showing that the algebra regards all entities as interchangeable which a direct application of this copula would not distinguish. The next two postulates define the two terms which I regard as the two values. The next two amount (according to my well-known definitions of the logical aggregate and compound) †1 to asserting that any terms may be logically added and multiplied. The eighth and ninth morphically define the sign of negation. The tenth is the morphic generalization of the logical postulate that it is possible to express a proposition that is false.
330. Perhaps this arrangement has not been the subject of much consideration. In defining any branch of mathematics, I should begin with stating the multitude of values it admits; and therefore in this case I should put postulate No. 10 first. Dr. Huntington seems to have left it to the last because he considered it "trivial." But it is certainly not trivial in the sense of being inessential. If it were it should be omitted altogether. Indeed in the sense in which it is trivial, this is the character of the whole algebra. In the sense in which the algebra is of interest and significance, its having just two values is its most significant and characteristic feature. If he had begun with the statements
There are at least two expressions not interconvertible, Z and I.
Every expression, a, is so related to Z, that a  Z may be written alone.
Z may be written alone.
Every expression, a, is so related to I, that I  a may be written alone.
a may be written alone.
Every expression, which is such that, taking any expression that is a part of it, the whole could permissibly be written alone whether Z or I were substituted for this part, may be written alone. †2
Paper 9: Ordinals †1
331. . . . I pay full homage to Cantor. He is indisputably the Hauptförderer of the mathematico-logical doctrine of numbers. As for Dedekind, his little book Was sind und was sollen die Zahlen? is most ingenious and excellent. But it proves no difficult theorem that I had not proved or published years before, and my paper †2 had been sent to him. His definition †3 of an infinite collection is precisely my previous definition of a finite collection reversed. †4 His introduction of Gauss's concept of the Abbild, †5, which has been spoken of as something quite great, might have been borrowed from my paper, though I made no fuss about it. Since my priority about the distinction of the finite and the infinite has been pointed out in Germany, in a prominent way, †6 Dedekind has said that he had the idea some years earlier. He seems to think this an important circumstance. I may mention that my habit has always been to record ideas that seemed to me valuable in a certain large blank book with the dates at which I set them down, almost always not until I had had the ideas long enough to be quite convinced of their value. This idea about finite and infinite collections was thought worthy of record. †7 But I do not see that it has any interest for anybody but myself; and from Dedekind's conduct, I infer he would prefer I should not give it.
332. An extremely difficult question about whole numbers is as to which are the more fundamental, ordinal numbers or the cardinal numbers considered as expressing the multitudes of collections. The solution of this problem is contained in the following six propositions, which are all capable of proof. †1
First. The general idea of plurality is involved in the fundamental concept of Thirdness, a concept without which there can be no suggestion of such a thing as logic, or such a character as truth. Plurality, therefore, is an idea much more fundamental than that of the ordinal place of a member of a linear series.
Second. The conception that there is a transitive relation of greater and less among multitudes is logically prior to the conception of ordinal place in a linear series. But that relation of greater and less is by no means Bolzano's relation †2 which is at the foundation of the doctrine of multitude. Nothing more in the way of a conception of greater or less collections is involved in the concept of ordinal place than the idea that the greater collection can result from the incorporation into the lesser collection of another collection (using this word in a sense in which a collection may have but a single member).
Third. Cantor †3 represents the two ways in which a unit may be added to an endless series, namely by incorporation into the series, or by immediately following the endless series, as differing only in respect to the order of performance of the addition. But this is incorrect. The original concept of greater involved in the general concept of ordinal place is that of incorporation into a series. A contradiction is involved in speaking of a unit being incorporated into an endless series after all the members of the series, as well as in speaking of an endless series being incorporated into a finite series. The concept of a unit coming immediately after the endless series is a different concept.
Fourth. Both the concept of incorporation into a series and of attachment immediately after an endless series are involved in the complete conception of ordinal quantity; but they do not suffice to make it up. They do not even make up the full concept of what Cantor calls a well-ordered series, †4 but which I propose to call a Cantorian series, in order to pay due honor to the completer of the doctrine of ordinal quantity, by attaching his name to this invaluable concept. This concept does not of itself make up the concept of ordinal quantity, but it is its most important ingredient.
Fifth. Bolzano's concept †1 of being multitudinally greater than is in no way involved in the concept of ordinal quantity.
Sixth. The concept of multitudinal quantity does not involve the concept of ordinal quantity as a system, nor even that of an ordinal quantity; but it does involve every ingredient of the concept of ordinal quantity except the subjectal abstraction of it. The logical term subjectal abstraction here requires a word of explanation; for there are few treatises on logic which notice subjectal abstraction under any name, except so far as to confuse it with precisive abstraction which is an entirely different logical function. †2 When we say that the Columbia library building is large, this remark is a result of precisive abstraction by which the man who makes the remark leaves out of account all the other features of his image of the building, and takes [to represent the size] the word "large" which is entirely unlike that image — and when I say the word is unlike the image, I mean that the general signification of the word is utterly disparate from the image, which involves no predicates at all. Such is precisive abstraction. But now if this man goes on to remark that the largeness of the building is very impressive, he converts the applicability of that predicate from being a way of thinking about the building to being itself a subject of thought, and that operation is subjectal abstraction. Subjectal abstraction is one of the most constantly employed tools of the mathematician. In thinking of the system of multitudinal quantity, we do not need to think about ordinal quantities, but we do need to attribute, to the objects we are thinking about, ordinal places in a series. The very system of multitudinal quantities themselves consists in their being ordinally arranged.
333. It is indispensable to my argument about continuity that I should, at this point, give a formal definition of the system of finite numbers, regarded as ordinals. I will give two such definitions. The first is new, and is, I think, the best definition yet given of the finite ordinals, although because of its novelty I find the second handier, which was substantially given by me in 1883. †1 I may mention that in a paper of mine published in 1867, †2 I attempted a definition of the cardinal numbers considered as multitudinal. But although I received some complimentary letters about that paper at the time, it is now utterly unintelligible to me, and is, I trust, by far the worst I ever published. Nevertheless, it is founded upon an interesting idea, worthy of a better development; and the curious contrast between all the operatives of arithmetic when viewed multitudinally and when viewed ordinally is also worth showing.
In both these definitions, for the sake of simplicity, I speak of 'ordinals' meaning finite ordinals, or places in a simple endless series. Also when I speak of a definition of ordinals what I mean is a definition of the system of relations between ordinals.
334. If a denote a character, then what I should mean by calling it an ordinary character would be that it would be absurd to say of two imaginary objects, M and N, that M possesses α while N does not possess it, but that in respect to all other characters — or in respect to all other characters of a given line of characters — M and N do not differ. For ordinary characters so blend into one another that no one can be singled out. It is not in their nature. By a singular character on the other hand, I mean a character which differs decidedly from every other however nearly like it. A branch character is a singular character which belongs to a certain collection of characters which I call a system of branch characters, and the characteristic property of such a system is as follows:
Let α and β be any two different characters of the system whatsoever, then of the three propositions:
P possesses both α and β
Q possesses α but not β
R possesses β but not α
one or other is contrary to the nature of things, even of imaginary things, while two of the three propositions (as the proposition "S possesses neither α nor β") are possible as far as the nature of the characters go. Understand then, that if of a system of singular characters it is possible to find among them two such (say beauty and virtue) that all that triad of propositions might be true of different imaginary objects, that system of characters is not a system of branch characters. Again if a system of singular characters be such that it is possible to find any two of them (like being a prime number and exactly dividing the number next greater than the continued product of all smaller integers) so related that two of those three forms of proposition would be contrary to the nature of the characters, that system is not a system of branch characters. Once more if a system of singular characters be such that it is possible to find among them any two of such a nature that both could not be absent from any object, that system is not a system of branch characters. Finally, if it be possible to find in a system a single ordinary character, it is not a system of branch characters. But if none of these four things be possible it is a system of branch characters.
The reason I call these branch characters is that a collection of characters each of which consists in being on some one branch of a tree forms for small objects like insects, as subjects, a system of branch characters, for if the two branches are separate nothing can be on both, but a thing may be on either and not on the other, or it may be on the trunk and so not on either. The only case in which a thing can be on two branches at once is when one branch is itself on the other, so that to be on the former is ipso facto to be on the latter. But then it cannot be on the former and not on the latter, though it may be on the latter and not on the former.
335.
First Definition of Ordinals
Clause 1. Of any two non-identical ordinals, there is a branch character of a certain system of branch characters (here to be designated simply as 'the system') which one of them possesses while the other lacks it.
Clause 2. The branch characters of the system are singular.
Clause 3. It would be logically possible for an object susceptible of any branch character of the system, and actually having one of them, to change to one other, and to change from every character, to which it had been changed, to one branch character of the system to which it had never been changed, without ever being restored to its first character.
Clause 4. On the other hand, this would be logically impossible if the changes were restricted to those branch-characters of the system that are possessed by any one ordinal.
Clause 5. (From clauses 3 and 4 it follows that every branch character of the system has at least one other immediately dependent upon it; that is, dependent upon it, but not dependent on a third that is dependent upon it), but no branch character of the system has more than one immediately dependent upon it.
Clause 6. Every combination of possession and nonpossession of branch characters of the system which is logically consistent with clauses 1 to 5 inclusive and with the definitions of branch characters, dependence, etc., is actually realized in some ordinal; (and that ordinal which possesses none of the branch characters of the system is called zero).
336. The statement of the second definition will be facilitated by the explanations of three peculiar locutions. In order to abbreviate oft-recurring phrases like 'A stands in the relation r to B,' we may say indifferently either 'A is r to B' or 'B is r'd by A.' We may say that a relation, r, is an appurtenance, if, and only if, it is out of the nature of things for anything to be r to two different correlates. We may call a relation, r, a comparative fulfillment, if, and only if, to say that A is r to B is the same as to say that A is not r'd by anything that r's B, or nothing is r to A that is not r to B. Thus, to say that 'John' is as short a word as 'Jack' is the same as to say that nothing is as short as 'John' that is not as short as 'Jack.'
Second Definition of Ordinals
Clause I. The most fundamental relation of ordinals, N, ('next after'), is an appurtenance.
Clause II. Every ordinal is N'd by an ordinal.
Clause III. There is an ordinal, zero, or 0, that is not N to any ordinal.
Clause IV. The relation g (as high as) is a comparative fulfillment.
Clause V. Whatever ordinal is N of an ordinal is g of that ordinal.
Clause VI. Whatever ordinals p and q may be, either the facts that certain ordinals are N to certain ordinals, taken in conjunction with the preceding clauses of this definition, logically necessitate p's being g to q, or else p is not g to q.
Clause VII. Whatever ordinals p and q may be, either p is g to q or q is g to p.
If we translate either definition into the terms of the other all its clauses may be deduced from those of the other. Thus, the branch characters of the system are the characters of being N to an ordinal that is g to a, where a is any one ordinal, constant for any one branch character but varying with the branch character. On the other hand, to say that n is g to m is the same as to say that n possesses every branch character of m, while to say that n is N to m is to say that n possesses a branch character, say ν, not possessed by m, while whatever branch character that is not ν and is not possessed by m, ξ; may be, n does not possess ξ;. The demonstration of each definition by the other will be found an instructive exercise, but it need not be worked out for our purposes. A person who wishes to try it should begin by proving by the second definition that no ordinal is N to itself (for in Clause II it is not said that every ordinal is N'd by another), and that no two different ordinals are N to the same ordinal (for this is not implied in any single clause of the definition).
337. All that it is necessary to insist upon here is that the only thing that whole numbers can express is the relative place of objects in a simple, discrete, linear series; and whole numbers are applicable to enumerable multitudes and enumerable collections, only because it happens that those multitudes have each its place in a simple, discrete, linear series. It is true that Dr. Georg Cantor, the great founder and Hauptförderer of the logico-mathematical doctrine of numbers, begins his exposition with what he calls "cardinal numbers," †1 but which ought properly to be called multitudes. For cardinal numbers proper are nothing but the vocables of a certain series of vocables that are used in the operation of ascertaining the multitude of a collection, by counting, and thence are applied as appellatives of collections to signify their multitudes. Multitude itself, however, belongs to various different collections in various different grades, where cardinal number has no application, at all. Cantor, †1 however, has partially shown, what is entirely true, that the whole doctrine of multitude can be developed without any reference to ordinal numbers. But in treating of ordinals we are obliged to say, in substance, what their multitude is. Thus, when we look at the matter from a certain point of view, it seems that the doctrine of multitude is more fundamental than that of ordinals, and that all whole numbers really express multitudes. But this is a logical fallacy. That the concepts of multitude and of ordinal place in a simple, discrete, linear series are very intimately connected is true. The latter involves the consideration of facts constituting the applicability of definite conceptions of multitude; but it does not involve these conceptions themselves. Multitude, on the other hand, is nothing but the place of a series in one or the other of two simple, discrete, linear series, and it is impossible to define it at all without the use of the ordinal conception itself.
That positive whole numbers can express nothing but places in a linear series is proved by the fact that from either of the definitions above of ordinals, neither of which involves any concept not involved in the concept of such a series, any property of whole numbers can be deduced. If the statement of the property involves the triadic relation of being 'sum of' or being 'product of' of course this relation must first be defined. In case the first definition is used, N being defined in terms of branch characters as above, and in case the second definition is used, without that definition of N, the definition of sum is as follows:
Any ordinal, s, is a sum of an ordinal m as summand, and an ordinal n as addend, if, and only if, either m is N to an ordinal, l, and s is N to an ordinal that is a sum of l and n, or m is not N to any ordinal, and s is n.
A product may be defined thus: An ordinal, p, is a product of an ordinal as multiplier and of an ordinal as multiplicand, if, and only if, either the multiplier, m, is N to an ordinal, l, and p is the sum of the multiplicand, n, and of an ordinal that is a product of l and n, or else m is not N to any ordinal, and p is m.
338. Many a person who will readily admit that whole numbers can express nothing but places in a linear series is inclined to insist that with fractions it is otherwise, fractions essentially involving the idea of equality of measure among the parts of a whole. Indeed, more than one highly esteemed writer might be named who has emphasized this as an essential characteristic of fractions, and in support of the assertion has averred that fractions cannot be added or subtracted until they have been reduced to a common denominator, and indeed that until that is done one cannot always tell which of two fractions is the larger. It thus becomes necessary to enter upon a proof that what is true of whole numbers is equally true of fractions; namely, that they can express nothing but relative places in a linear series; and this shall be done by defining first the system of rationals, or rational quantities, and then the system of fractional expressions, without any reference to measure, purely in terms of the relations of linear series, and in showing that from these definitions all properties of rationals and of fractions can be logically deduced.
339. In order to do this it becomes convenient, and indeed little short of indispensable, to make use of the secundal system of numerical notation, which may be familiarly described as a system exactly like the Arabic notation, except that Two is taken as the base of numeration instead of Ten. It may be formally defined as follows:
1. There is a collection of objects called secundal places (not places of secundals, which are used only in fractional expressions), and this one collection of places is the same for all secundal numerical expressions.
2. Every secundal place is in a certain relation to an ordinal called being designated by that ordinal, and is designated by no other ordinal.
3. Every ordinal designates a secundal place, and designates no other secundal place.
4. Every secundal integer expression denotes an ordinal and denotes no other ordinal.
5. Every ordinal is denoted by a secundal integer expression and is denoted by no other secundal integer expression.
6. Every secundal integer expression is a system of perceptual objects, called figures, each having perceptual characters in itself, and each having a perceptual relation to each secundal place.
7. In every secundal integer expression each figure has a perceptual relation to a secundal place, called being in that place, and is in no other place.
8. In every secundal integer expression, every secundal place has a figure in it and has no other figure in it.
9. In every secundal integer expression, the figure in each secundal place is perceptually distinguishable as having a certain character, called being a unit, or as not having that character, when it is called a blank. . . .
10. In every secundal integer expression, there is a secundal place, such that in every secundal place that is g to it there is a blank;
11. Every secundal expression denoting an ordinal n that is N to an ordinal, m, is such that:
Firstly, some figure of it is a blank.
Secondly, in that secundal place, to which every place that is g contains a blank in the secundal expression for m, in the secundal expression for n there is a unit.
Thirdly, in every secundal place to which that place is N[g] there is a blank in the expression for n instead of the unit there in the expression for m.
Fourthly, in every secundal place that is N[g] to that place the figure in the expression for n has the same character as the figure in the same place in the expression for m.
It is usual to write those blanks to whose places the place of some unit is N[g] as 0, leaving those of which this is not true unwritten. The figure in the 0 place is best drawn with heavy lines.
340. The system of rationals, or positive rational quantities, may now be defined as follows:
1. Every rational is in a certain triadic relation to an ordinal called its antecedent, and to an ordinal called its consequent, namely, the relation of being the ratio (for the sake of brevity, I omit the qualification in lowest terms) of the antecedent to the consequent; but is the ratio (in lowest terms, always) of no antecedent to any other consequent, nor of any other antecedent to any consequent. Nor is any other rational a ratio of the same antecedent to the same consequent. But not every two ordinals are the antecedent and consequent of a rational (in lowest terms).
2. Every ordinal is a rational, being the ratio of itself as antecedent, to NO (the ordinal that is N to zero, which in the secundal notation is written 1).
3. The relation g may be taken in a generalized sense, so as to be applicable to all rationals. Writing g' for this more general relation, every ordinal that is g to an ordinal, is also g' to the same ordinal, and if any rational be g' to an ordinal that is g to an ordinal, the first rational is g to the latter ordinal, and if an ordinal be g to an ordinal that is g' to a rational, the former ordinal is g' to the last rational.
4. If the converse of the negative of g' be called γ (being greater than) every rational stands to any non-identical rational either in the relation of being γ to it or in that of being γ'd by it.
5. There is a peculiar relation, to be here called being indicated by or having as indicator, in which every rational stands to a secundal integer expression, and to nothing else.
6. Every secundal integer expression is indicator of a rational, but of no other rational.
7. If from the indicator of any rational, on the one hand, the figure in the zero secundal place be struck off and the result be called the near subindicator, and on the other hand all those figures be struck off which are in places g'd by the place of that figure unlike the figure in the zero place whose place is g'd by all the figures unlike the figure in the zero place and call the result the far subindicator, then unless the far subindicator contains no unit, the irrational of the first indicator has for its antecedent the sum of the antecedents of the rationals indicated by the near and far subindicators and for its consequent the sum of the consequents of the same rationals; but if the far subindicator contains no unit, the antecedent of the first rational is N to the antecedent of the rational indicated by the near subindicator, and its consequent is the ordinal that is N to 0.
8. The rational whose indicator is zero is zero.
It now becomes easy to arrange the rationals in order of their magnitudes. The table on preceding page shows a few of them, [with] the rationals under the indicators.
I will now give the antecedents, or numerators, only for the right-hand-half of the table in Arabic figures.
The objection that there is no way of finding out which of two fractions is the greater without reducing them to a common denominator is an amusing self-betrayal; for all good arithmeticians proceed by setting down the two fractions side by side and then subtracting numerator from numerator and denominator from denominator, putting down the remainders, as a new fraction on the side of the fraction with larger terms, and so continuing until one has 0/1 at one end of the row and 1/0 on the other. For (1/0)>(0/1). This can always be done if a little ingenuity varies the process a little. Thus, which is the greater 487/830 or 301/513?Proceed thus
This series everywhere increases in the same direction. Hence 487/830 > 301/513. Fractions can be added on the same principle.
Paper 10: Analysis of Some Demonstrations concerning Definite Positive IntegersP †1
341. Let the Universe of 1. c. italics be the aggregate of all definite Integers not negative. Let the Universe of Greek Minuscules be the aggregate of possible characters of such Integers. Let qαu mean, as in 3.398, that the Integer, u, has the character, α.
Hypotheses
(1) ΠαΣβΠu (qαu qβu)·(q̄αu
qβu)·(q̄αu q̄βu) i.e., every character has a negative.
q̄βu) i.e., every character has a negative.
(2)ΠαΠβΣγΠu(q̄αu q̄βu
q̄βu qγu)·(qαu·qβu
qγu)·(qαu·qβu q̄γu) i.e., of every two possibilities there is a compounded possibility. Instead of introducing an unanalyzed relation of 'as small as,' let us, at first, conceive a character of characters, consisting in each of certain characters belonging to every integer lower than an integer to which it belongs.
q̄γu) i.e., of every two possibilities there is a compounded possibility. Instead of introducing an unanalyzed relation of 'as small as,' let us, at first, conceive a character of characters, consisting in each of certain characters belonging to every integer lower than an integer to which it belongs.
(3) ΠuΣαqαu·sα, †2 every Integer has a character common to all lower Integers. (A formal proposition.)
(4) ΠaΣus̄α q̄αu i.e., there is no highest Integer.
q̄αu i.e., there is no highest Integer.
(5) ΣuΠαΠv qαu s̄α
s̄α q̄αv i.e., there is a lowest Integer (i.e., Zero).
q̄αv i.e., there is a lowest Integer (i.e., Zero).
(6) ΠαΠβΠuΠv s̄α s̄β
s̄β q̄αuqβu
q̄αuqβu qαvq̄βv i.e., an Integer having any s-character that another has not has every one that other has.
qαvq̄βv i.e., an Integer having any s-character that another has not has every one that other has.
(7) ΠuΠvΣαΠβ sα·(qαu qαv)·(q̄αu
qαv)·(q̄αu q̄αv)
q̄αv) qβu·qβv
qβu·qβv q̄βu·q̄βv i.e., unless one of any two integers has an s-character which the other has not, they are alike in all characters, and therefore, being definite, are identical.
q̄βu·q̄βv i.e., unless one of any two integers has an s-character which the other has not, they are alike in all characters, and therefore, being definite, are identical.
(8) ΠuΣαΣvΠwΠβΠγ qαu·sα·q̄αv·(s̄β q̄βu
q̄βu qβw
qβw s̄γ
s̄γ q̄γw
q̄γw qγv) i.e., every integer has another next higher. This is a consequence of the following with (4):
qγv) i.e., every integer has another next higher. This is a consequence of the following with (4):
(9) ΠαΠuΣvΠwΠβ q̄αu qαv·(q̄αw
qαv·(q̄αw s̄β
s̄β q̄βw
q̄βw qβv) i.e., every class of integers has a lowest member.
qβv) i.e., every class of integers has a lowest member.
For formula (10) see below [343].
| Addition |
Let (i+j)k mean that the integer k can result from adding the integer i to the integer j. This can be negatived by an obelus over it like any other expression.
Addition is definable by the following six formulæ:
(11) ΠiΠjΣk(i+j)k
(12) ΠkΠjΣiΣα sα·qαj·q̄αk (i+j)k
(i+j)k
(13) ΠiΠkΣjΣα sα·qαi·q̄αk (i+j)k.
(i+j)k.
(14) ΠiΠjΠkΠuΠvΠwΣαΠβ~(i+j)k ~(u+v)w
~(u+v)w  sα·(qαu·q̄αi
sα·(qαu·q̄αi qαv·q̄αj)
qαv·q̄αj) s̄β
s̄β q̄βw
q̄βw qβk
qβk
(15) ΠiΠjΠkΠuΠvΠwΣαΠβ~(i+j)k ~(u+v)w
~(u+v)w  sα·(qαv·q̄αj
sα·(qαv·q̄αj qαw·q̄αk)
qαw·q̄αk) s̄β
s̄β q̄βu
q̄βu qβi
qβi
(16) ΠiΠjΠkΠuΠvΠwΣαΠβ~(i+j)k ~(u+v)w
~(u+v)w  sα·(qαu·q̄αi
sα·(qαu·q̄αi qαw·q̄αk)
qαw·q̄αk) s̄β
s̄β q̄βv
q̄βv qβj
qβj
342. It would be illuminating to exhibit the above fifteen propositions scribed in existential graphs; †1 but it would be aside from my present purpose. I proceed to indicate sketchily in what manner the leading theorems concerning the addition of positive integers can be deduced from the fifteen propositions by means of the rules given in 3.396. (Though those rules might now be amended much, so as to render them more efficient.) If (14) be iterated, it becomes
ΠiΠjΠkΠuΠvΠwΣαΠi'Πj'Πk'Πu'Πv'Πw'Σα'Πβ Πβ'{~(i+j)k ~(u+v)w
~(u+v)w sα·(qαu·q̄αi
sα·(qαu·q̄αi qαv·q̄αj)
qαv·q̄αj) s̄β
s̄β q̄βw
q̄βw qβk}·{~(i'+j')k'
qβk}·{~(i'+j')k' ~(u'+v')w'
~(u'+v')w' sα'·(qα'u'·q̄α'i'
sα'·(qα'u'·q̄α'i' qα'v'·q̄α'j')
qα'v'·q̄α'j') s̄β'
s̄β' q̄β'w'
q̄β'w' qβ'k'.
qβ'k'.
Next (I go into detail with this first example farther than I shall with others), we may, by the fifth rule, identify u, i', and u', with i; v, j', and v' with j; k' with w; w' with k; and β' with β (for though the rule as given in the memoir is the right one, theoretically, yet in practice the operation of this and part of the sixth can generally be reduced with convenience to the identification of the index of any Π with any index to the left of it in the quantifier). We, at the same time, apply Rule 6 somewhat, remembering that qαi·q̄αi  0 etc. and applying the principle (A
0 etc. and applying the principle (A B)·(A
B)·(A C) = A
C) = A B·C, and then applying Rule 7 we get
B·C, and then applying Rule 7 we get
ΠiΠjΠkΠwΠβ~(i+j)k ~(i+j)w
~(i+j)w s̄β
s̄β (q̄βw
(q̄βw qβk)·(q̄βk
qβk)·(q̄βk qβw) or
qβw) or
ΠiΠjΠkΠwΠβ~(i+j)k ~(i+j)w
~(i+j)w s̄β
s̄β q̄βw·q̄βk)
q̄βw·q̄βk) qβw·qβk).
qβw·qβk).
Let us now compound this with (7) in which, to avoid confusion, we may write m for u, n for v, υ for α, and φ for β. We thus get
ΠmΠnΣυΠφΠiΠjΠkΠwΠβ {~(i+j)k ~(i+j)w
~(i+j)w s̄β
s̄β q̄βw·q̄βk)
q̄βw·q̄βk) qβw·qβk)} {sυ·(qυm
qβw·qβk)} {sυ·(qυm qυn)·(q̄υm
qυn)·(q̄υm q̄υn)
q̄υn) qφm·qφn
qφm·qφn q̄φm·q̄φn}.
q̄φm·q̄φn}.
Now identifying β with υ, w with m, k with u, the formula with an obvious reduction of the Boolian, becomes
(17) ΠmΠnΠφΠiΠj ~(i+j)n ~(i+j)m
~(i+j)m qφm·qφn
qφm·qφn q̄φm·q̄φn i.e., if (i+j)m and (i+j)n, then m = n; or the sum of two definite positive integers has but a single value.
q̄φm·q̄φn i.e., if (i+j)m and (i+j)n, then m = n; or the sum of two definite positive integers has but a single value.
Without writing down the formulae, a little close attention will enable one to convince himself that (15) and (16), treated almost exactly as (14) has been above, show that if
(18) (i+j)k and (u+j)k then u = i and that
(19) if (i+j)k and (i+v)k then j = v.
343. Abbreviations. Having thus illustrated how the notation works, it will be well to introduce some abbreviations.
First, although obviously indefinite individuals may be alike in respect to every character, yet different in their (real or pretended) brute existence, such as the different parts of space and the different vertices of the regular dodecahedron of pure mathematics, still since the Universe of l. c. italics is confined to definite integers, we may, by introducing |ij to mean that i and j are the same individual, write the following principle:
(10) ΠuΠvΣαsα·(qαu qαv)·(q̄αu
qαv)·(q̄αu q̄αv)Ψ|uv.
q̄αv)Ψ|uv.
Of course, the negative of |ij will be ⊤ij.
344. One may entertain the theory that all vagueness is due to a defect of cogitation or cognition. It is a natural kind of nominalism the justice of which it would be remote from the purpose of this analysis to consider. The vagueness of characters is of different kinds. The quality of redness and the quality of blueness differ without differing in any essential character which one has but the other lacks. The otherness of them is as irrational as the qualities themselves, if not more so. It appears to consist in a mutual war between them, in our taste. But the characters of integers are not of this irrational kind. In another regard, however, they are vague. Thus we say that the two characters of 4, of being the sum of 2 and 2, and of being the product of 2 and 2, are different characters, so that we cannot, in imitation of (10), write
This is because we do not think out the meaning of 2+2 and 2×2 to the very bottom. In this respect, the objects we denote by Greek minuscules are not generally definite.
345. The character, |, which I introduced in 1882, when I was teaching logic in the Johns Hopkins University, was in my mind one of a class of notations which I left unmentioned in order that some one of my pupils might have the pleasure of finding it out for himself; but as nobody has, so far as I have noticed, in the three-fourths of a generation that has elapsed, I will give some illustrations of the class:
|ij means j is a member of the singlet, i.
2ij means j is a member of the doublet, i, or unordered pair, or couple.
3ij means j is a member of the triplet, i, or unordered trio, or leash.
4ij means j is a member of the quadruplet, i, or unordered collection of 4.
9ij means j is a member of the nonuplet, i, or unordered collection of 9.
xij means j is a member of the decuplet, i, or unordered collection of 10.
Ordered collections I call, medads (0), monads, dyads, triads, etc. Indeterminate as to being ordered are binion (or pair), trine, quaternion, quine, senion, septene, octone, novene, dene (or denion), etc.
By an ordered collection, I mean one of which each member has a peculiar relation to the whole; as for example, if one is definitely the first, another definitely the second, a definite one the third, etc., or if there is any other formal relation by which each is different from all the others. There are also diduct collections which are formally divided into subcollections and it may be in more than one way, whether inadequately, adequately, or superfluously. By adequately, I mean just sufficiently to make the collection an ordered one.
With this notation (7) can be expressed as follows, using Hebrew letters to denote definite collections:
ΠℵΣiΣjΣα 2ℵi·2ℵj·sα·qαi·q̄αj
The utility of the symbols 1, 2, 3, etc. is increased by employing them as follows: |i, |ij, |ijk, etc. means that the indices denote the same existing individual.
2ℵi, 2ℵij, 2ℵijk, etc. mean that the individuals denoted by the indices belong to the doublet ℵ.
2ijk, 2ijkl, etc. mean that all the individuals denoted by the indices are members of one doublet.
(2· ⊤ )ij, (2· ⊤ )ijk, etc., mean that the individuals denoted by the indices belong to one doublet but are not all one individual.
3ℵi, 3ℵij, 3ℵijk, 3ℵijkl, mean that i, j, etc. all belong to the triplet ℵ.
3ijkl, 3ijklm, etc. mean that i, j, etc. all belong to one triplet.
(3· ⊤ )ijkl, means that i, j, k, l all belong to one triplet but are not all identical.
(3·2)ijkl means that i, j, k, l are three different existing individuals.
(32)ijklmnpq (where note the absence of a dot — not 3·2, but 32) means that the individuals indicated are all members of a triplet of doublets.
(3 2)ijklmno means that every individual denoted by an index is either a member of a triplet or of a doublet.
2)ijklmno means that every individual denoted by an index is either a member of a triplet or of a doublet.
I would use a special form of parenthesis (I will not recommend any particular form as more appropriate than another) which I would use in the following way:
Πi[⊙ |]i; means any object which is sun is, as such, the member of a singlet, i.e., ΠiΠj
|]i; means any object which is sun is, as such, the member of a singlet, i.e., ΠiΠj ⊙i
⊙i ⊙j
⊙j |ij.
|ij.
If ∫+ means is a satellite of Jupiter, then
Πi[∫+ 5]i; means that whatever is a satellite of Jupiter is, as such, a member of a quintuplet, i.e.,
5]i; means that whatever is a satellite of Jupiter is, as such, a member of a quintuplet, i.e.,
| ΣiΣjΣkΣlΣmΠn | ∫ +i· ∫ +j· ∫ +k· ∫ +l· ∫ +m· ⊤ ij· ⊤ ik· ⊤ il· ⊤ im |
| · ⊤ jk· ⊤ jl· ⊤ jm· ⊤ kl· ⊤ km· ⊤ lm·(~(∫ +n) | |
 |in |in |jn |jn |kn |kn |ln |ln |mn). |mn). |
The saving here is enormous.
Intimately connected with these abbreviations are others, some of which I have mentioned elsewhere. The rules of their application would form an elaborate logical doctrine, which I have not time to develop, because I am working at more fundamental parts of logic. Whoever undertakes it in the light of what I have said here and elsewhere will have other symbols forced upon his attention.
I pass to another and very simple abbreviation, which consists in using the symbol σ so that σij shall mean that j is at least as low an integer as i. That is,
(20) σij=Παs̄α q̄αiqαj q̄αiqαj |
σij=Σαsα·qαiq̄αj |
| It immediately follows that | |
| (21) | Πiσii and |
| (22) | ΠiΠjΠk σij σjkΨσik σjkΨσik |
| From (20) and (10) it follows that | |
| (23) | ΠiΠjΠk σijΨσjk σik σik |
(24) Πi|oi σoi σoi |
Πiσio |
The long formula (8) requires abbreviation; and we may write
| (25) Huv | = ΣαΠβΠγΠw sα·qαu·q̄αv·(s̄β q̄βu q̄βu qβw qβw s̄γ s̄γ qβv qβv q̄βw) q̄βw) |
| = Πwσuv·(σuwΨσwv) |
Formulæ (14)-(16) may be put in the form
| (14) ΠiΠjΠkΠuΠvΠw | σui σvj σvj ~(i+j)k ~(i+j)k ~(u+v)wΨσwk ~(u+v)wΨσwk |
| (15) ΠiΠjΠkΠuΠvΠw | σwk σvj σvj ~(i+j)k ~(i+j)k ~(u+v)wΨσui ~(u+v)wΨσui |
| (16) ΠiΠjΠkΠuΠvΠw | σui σwk σwk ~(i+j)k ~(i+j)k ~(u+v)wΨσvj ~(u+v)wΨσvj |
Putting, in (14), o for i, j, and w, it becomes
Multiplying this by the third power of (24), i.e., (24)·(24)·(24), we get
| (27) | (o+o)o |
(9) may be put in the form
| (9') | ΠαΠuΣvΠw | q̄αu qαv·(q̄αwΨσwv) qαv·(q̄αwΨσwv) |
| Putting for qα the expression σu, this becomes | ||
| (28) | ΠuΣvΠw | σuv·(σuwΨσwv) |
346. I will now return to addition. I will remark, by the way (for I do not make this paper at all systematic), that Schröder's notation  and
and 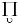 and the like, which is his chief modification of my two logical algebras (which, by the way, can perfectly well be mixed), made long after my second intentional section of the paper, No. XIII in vol. 3, has several advantages over mine, both theoretical and practical, and ought to be employed freely. But it fails to do what my invention was made in order to do, namely, to enable us to perform the operation of hypostatic abstraction, and freely make use of entia rationis. But that is neither here nor there.
and the like, which is his chief modification of my two logical algebras (which, by the way, can perfectly well be mixed), made long after my second intentional section of the paper, No. XIII in vol. 3, has several advantages over mine, both theoretical and practical, and ought to be employed freely. But it fails to do what my invention was made in order to do, namely, to enable us to perform the operation of hypostatic abstraction, and freely make use of entia rationis. But that is neither here nor there.
I will start with (14) in its last form and will trace out the steps of the algebraical transformation in closer detail than I purpose generally to do in this paper. For the inference I am coming to employs the Rule of Diduction, or diversification, which I fully treated of in a paper I drew up in Grammercy Park in 1885 †1, but the dignity of science does not permit me to go begging to have its results printed. This paper I am writing will probably never be seen by other eyes than those that see it written; but I record this for my own gratification. The rule is that after any quantifier of the Peircean (whether it be Π or Σ) can be inserted a Σ with a new index, into which the preceding index can be transmuted in any of the places where it occurs, remaining untransmuted in the other places. Thus Πilii everybody loves himself, can be changed to ΠiΣjlij, everybody loves somebody. Identifying v with j, in (14) we get
ΠiΠjΠkΠwΠu~(i+j)k σwk
σwk ~(u+j)w
~(u+j)w σui
σui
Let us insert the aggregant q̄βu:
ΠiΠjΠkΠwΠβΠu~(i+j)k σwk
σwk q̄βu
q̄βu ~(u+j)w
~(u+j)w σui
σui
The insertion of this aggregant authorizes the insertion of its negative as component of another aggregant.
ΠiΠjΠkΠwΠβΠu~(i+j)k σwk
σwk q̄βu
q̄βu ~(u+j)w
~(u+j)w qβu
qβu σui.
σui.
Let the index u now be diduced, becoming x in the last aggregant:
ΠiΠjΠkΠwΠβΠuΣx~(i+j)k σwk
σwk q̄βu
q̄βu ~(u+j)w
~(u+j)w qβx
qβx σxi.
σxi.
Let q̄αw be inserted as an aggregant:
ΠiΠjΠkΠαΠwΠβΠuΣx~(i+j)k q̄αw
q̄αw σwk
σwk q̄βu
q̄βu ~(u+j)w
~(u+j)w qβx
qβx σxi.
σxi.
The insertion of this aggregant authorizes the insertion of its negative as a component of another aggregant.
ΠiΠjΠkΠαΠwΠβΠuΣx~(i+j)k q̄αw
q̄αw σwk
σwk qαw·{q̄βu
qαw·{q̄βu ~(u+j)w}
~(u+j)w} qβx
qβx σxi.
σxi.
We now diduce w, transmuting it in one term into z, and thus obtain finally,
(29) ΠiΠjΠkΠαΠwΣzΠβΠuΣx~(i+j)k q̄αw
q̄αw σwk
σwk qαz·{q̄βu
qαz·{q̄βu ~(u+j)z}
~(u+j)z} qβx
qβx σxi.
σxi.
Here we have a nice little theoremidion, obvious though not self-evident. Namely, if any three positive integers, i, j, k, are such that k can result from adding i to j, then, selecting any class of integers we please, and speaking of the character of being an integer of this class as "the character α" either all integers of this class are as large as or larger than any integer k that can result from adding i to j, or else (if that is not the case) there is an integer of this class, z, if we take any second class of integers whatever (inclusion in which shall be called the character β) no integer u of this second class can on being added to j give the integer z, unless there be an integer x of the second class which is smaller than i. The form of statement is too strictly logical and formal for an ordinary mind readily to grasp it; but let us dilute it with a little verbiage, as follows. Suppose k is a positive integer which can result as the sum of j, as augend, and i, as addend. We select a first class of positive integers, say for example the cubes above 0 and 1. Now it may be that k does not exceed any of these. As to that case we say nothing. But should there be one or more of the first class that exceed k, then it may be that one of them is such that it cannot result from adding any positive integer to j as augend, because it may be less than j. It would have been better if, instead of writing ΣzΠβΠu in the Peircean, I had written ΠβΠuΣz for it is always allowable to carry Σ's to the right. Then the second class being selected first, it might happen that there was an integer of the first class that could not result from adding any integer of the second class to j. . . .






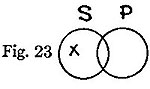
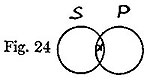
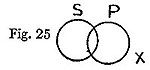
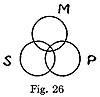
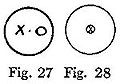
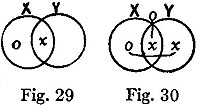
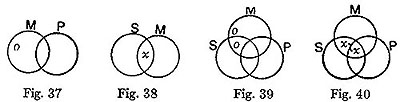
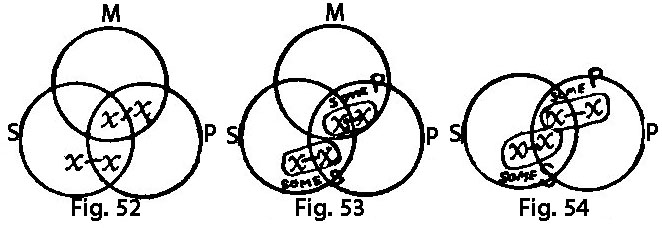
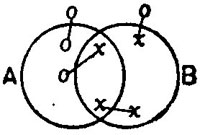
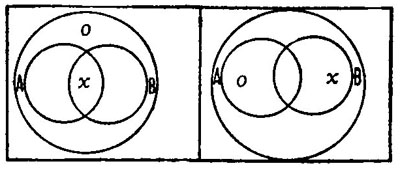
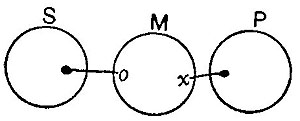
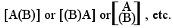
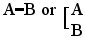
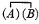
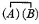
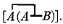
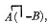
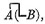
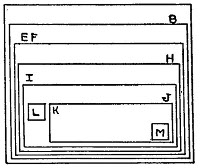
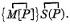
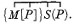
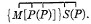
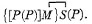
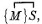
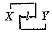
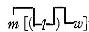
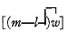
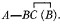
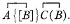
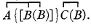
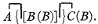
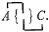
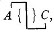
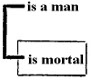
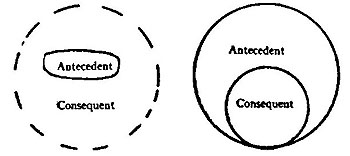
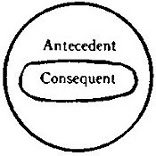
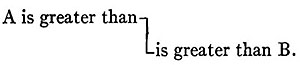







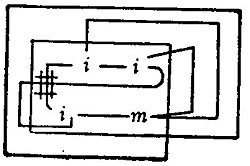
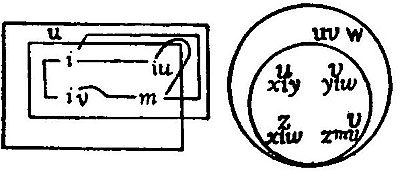
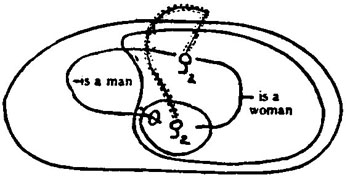
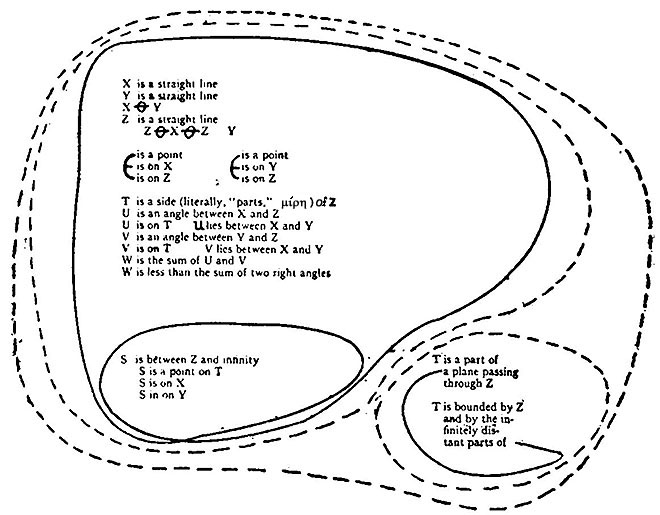
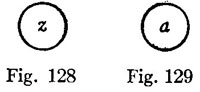
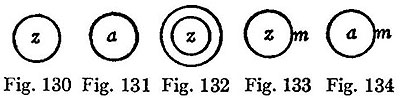
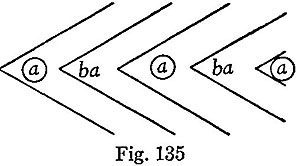
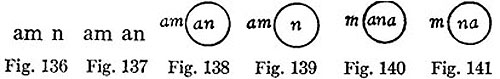
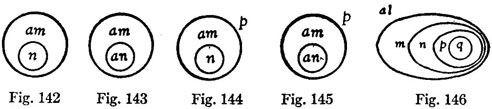
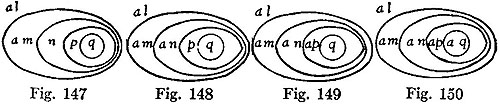
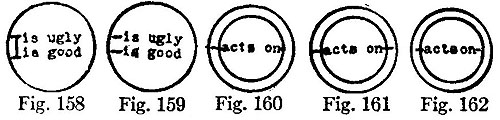






-.jpg)